1.树的定义和树的存储结构

主要根据https://subingwen.cn/data-structure/ 进行学习

1.树的定义

1.1定义

树（Tree）是n（n>=0）个节点的有限集。当n=0时称为空树。

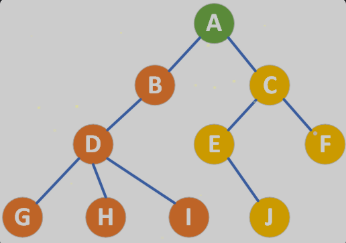
对于上面这棵树而言，A是它的根节点，左侧橙色部分和右侧黄色部分分别是这棵树的两个子树，而分别在以B、C为根节点的子树中还有子树，所以我们可以说树是递归定义的，树的特性对于它们的子树以及子树的子树而言同样是适用的。

1.2节点的关系和分类

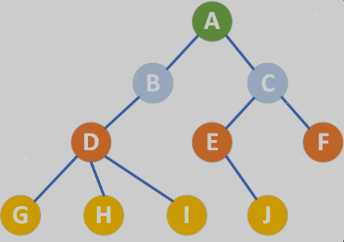
1. 节点（Node）：树中的每个元素称为节点，即图中的A、B、C、...、H、I、J。
2. 根节点（Root Node）：树的顶层节点，没有父节点，即图中的节点A。
3. 父节点（Parent Node）：直接连接某个节点的上层节点。比如:

• B、C节点的父节点为根节点A
• E、F节点的父节点为节点C
• G、H、I节点的父节点为根节点D

4. 子节点（Child Node）：由某个节点直接连接的下层节点。比如:

• A节点的子节点为节点B、C
• C节点的子节点为节点E、F
• D节点的子节点为节点G、H、I

5. 子孙节点：以某节点为根的子树中的任意节点都是该节点的子孙
6. 叶子节点（Leaf Node）：没有子节点的节点。图中的G、H、I、J就是叶子节点。
7. 兄弟节点（Sibling Nodes）：具有相同父节点的节点。
8. 堂兄弟节点：在树中的层次相同，但是父节点不同。举例：

• 节点D和节点E、F互为堂兄弟节点
• 节点G、H、I和节点、J互为堂兄弟节点

9. 层次（Level）：从根开始定义，根为第一层，根的孩子为第二层，以此类推。图中相同颜色的节点表示相同的层次，从根节点向下一共四层。
10. 路径（Path）：从一个节点到另一个节点所经过的节点序列。
11. 高度（Height）：节点到叶节点的最长路径长度。

• 从根节点到叶子节点得到的高度就是树的高度
• 根节点A到叶子节点F的高度是3，到叶子节点G、H、I、J的高度是4，所以根节点的高度是4，树的高度也是4

12. 深度（Depth）：节点到根节点的路径长度。比如：

• 从A到E深度为3，从A到H深度为4

13. 子树（Subtree）：由一个节点及其所有后代节点组成的树。
14. 度（Degree）：节点的子节点数量，树的度是所有节点度的最大值。

• 叶子节点的度为0
• 树的度是树内各个节点度的最大值
• 节点E的度为1，节点A的度为2，节点D的度为3，树的度为3

15. 有序树/无序树：如果树以及它的子树中所有子节点从左至右是有次序的，不能互换的，此时将这棵树称为有序树，否则称为无序树。
16. 森林（Forest）：m（m>=0）棵互不相交的树的集合。

2.树的存储结构

在数据结构中，树的表示法有多种，常见的包括双亲表示法、孩子表示法和孩子兄弟表示法。

2.1双亲表示法

双亲表示法是一种用数组来表示树的方法，在存储树节点的时候，在每个节点中附设一个指示器指示其双亲节点在数组中的位置。

struct TreeNode
{
    int data;
    int parent;
};

• data：节点存储的数据
• parent：父节点在数组中的位置，根节点没有父节点，用 -1 表示
  
  
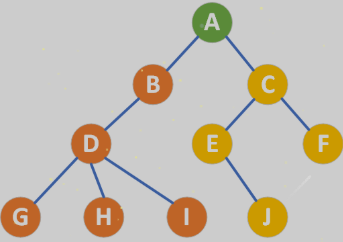
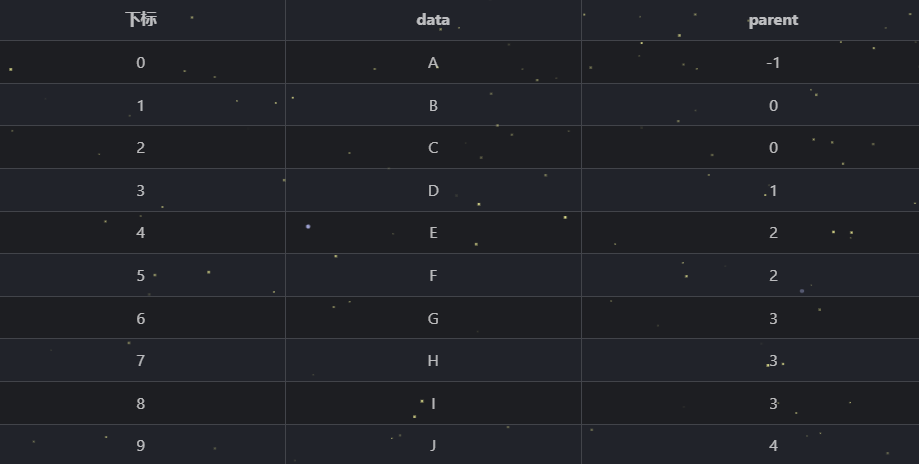
  但是如果我们想知道当前节点的子节点是谁，就需要遍历整棵树才能得到结果。
  如果我们对上面的TreeNode结构进行优化给它添加用于描述孩子节点位置的成员就可以快速找到当前节点的子节点了:

struct TreeNode
{
    int data;
    int parent;
    int child1;
    int child2;
        ...
        ...
        ...
};

但是此时问题来了，对于一棵树中的节点而言，我怎么知道它有多少个子节点呢？如果child成员定义的太多会浪费存储空间，如果定义的太少就不能存储所有的子节点信息。这该如何是好呢？

2.2.1孩子表示法

孩子表示法是一种为每个节点存储其所有子节点的表示方法，在存储的时候可以使用数组也可以使用链表。
孩子表示法中，每个节点都有一个指针列表或数组，指向它的所有子节点。我们可以使用 std::vector 来存储子节点指针。关于节点结构可以这样定义：

struct TreeNode 
{
    int value; 
    std::vector<TreeNode*> children;
};

• value：节点的值，可以根据实际需求修改为其他数据类型
• children：子节点列表，存储的是当前节点所有的子节点
  通过这种方式能够非常轻松的基于父节点找到它所有的子节点，但是想要通过子节点访问其父节点就变得麻烦了。

2.2.2孩子双亲表示法

struct TreeNode 
{
    int value; 
    TreeNode* parent;
    std::vector<TreeNode*> children;
};

• value：节点的值，可以根据实际需求修改为其他数据类型
• parent：记录当前节点的父节点的位置（地址）。
• children：子节点列表，存储的是当前节点所有的子节点
  做了这样的修改之后，可以在程序中再添加一个setParent方法，用于给各个节点设置父节点（根节点的父节点可以指定为 nullptr）

2.3孩子兄弟表示法

在孩子兄弟表示法中，树被转化为了一种特殊的树，我们可以做这样的约定：每个节点的左侧子节点表示该节点的第一个子节点，而右侧子节点表示该节点的下一个兄弟节点。也就是说在内存中这棵树的存储结构和实际的逻辑结构是不一样的。

struct TreeNode 
{
    int value;
    TreeNode* firstChild; 
    TreeNode* nextSibling; 
};

• value：节点的值，可以根据实际需求修改为其他数据类型
• firstChild：指向第一个子节点（地址）
• nextSibling：指向下一个兄弟节点（地址）
  
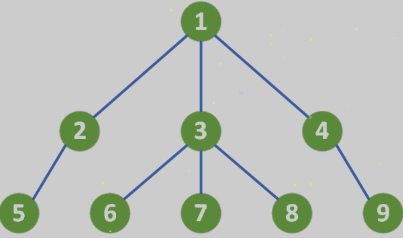
  如果想要在内存中存储这样的一棵树，我们需要使用孩子兄弟表示法对其进行转换可以得到下面这个图：
  
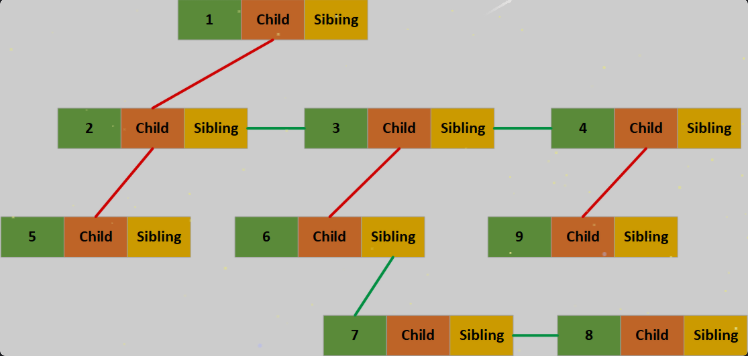
  在上面的图中红色线表示节点之间的关系为父子，绿色的线表示节点之间的关系为兄弟，但是这样看起来似乎还是不太直观，我们来换一种画法：
  
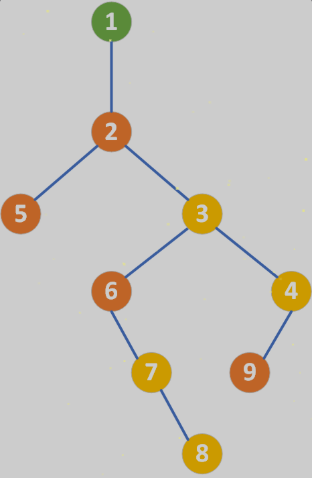
  图中的左侧节点（橙色）表示和父节点之间原来的实际关系为父子，右侧节点（黄色）表示节点和父节点之间原来的实际关系为兄弟。