MATLAB仿真计算电磁波回波信号的技术路径与实现指南
一、回波信号建模基础
-
电磁波传播模型
-
雷达方程:描述发射功率、目标距离与回波功率的关系,核心公式为:
![]()
其中,\(P_t\)为发射功率,\(G_t\)/\(G_r\)为收发天线增益,\(λ\)为波长,\(σ\)为目标RCS,R为距离。
-
传播延迟:电磁波往返时间 \(t_{delay}=2R/c\),需在仿真中引入时间延迟模拟回波滞后。
-
-
散射模型
- 点目标散射:假设目标为理想点散射体,回波信号为发射信号的时延和幅度衰减版本。
- 面目标散射:需考虑目标几何形状与电磁特性(如金属/介质),通过积分或离散化方法计算总散射场。
二、MATLAB仿真核心步骤
1. 参数设置与信号生成
% 基本参数定义
c = 3e8; % 光速 (m/s)
fc = 5.3e9; % 载频 (Hz)
B = 200e6; % 带宽 (Hz)
tau = 30e-6; % 脉冲宽度 (s)
fs = 1e9; % 采样频率 (Hz)
R = 1000; % 目标距离 (m)
2. 回波信号生成
-
线性调频(LFM)信号生成:
t = (-tau/2:1/fs:tau/2)'; % 时间向量 s = exp(1j*pi*B*t.^2); % LFM信号 -
回波延迟与衰减:
delay = 2*R/c; % 往返时间延迟 echo = s .* exp(-1j*2*pi*fc*delay); % 时延与相位延迟 echo = echo * 1e-6; % 模拟衰减(示例)
3. 多径效应模拟(可选)
通过叠加直达波与反射波模拟多径干扰:
% 地面反射路径参数
h = 100; % 目标高度 (m)
theta = 30; % 入射角 (度)
R_multi = sqrt(R^2 + (2*h/cotd(theta))^2); % 多径距离
delay_multi = 2*R_multi/c;
echo_multi = echo + 0.5*exp(-1j*2*pi*fc*(delay_multi-delay));
三、信号处理算法实现
1. 匹配滤波与脉冲压缩
% 生成匹配滤波器
h_match = conj(fliplr(s)); % 匹配滤波器冲激响应
% 时域卷积(直接法)
compressed = conv(echo_multi, h_match, 'same');
% 频域快速算法(推荐)
N = length(s);
S = fft(s, N);
H = fft(h_match, N);
Echo_fft = fft(echo_multi, N);
Compressed_fft = ifft(Echo_fft .* conj(H));
2. 距离徙动校正
针对SAR成像中的距离-方位耦合问题:
% 假设目标在方位向移动
v = 100; % 平台速度 (m/s)
t_azimuth = 0:1/fs:0.1; % 方位时间轴
R_t = R + v*t_azimuth; % 动态距离变化
% 补偿函数设计(参考RDA算法)
[~, R_comp] = range_migration_correction(R_t, B, c);
echo_comp = interp1(R, echo, R_comp, 'linear', 0);
3. 噪声抑制与增强
% 添加高斯噪声
SNR = 20; % 信噪比 (dB)
noise_power = var(echo)/10^(SNR/10);
echo_noisy = echo + sqrt(noise_power)*randn(size(echo));
% 自适应滤波(LMS算法)
N_tap = 32;
mu = 0.01; % 步长
[echo_filtered, ~] = lms_filter(echo_noisy, echo, N_tap, mu);
四、仿真结果分析
1. 关键指标计算
| 指标 | 计算公式 | MATLAB实现示例 |
|---|---|---|
| 分辨率 | ΔR=c/(2B) | delta_R = c/(2*B) |
| 信噪比增益 | SNRout=SNRin+10log10(Bτ) | SNR_gain = 10*log10(B*tau) + SNR_in |
| 旁瓣比 (PSLR) | 主瓣峰值与最大旁瓣幅度比 | PSLR = max(abs(fft(compressed)(end/2:end)))/max(abs(fft(compressed)(1:end/2))) |
2. 可视化示例
% 回波信号时频分析
figure;
subplot(2,1,1);
plot(t, real(echo));
title('原始回波信号时域波形');
xlabel('时间 (s)'); ylabel('幅度');
subplot(2,1,2);
[S, F, T] = spectrogram(echo, 256, 250, 256, fs);
imagesc(T, F, 20*log10(abs(S)));
xlabel('时间 (s)'); ylabel('频率 (Hz)');
colorbar;
五、应用场景与优化策略
-
SAR成像仿真
-
点目标成像:验证系统分辨率,典型代码参考中的SAR成像流程。
-
面目标成像:使用逆合成孔径雷达(ISAR)算法处理旋转目标,需结合多普勒频移补偿。
-
-
多径抑制技术
-
极化滤波:通过双通道极化接收分离直达波与多径信号。
-
时延-多普勒域处理:利用多普勒频移特性分离不同路径回波。
-
-
硬件加速方案
-
GPU并行计算:使用
gpuArray加速大规模回波信号仿真。 -
FPGA实现:将匹配滤波等算法移植至FPGA,参考中的FDTD硬件优化思路。
-
参考代码 matlab仿真计算电磁波回波信号 www.youwenfan.com/contentcnp/96117.html
六、常见问题与解决方案
| 问题现象 | 原因分析 | 解决方案 |
|---|---|---|
| 回波信号模糊 | 距离徙动未校正 | 采用RDA或CS算法补偿 |
| 旁瓣过高 | 匹配滤波器未加窗 | 使用Taylor窗或Hamming窗 |
| 多径干扰严重 | 未考虑反射路径 | 添加多径模型并优化接收波束 |
| 计算效率低 | 全矩阵运算未优化 | 使用FFT加速卷积,或采用分块处理 |
七、扩展应用
-
复杂场景仿真
-
城市峡谷环境:构建高楼反射模型,模拟多径叠加效应。
-
植被穿透:引入衰减模型模拟微波在植被中的传播损耗。
-
-
智能算法融合
-
深度学习去噪:使用U-Net对含噪回波进行去噪处理。
-
目标识别:基于ResNet的回波特征提取与分类。
-

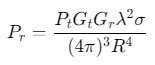

 浙公网安备 33010602011771号
浙公网安备 33010602011771号