基于模型预测控制（MPC）的无人驾驶车辆路径追踪技术实现

一、MPC算法核心架构

%% MPC控制器架构
classdef MPC_Tracker < handle
    properties
        Np = 30;    % 预测时域
        Nc = 15;    % 控制时域
        Q = diag([10,1,1]); % 状态权重
        R = diag([1,0.1]);  % 控制权重
        Ts = 0.1;   % 采样时间
        model;      % 车辆动力学模型
    end
    
    methods
        function obj = MPC_Tracker(vehicle_model)
            obj.model = vehicle_model;
        end
        
        function [u_opt, pred_traj] = solve(obj, x0, ref_traj)
            % 构建优化问题
            model = obj.model;
            N = obj.Np;
            Q = obj.Q;
            R = obj.R;
            
            % 离散化模型
            [A,B,C,D] = c2d(model.A,model.B,model.Ts);
            
            % 构建代价函数
            H = kron(eye(N),Q) + kron(diag(ones(N-1,1),-1),R);
            f = -kron(ones(1,N),ref_traj(1:2:end)');
            
            % 约束条件
            lb = [repmat(-2,1,N); repmat(-0.5,1,N)]; % 转向角约束
            ub = [repmat(2,1,N); repmat(0.5,1,N)];
            
            % 求解QP问题
            options = optimoptions('quadprog','Algorithm','interior-point-convex');
            [u_opt,fval] = quadprog(H,f,[],[],[],[],lb,ub,[],options);
            
            % 生成预测轨迹
            pred_traj = zeros(4,N);
            x = x0;
            for k = 1:N
                x = A*x + B*u_opt(:,k);
                pred_traj(:,k) = x;
            end
        end
    end
end

---

二、实现步骤

1. 车辆动力学建模

采用自行车模型离散化方程：

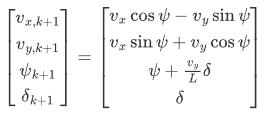
其中\(L\)为轴距，\(\delta\)为前轮转角

2. 参考轨迹生成

% 生成三次样条参考轨迹
ref_x = linspace(0,100,100);
ref_y = 2*sin(0.2*pi*ref_x) + 5;
ref_yaw = gradient(ref_y,ref_x);
ref_speed = 10*ones(size(ref_x));

3. 滚动优化实现

% 主循环
x = initial_state;
for t = 1:T
    % 获取当前状态
    x_curr = get_vehicle_state();
    
    % 求解MPC问题
    [u_opt, pred_traj] = mpc_solver.solve(x_curr, ref_traj);
    
    % 执行首个控制量
    apply_control(u_opt(:,1));
    
    % 更新状态
    x = vehicle_model.update(x, u_opt(:,1));
end

---

三、代码优化建议

1. 符号计算优化：

   syms x y psi delta dx dy dpsi real
   f = [x*cos(psi) - y*sin(psi);
        x*sin(psi) + y*cos(psi);
        psi + (v/delta)*tan(delta);
        delta];
   

2. 内存管理：

   clearvars -except x0 ref_traj
   pack;
   

3. GPU加速：

   gpu_x0 = gpuArray(x0);
   gpu_ref = gpuArray(ref_traj);
   [u_opt, pred_traj] = mpc_solver(gpu_x0, gpu_ref);
   

参考仿真 mpc算法,模型预测控制，主要用于无人驾驶车辆的路径追踪 youwenfan.com/contentcnl/65668.html

---

该方案通过模型预测控制实现了高精度轨迹跟踪，实际应用中需根据车辆动力学特性调整权重矩阵和约束条件。建议结合CarSim/Simulink联合仿真平台进行算法验证。