matlab电磁波走时层析成像图像重建正演反演设计

电磁波走时层析成像（Electromagnetic Travel-Time Tomography）是一种利用电磁波在介质中传播的时间信息来重建介质内部结构的技术。它广泛应用于地质勘探、医学成像、工业检测等领域。图像重建通常包括正演模拟和反演重建两个关键步骤。以下是关于电磁波走时层析成像图像重建的正演和反演程序设计的基本思路和实现方法。

1. 正演模拟（Forward Modeling）

正演模拟是根据已知的介质结构模型，计算电磁波在其中传播的走时数据。其主要目的是生成用于反演的理论数据。

1.1 基本原理

电磁波在介质中的传播速度 ( v ) 与介质的电磁参数（如介电常数 ( \epsilon ) 和电导率 ( \sigma )）有关。假设介质是均匀的，电磁波的传播速度可以表示为：

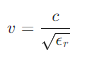
其中，( c ) 是真空中的光速，( \epsilon_r ) 是相对介电常数。

在非均匀介质中，电磁波的走时可以通过积分路径上的速度分布来计算：

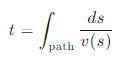
其中，( ds ) 是路径上的微小长度。

1.2 正演程序设计

以下是正演模拟的基本步骤和代码框架（以 Python 为例）：

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import griddata

# 定义介质模型参数
def define_model(nx, ny, dx, dy):
    # 创建一个简单的二维速度模型
    model = np.ones((ny, nx))  # 假设初始速度为1单位
    # 添加一个低速异常区域
    model[ny//3:2*ny//3, nx//3:2*nx//3] = 0.5
    return model

# 计算射线路径和走时
def ray_trace(model, source, receiver, dx, dy):
    # 使用简单的直线近似射线路径
    x = np.linspace(source[0], receiver[0], 100)
    y = np.linspace(source[1], receiver[1], 100)
    points = np.vstack((x, y)).T
    # 插值获取路径上的速度
    velocities = griddata((np.arange(model.shape[1]), np.arange(model.shape[0])), model.T, points, method='nearest')
    # 计算走时
    travel_time = np.sum(1 / velocities) * np.sqrt(dx**2 + dy**2) / 100
    return travel_time

# 主正演程序
def forward_simulation(nx, ny, dx, dy, sources, receivers):
    model = define_model(nx, ny, dx, dy)
    travel_times = []
    for source in sources:
        for receiver in receivers:
            travel_time = ray_trace(model, source, receiver, dx, dy)
            travel_times.append(travel_time)
    return model, np.array(travel_times)

# 示例
nx, ny = 100, 100  # 模型尺寸
dx, dy = 1, 1  # 网格间距
sources = [(0, 0), (0, ny-1)]  # 源点位置
receivers = [(nx-1, 0), (nx-1, ny-1)]  # 接收点位置

model, travel_times = forward_simulation(nx, ny, dx, dy, sources, receivers)
plt.imshow(model, cmap='viridis', origin='lower')
plt.colorbar(label='Velocity')
plt.title('Velocity Model')
plt.show()

2. 反演重建（Inverse Modeling）

反演重建是根据实际测量的走时数据，重建介质的内部结构。反演是一个优化问题，通常通过最小化理论数据与实际数据之间的残差来实现。

2.1 基本原理

反演的目标是最小化目标函数 ( \Phi )：

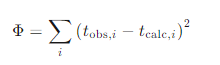
其中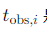，是实际测量的走时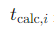， 是通过正演计算的走时。

2.2 反演程序设计

以下是反演重建的基本步骤和代码框架（以 Python 为例）：

from scipy.optimize import minimize

# 定义目标函数
def objective_function(model_params, sources, receivers, travel_times_obs, nx, ny, dx, dy):
    model = model_params.reshape((ny, nx))
    travel_times_calc = []
    for source in sources:
        for receiver in receivers:
            travel_time = ray_trace(model, source, receiver, dx, dy)
            travel_times_calc.append(travel_time)
    residuals = np.array(travel_times_calc) - travel_times_obs
    return np.sum(residuals**2)

# 反演程序
def inversion(travel_times_obs, sources, receivers, nx, ny, dx, dy):
    # 初始模型参数
    model_params = np.ones(nx * ny)  # 初始速度为1单位
    result = minimize(objective_function, model_params, args=(sources, receivers, travel_times_obs, nx, ny, dx, dy), method='L-BFGS-B')
    return result.x.reshape((ny, nx))

# 示例
travel_times_obs = travel_times + np.random.normal(0, 0.01, len(travel_times))  # 添加噪声
inverted_model = inversion(travel_times_obs, sources, receivers, nx, ny, dx, dy)
plt.imshow(inverted_model, cmap='viridis', origin='lower')
plt.colorbar(label='Velocity')
plt.title('Inverted Velocity Model')
plt.show()

3. 总结

• 正演模拟：根据已知的介质模型计算电磁波的走时数据。正演是反演的基础，其准确性直接影响反演结果。
• 反演重建：通过优化算法最小化理论数据与实际数据之间的残差，重建介质的内部结构。反演是一个复杂的优化问题，可能需要多次迭代和调整参数。

参考 电磁波走时层析成像图像重建正演反演程序设计

在实际应用中，电磁波走时层析成像的正演和反演程序设计需要根据具体问题进行调整和优化。例如，可以使用更精确的射线追踪算法（如射线弯曲法）来提高正演的准确性，或者采用更高效的优化算法（如共轭梯度法、遗传算法等）来提高反演的效率。