IOI 2026 中国国家集训队作业（试题泛做）记录

跟着学长做。可能不是很详细。

qoj1875 Nein

link

qoj970 Best Subsequence

考虑单次询问怎么做。二分，设 \(\le W\) 的为一类数，其余为二类数，显然二类数不能相邻，则肯定有一种最优解满足一类数全选了（考虑贪心调整，不证）。复杂度 \(\mathcal{O}(n \log n)\)。

定义答案相邻的一类数，二类数，一类数为一个三元组 \((a, b, c)\)，则对于所有 \(i = c\)，\(b\) 一定是弹出去的单调栈上的元素之一且 \(a\) 一定是在单调栈上在 \(b\) 前面一个的元素。自证不难。则总的三元组个数是 \(\mathcal{O}(n)\) 的。

又，对于每一个可能的一类数和三元组，他们都对应答案中的一个 \(1\)，且都有一个使它存在的 \(W\) 的区间下界 \(W'\)，则我们可以考虑把它放到主席树上维护，二分时求一下区间 \(\le W\) 的数的个数即可（注意它是一个环，所以还要考虑两边的情况）。

代码。

qoj1884 Mission Impossible: Grand Theft Auto

先把二度点缩掉。考虑随便定一个非叶子节点为根，将叶子按 dfn 序排序，则有一种覆盖方式就是以某个叶子 \(x\) 为起点，依次覆盖 \((x, x + 1), (x - 1, x + 2), \dots\)

但是，我们发现这样做会有一个问题，就是可能在覆盖的中途漏掉一些边。我们称漏掉的边为 bad 边：

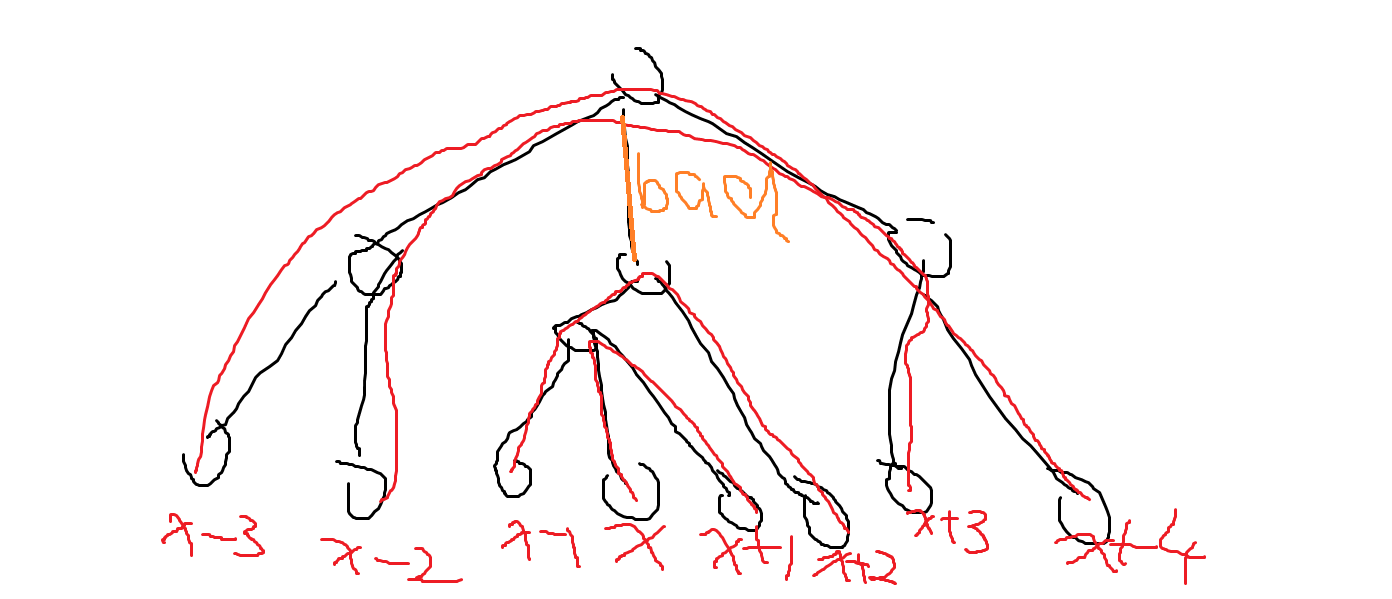
（偷个图，来源）

那你可能会说，直接在覆盖完 bad 边的子树后覆盖一下 bad 边不就行了。但是，需要注意的是 \(x\) 的 bad 边可能有多个，你直接这么搞可能次数就超了。

定义一条边对一个点贡献一次，当且仅当以那个点为起点时，这条边是 bad 边。显然，一条边贡献到的点一定为子树内的中间叶子和子树外的中间叶子（能贡献到当且仅当子树内/外的叶子个数是偶数），且贡献数不超过 \(2\)（可以看图揣摩一下）。

我们发现由于二度点都被缩掉了，则这颗树的总边数不会超过 \(2m - 2\)。分两种情况讨论。

• \(m\) 是偶数：

显然，每个叶子向上连的边一定不会贡献到任何一个节点，剩下的 \(m - 2\) 条边每条边最多贡献 \(2\) 次，总贡献数不超过 \(2x - 4\)，则必有一个节点被贡献到的次数 \(\le 1\)，取这个点为起点即可。

• \(m\) 是奇数：

此时由于 \(m\) 是奇数，每条边必定会贡献恰好 \(1\) 次。同上文的分析，取被贡献次数 \(1\) 的点为起点即可。

此时，由于所有叶子向上连的边贡献到的点恰好是所有叶子，则此时的 bad 边一定是最后剩下的叶子向上连的边。直接在构造的最后把那个叶子和根覆盖即可。

直接按上面的方法构造即可，复杂度 \(\mathcal{O}(n)\)。

代码（tip：写代码时甚至不需要刻意把二度点缩掉）

qoj2610 Build a City

link

qoj2601 Lucky Tickets

逆天数学题。不会证，咕咕咕。代码。

qoj2605 Soccer Match

神秘 ad-hoc。

考虑先随机一种染色方案，使得异色的边数 \(\ge \lceil \frac{m}{2} \rceil\)。如果小于它，那么每次找到所有点，使得与他相连的同色边个数大于异色边，并将其颜色翻转。

此时异色边数 \(\ge \lceil \frac{m}{2} \rceil \ge kn\)。如果有一个点的异色边 \(\le k\)，就把这个点删掉。可以发现在任意时刻，异色边数永远 \(\ge kn\)，则最后的方案一定有至少两个异色点，一定满足题意。

考虑证明为什么上面随机方案后复杂度是对的。根据计算可以得知，异色边的均值为 \(\mu = \frac{m}{2}\)，方差为 \(\sigma^2 = \frac{m}{4}\)。设开始共进行了 \(a\) 轮翻转，则一开始的异色边数最多 \(\lceil \frac{m}{2} \rceil - a\)，由切比雪夫不等式，有 \(P(x \le \mu - a) \le \frac{\sigma^2}{a^2}\)。则对于 \(a = c \sqrt m\)，该事件发生的概率不超过 \(\frac{1}{4c^2}\)，故对于绝大多数情况，\(a\) 是 \(\mathcal{O}(\sqrt m)\) 量级的，复杂度即为 \(\mathcal{O}(n \sqrt m)\)。

代码。

qoj4878 Easy Problem

考虑单次询问怎么做。这种问题就相当于一个二分图匹配，所以我们可以考虑 hall 定理。但是直接 hall 不太可以从前一个位置转移到后一个，思考所有区间都包含 \(i\) 的性质有什么用。

突破口：设第 \(j\) 个喂食器分别给左右两边喂了 \(lc_j, rc_j\)。则左右两边的答案就分别是 \(L = \min\limits_{1 \le p \le x}\{\sum\limits_{k = p}^{x - 1} a_k + \sum\limits_{l_j < p} lc_j\}\) 和 \(R = \min\limits_{x - 1 \le p \le n}\{\sum\limits_{k = x}^p a_k + \sum\limits_{r_j > p} rc_j\}\)。

初始设 \(lc_j = 0\)，\(rc_j = c_j\)。可以进行贪心，考虑在不减小 \(R\) 的情况下尽可能的增加 \(L\)。则设 \(p\) 为 \(R\) 取到最小值的最左边的位置，然后找出 \(r_j \le p\) 的所有 \(l_j\) 最小的区间 \(j'\)。我们尽量将 \(rc_{j'}\) 减小，直到最小值位置前移，或 \(rc_{j'} = 0\) 为止。持续进行这样的贪心直到没有区间可以选，则此时的答案最大（证明：咕咕咕）。

当 \(i \to i + 1\) 时，会删除 \(r_j = i\) 的区间，并加入 \(l_j = i + 1\) 的区间。发现这些区间的增减都不会影响上述的贪心，则直接在上面的基础上继续贪就行了。以上所述操作均可以使用线段树。

至于贪心为什么复杂度是对的，定义势能为 \(R\) 的那颗线段树上左儿子最小值大于右儿子个数，则一次操作要么把一个 \(rc\) 变成 \(0\)，要么至少使势能减小 \(1\)。而加入一个区间增加的势能是 \(\mathcal{O}(\log n)\) 级别的，则总复杂度为 \(\mathcal{O}((n + m)\log^2 n)\)。

代码。原来的代码获得了最长解

qoj4786 Balance

容易发现一组解 \(x\) 一定存在两个长为 \(n\) 的序列 \(p\) 和 \(q\)，使得 \(x_{i, j} = p_i + q_j\)。则我们就是要使 \(n \sum\limits_{i = 1}^n (p_i + q_i)\) 最小。发现对于任意一个排列 \(c\)，\(\sum\limits_{i = 1}^n a_{i, c_i} \le \sum\limits_{i = 1}^n (p_i + q_i)\)。

这个玩意就是二分图最大权完美匹配，考虑直接跑最大费用最大流。由于有 \(dis_{r(j)} \ge dis_{l(j)} + a_{i, j}\)，则直接将 \(p_i \to -dis_{l(j)}\)，\(q_i \to dis_{r(j)}\) 就是满足条件的最小解。

代码。

qoj4884 Battleship: New Rules

发现长条之间点变不叫比较难搞。考虑把他变成要在 \((n + 1) \times (n + 1)\) 的方格内填长或宽为 \(2\) 的长方形使得覆盖的尽量多，允许相交，最终的构造就是把长方形右侧和下侧全部挖掉。

则容易发现 \(n\) 为奇数时，一定能填满，则直接输出 \(-1\) 即可。

当 \(n\) 为偶数时，发现此时一定会有一个空位，而空位的左上方就是答案。

考虑分治，每次找一个分界线，然后询问分界线上的所有点。如果是 \(1\)，则说明以这个位置为左上角的 \(2 \times 2\) 的一个小矩形都被覆盖了，把它们都标记一下。如询问完之后，有一边未标记的格子个数为奇数，则答案一定在那一侧，次数为 \(\mathcal{O}(n \log n)\)。如改为将长的那一边分治割一般，则次数为 \(\mathcal{O}(n)\) 的。

代码。

qoj4788 Gravity

把连通块按掉下去所需的时间从小到大排序，每次找到最先下落的连通块，把他落下去，然后更新他上方连通块的时间。随便搞一下就行了，复杂度 \(\mathcal{O}(nm \log nm)\)，注意不要写假。

代码。我不会告诉你我使用了 set 获得了最劣解和最长解

qoj6540 Beautiful Sequence

设最终答案中满足 \(a_{i - 1} \le a_i \ge a_{i + 1}\) 的数为 \(A\) 集合的数，其余为 \(B\) 集合的数，则我们就是要使 \(|B|\) 最小。容易发现连续的 \(A\) 集合的数都相等。

将原数组排序后去重后设为 \(b_1 < b_2 < \dots < b_m\)，出现次数为 \(c_1, c_2, \dots, c_m\)。首先我们可以将 \(b_m\) 忽略，则相当于我们要对每一个 \(A\) 的连续段分配一个小于等于他的 \(B\) 的数。

考虑贪心，维护一个小根堆，表示 \(A\) 的集合。再记录一个 \(r\) 表示前面留下的未匹配的 \(B\) 集合的个数。从小到大枚举 \(b\)：

• 如 \(r > 0\)：

将 \(r\) 减 \(1\)，代表将一个没有匹配的 \(B\) 集合元素跟 \(b\) 匹配。

• 如 \(r = 0\)：

设小根堆堆顶为 \(x\)。弹出小根堆堆顶，并将 \(x - 1\) 加入（如 \(x > 1\)），表示将那个大小为 \(x\) 的连续段抽出一个来跟目前的连续段匹配。特别的，当 \(x = 1\) 时，要将 \(r\) 增加 \(1\)，因为跟它匹配的那个数就空出来可以和后面的连续段匹配了。

证明咕咕咕，但是感性理解一下看起来就很对。最终答案就是 \(n\) 减去第二次操作的次数。

代码。