关于反射容斥
骗你的。
本文术语运用可能不规范,轻喷。
\(\text{Part 0}\)
Q:只能向右或向上走,从 \((0, 0)\) 走到 \((n, m)\) 有多少种方案?
A:\(\binom{n + m}{n}\)。小学奥数,不讲。
\(\text{Part 1}\)
Q:跟上面一样,但要求路径不能与直线 \(y = x + b\) 相交。
A:考虑 \((n, m)\) 关于此直线的对称点 \((p, q)\),让我们画个图。
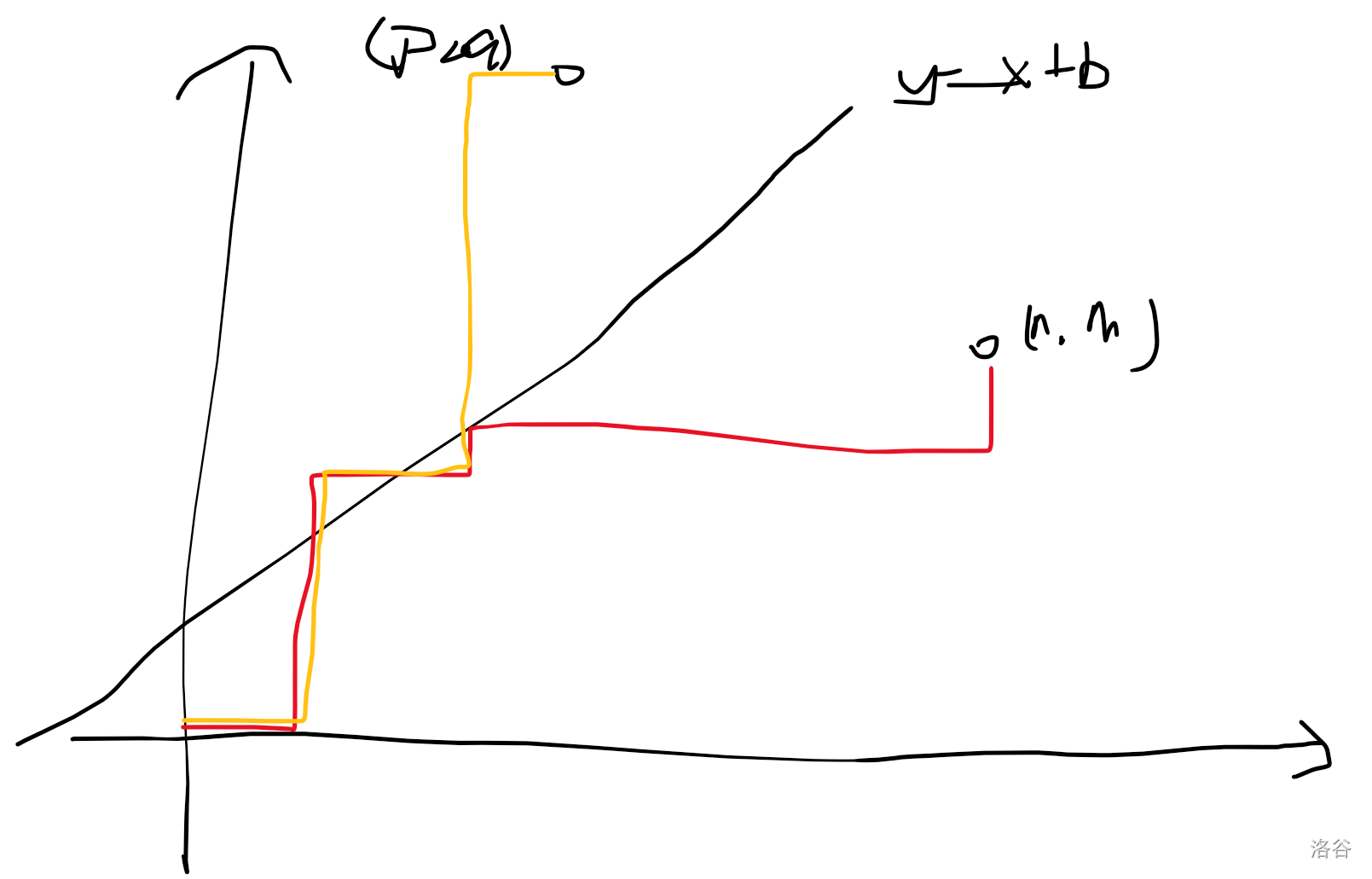
我们可以观察到,每一条不符合条件的路径与所有 \((0, 0)\) 走到 \((p, q)\) 的路径构成了一个双射。
则答案为 \(\binom{n + m}{n} - \binom{p + q}{p}\)。
\(\text{Part 2}\)
Q:跟上面一样,但同时要求路径不能与另外一条直线 \(y = x + b'\) 相交。
A:将路径表示成跟两条直线相交的点的有序序列,如 \(AABBA\)。发现与某一条直线连续相交没有什么影响,则将其转化成 \(ABA\) 的形式。
对于 \(S\) 为路径序列的子序列的答案 \(f(S)\),类似于上面的推导,将 \((n, m)\) 按照这个序列的顺序对称若干次,每一次对称将 \((n, m)\) 和另外一条线同时关于当前的线对称,设对称完之后的点是 \((p, q)\),则答案就是 \(\binom{p + q}{p}\)(需要保证 \((p, q)\) 没有飞到其他象限)。
类似于这样(以 \(AB\) 改的):
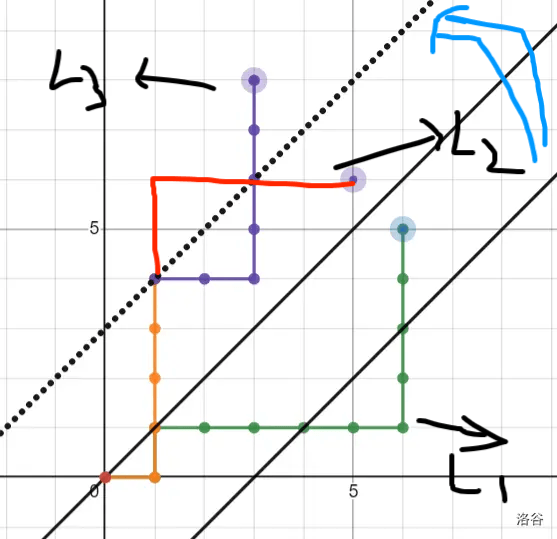
其中蓝点是初始点 \((n, m)\),紫点是最终点 \((p, q)\)。从图中可以路径 \(L1\) 和 \(L2\) 是一对映射,\(L2\) 和 \(L3\) 是一对映射,则 \(L1\) 和 \(L3\) 也是一堆映射,一个 \((0, 0)\) 到 \((p, q)\) 的路径恰好对应一个 \(AB\) 的方案。
这样的话,我们考虑容斥,则答案为 \(∅ - f(A) - f(B) + f(AB) + f(BA) - \dots\),复杂度可以看作 \(\mathcal{O}(n + m)\)。
这就是反射容斥。
\(\text{Part 3.}\) 例题
因为取值范围是 \([0, m]\),而有 \(m\) 列,则设 \(dp_{i, j}\) 为第 \(i\) 行没有出现 \(j\) 的方案数,则转移易知为 \(dp_{i, j} = \sum\limits_{k = 0}^{j + 1} dp_{i - 1, k} = dp_{i, j - 1} + dp_{i - 1, j + 1}\)。
把它的转移路径画出来(偷个图):
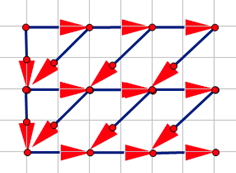
可以转化为(再偷个图):
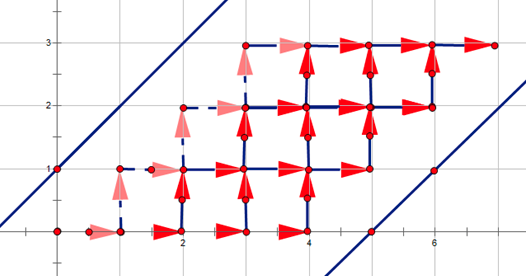
则我们就将其转化成了只能向右或向上走,从 \((0, 0)\) 走到 \((n + m + 1, n)\) 且不经过直线 \(y = x + 1\) 和 \(y = x - m - 2\) 的方案数,直接套用上文的反射容斥即可。
代码。
\(\text{Part 4.}\)习题
Tips:\((x, y)\) 关于 \(y = x + b\) 对称的结果是 \((y - b, x + b)\)。

 反射容斥
反射容斥

 浙公网安备 33010602011771号
浙公网安备 33010602011771号