【算法训练】LeetCode#124 二叉树中的最大路径和

一、描述

124. 二叉树中的最大路径和

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

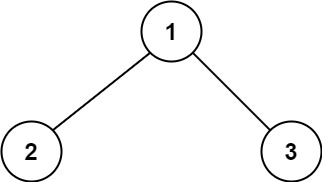
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2:

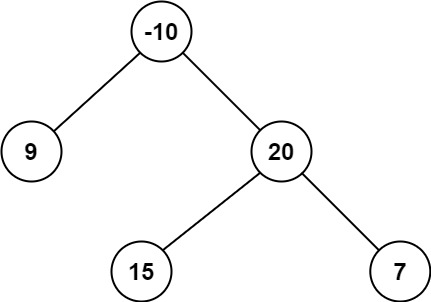
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

二、思路

没思路。。甚至讨论也没思路，直接看了题解，纯纯无语了。

哦，看完题解发现这道题与距节点最远距离很像

其实对于任意节点来说，其能构成的最大路径和一定是左侧子树的最大和加上右侧子树的最大和，并且和大于0才会被采纳。因此对于任意节点都可以向上传递一个：自己能够构成多大路径的信息info，父节点通过info判断是否采纳。

三、解题

public class LeetCode124 {

    public static int result = Integer.MIN_VALUE;

    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {}
        TreeNode(int val) { this.val = val; }
        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }
    public static class Solution {
        public int maxPathSum(TreeNode root) {
            info(root);
            return result;
        }
    }

    public static int info(TreeNode node){
        if (node == null){
            return 0;
        }
        int leftMaxVal = Math.max(info(node.left),0); // 左子树的最大路径和
        int rightMaxVal = Math.max(info(node.right),0); // 右子树的最大路径和

        // 左 + 根 + 右 此时与max判断是否更新
        int curVal = leftMaxVal + rightMaxVal + node.val;
        result = Math.max(result,curVal);

        // 然后再选择子树中最大的路径加上根节点返回上层
        return node.val + Math.max(leftMaxVal,rightMaxVal);
    }
}