Atcoder ABC398.F - ABCBA 题解 KMP的next函数

赛后发现代码有问题，举例：ABCCBAABC

修改后的代码：https://atcoder.jp/contests/abc398/submissions/64144922

---

题目链接：https://atcoder.jp/contests/abc398/tasks/abc398_f

题目大意：

给你一个字符串 \(s\)，要求在字符串 \(s\) 的末尾添加尽可能少的字符使其变成一个回文串。

解题思路：

首先，设输入的字符串为 \(s = s_1 s_2 \ldots s_n\)，设字符串 \(s\) 翻转后的字符串为 \(s'\)。

然后构造一个字符串 \(t = s' + s\)。

比如：

• 若 \(s =\) ABC，则 \(s' =\) CBA，\(t =\) CBAABC
• 若 \(s =\) ABCA，则 \(s' =\) ACBA，\(t =\) ACBAABCA

设字符串 \(s\) 长度为 \(n\)，则字符串 \(t\) 长度为 \(2n\)，对字符串 \(t\) 求 next 数组。

令 \(m = nxt_{2n}\)，则可以发现 \(m\)表示的就是字符串 \(t\) 的最长公共前后缀。

然后可以发现：

如果字符串 \(s\) 本身就是一个回文串，则 \(m \ge n\)，输出 \(s\) 即可。

举例如下：

若 \(m \lt n\)，则 \(m\) 表示的就是字符串的一个最长的是回文串的后缀。

举例如下：

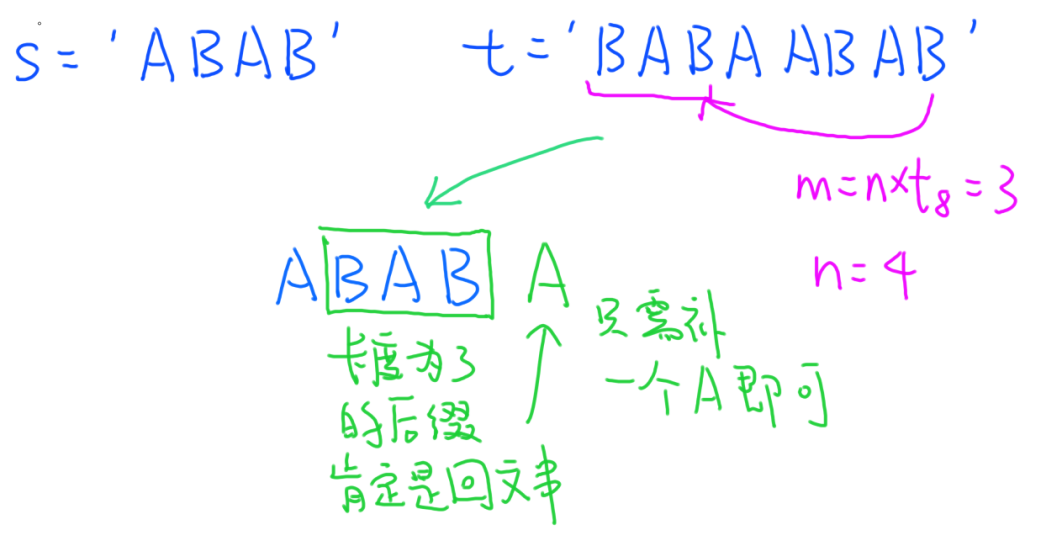
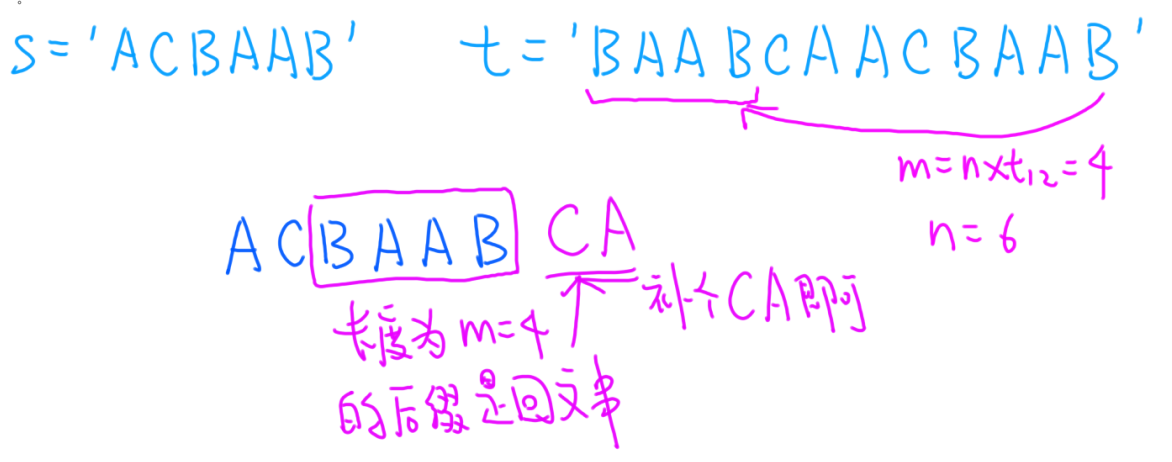
这也就是说，当我们得到 \(m\) 后，我们只需在字符串 \(s\) 的末尾再补充 \(n-m\) 个字符就能构造最短的回文串了。

示例程序：

https://atcoder.jp/contests/abc398/submissions/64068365

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e6 + 5;

char s1[maxn], s[maxn];
int n, nxt[maxn];

int main() {
    scanf("%s", s1+1);
    n = strlen(s1+1);
    strcpy(s+1, s1+1);
    strcpy(s+n+1, s1+1);
    reverse(s+1, s+n+1);
//    cout << s + 1 << endl;

    for (int i = 2, j = 0; i <= 2*n; i++) {
        while (j && s[j+1] != s[i])
            j = nxt[j];
        if (s[j+1] == s[i]) j++;
        nxt[i] = j;
    }
    int m = nxt[2*n];
    if (m >= n)
        puts(s1+1);
    else {
        printf("%s", s1+1);
        for (int i = n-m; i >= 1; i--)
            putchar(s1[i]);
    }

    return 0;
}