随笔分类 - 概率论
摘要：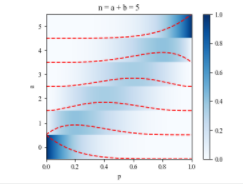
$\Gamma$函数 $\Gamma$函数（Gamma函数）是阶乘函数在实数和复数域的扩展。对于正整数$n$，阶乘函数表示为$n! = 1 \times 2 \times ... \times n$。然而，这个定义仅适用于正整数。Gamma函数的目的是将阶乘扩展到实数和复数域，从而计算实数和复数的“
阅读全文
$\Gamma$函数 $\Gamma$函数（Gamma函数）是阶乘函数在实数和复数域的扩展。对于正整数$n$，阶乘函数表示为$n! = 1 \times 2 \times ... \times n$。然而，这个定义仅适用于正整数。Gamma函数的目的是将阶乘扩展到实数和复数域，从而计算实数和复数的“
阅读全文
摘要：变分自动编码器的大致概念已经理解了快一年多了，但是其中的数学原理还是没有搞懂，在看到相关的变体时，总会被数学公式卡住。下决心搞懂后，在此记录下我的理解。 公式推导——变分下界 这篇文章提出一种拟合数据集分布的方法，拟合分布最常见的应用就是生成模型。该方法遵循极大似然策略，即对于数据集$X = \{x
阅读全文
摘要：在深度学习中，我们通常对模型进行抽样并计算与真实样本之间的损失，来估计模型分布与真实分布之间的差异。并且损失可以定义得很简单，比如二范数即可。但是对于已知参数的两个确定分布之间的差异，我们就要通过推导的方式来计算了。 下面对已知均值与协方差矩阵的两个多维高斯分布之间的KL散度进行推导。当然，因为便于
阅读全文
摘要：以二维正态分布来举例。当方差不变，而协方差变化时，分布沿着长宽比等于两个方差之比的矩阵逐渐变窄。如下图所示： 两个分布的标准差都为0.1，均值都为0，协方差左边从0一直上升到0.01，右边从0下降到-0.01。 看了这个图，有人可能会问，随着协方差的变化，同一高度的椭圆等高线是否始终与矩形相切。看起
阅读全文
摘要：定义 协方差矩阵是用来衡量一组随机变量之间的线性关系的矩阵。我们都知道，对于$n$个随机变量$X_1,X_2,...,X_n$，总体协方差矩阵定义为： $ \left[ \begin{matrix} D(X_1)&Cov(X_1,X_2)&\dots&Cov(X_1,X_n)\\ Cov(X_2,X
阅读全文
摘要：隐马尔可夫模型（Hidden Markov Model, HMM）是可用于标注问题的模型，描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。马尔可夫链不懂的可以把本科的《概率论与数理统计》找回来看一下，并不难，就是离散状态之间的转换。下面直接定义基本概念，为后面的算法做准备。 基本概念 变
阅读全文
摘要：马尔可夫不等式 结论 对于任意非负随机变量$X$，$\forall \epsilon>0$，有： $\displaystyle P(X\ge\epsilon)\le\frac{E(X)}{\epsilon}$ 切比雪夫不等式是它的特例。 证明 $ \begin{align*} E(X) &= \in
阅读全文
摘要：高数 梯度与法向量的关系 求曲面$f(x^{(1)},...,x^{(n)})=0$在$(x^{(1)}_0,...,x^{(n)}_0)$处的法向量（有$f(x^{(1)}_0,...,x^{(n)}_0)=0$），实际上就是求$z = f(x^{(1)},...,x^{(n)})$在$(x^{(
阅读全文
摘要：当我们想对某些特定的分布进行抽样时，由于电脑算法只能产生服从于均匀分布的伪随机数，我们可以通过映射的方式来获取特定分布的抽样。于是引出下面的问题： 假设随机变量$X\sim U(0,1)$，对于已知映射$Y = g(X)$，我们知道如何计算$Y$的概率密度函数。但是，如果我们已知的是$Y$的概率密度
阅读全文
摘要：核密度估计，或称Parzen窗，目标是利用离散的数据本身拟合出一个连续的分布，属于非参数估计。所谓非参数估计，即该估计并没有预设某种分布函数来对其参数进行求解或拟合，比如机器学习中K近邻法也是非参估计的一种。 直方图 首先从直方图切入。对于随机变量$X$的一组抽样，即使$X$的值是连续的，我们也可以
阅读全文
摘要：大数定律 表示试验次数无穷大时，样本均值就等于总体均值。 弱大数定律（辛钦大数定律） $X_1,X_2,X_3,...$是相互独立，服从期望$E(X_k) = \mu$分布的随机变量，则对于任意$\epsilon>0$，有： $\displaystyle \lim_{n\to \infty}P\le
阅读全文
摘要：朴素贝叶斯法，就是使用贝叶斯公式的学习方法，朴素就是它假设输入变量（向量）的各个分量之间是相互独立的。所以对于分量之间不独立的分布，如果使用它学习和预测效果就不会很好。 简化策略 它是目标是通过训练数据集学习联合概率分布$P(X, Y)$用来预测。书上说，具体是先学习到先验概率分布以及条件概率分布，
阅读全文
摘要：样本均值和样本方差的无偏性 对于独立同分布的样本$x_1...x_n$来说，他们的均值为与方差分别为： $ \begin{aligned}&\bar{x} = \frac{1}{n}\sum\limits_{i=1}^{n}x_i \\& s^2 = \frac{\sum\limits_{i=1}^
阅读全文
浙公网安备 33010602011771号