leetcode 4. 两个有序数组的中位数(第k大的数)

假设有前 k 小的数，分配到两个数组中

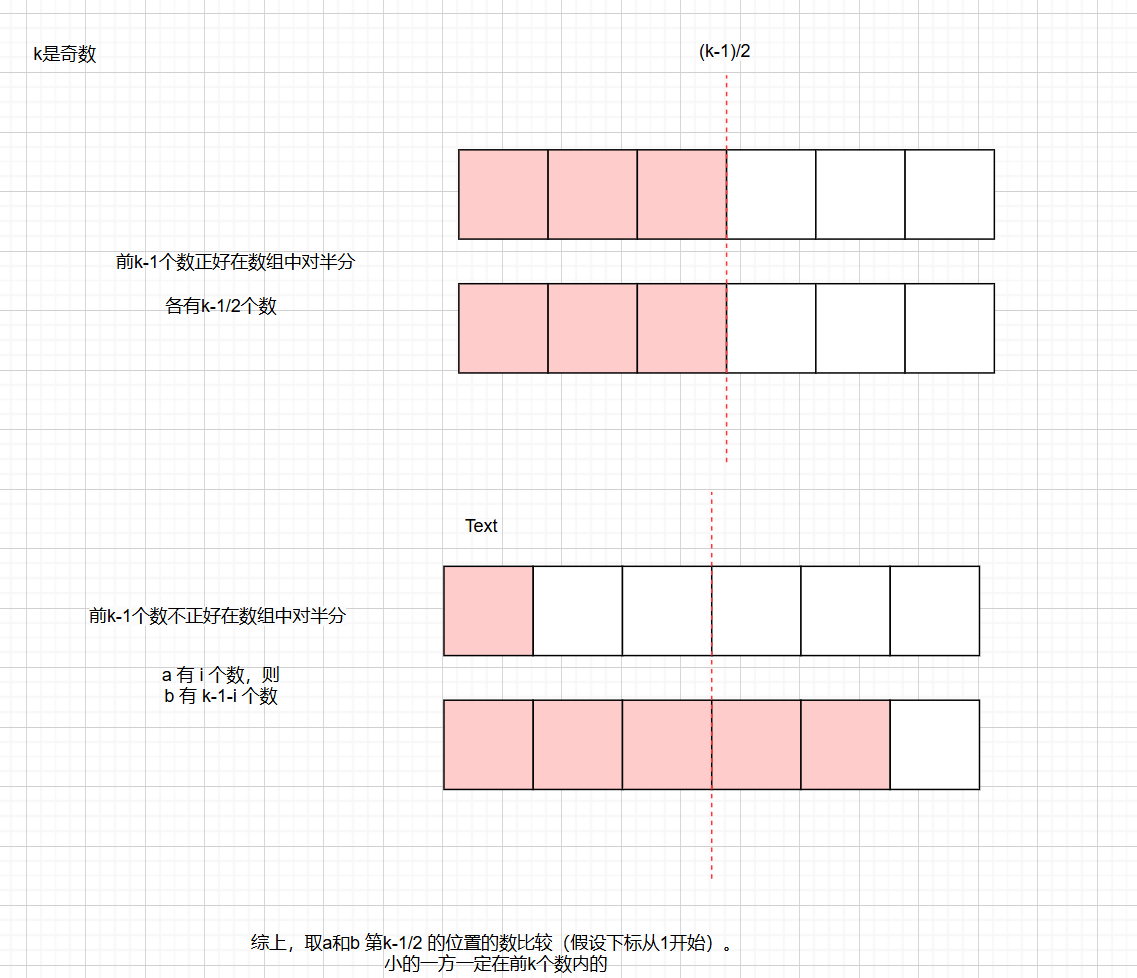
综上，
前k-1数的边界偏离(k-1)/2 时，由于大于(k-1)数边界的挤压会伴随小于k的数的边界的外延，
其在(k-1)/2会呈现一方比另一方大的情况，可以直接判定小的一方在小于k的数的边界内
而当k-1数正好在边界内，则同样可以判定小的数在小于k的前k-1数的边界内
这样将前k-1的数排除后，取从剩余两数组中取较小的一个即可
以上是不严谨的直观理解

边界问题

1. 如果 A[k/2−1] 或者 B[k/2−1] 越界，那么我们可以选取对应数组中的最后一个元素。在这种情况下，我们必须根据排除数的个数减少 k 的值，而不能直接将 k 减去 k/2。

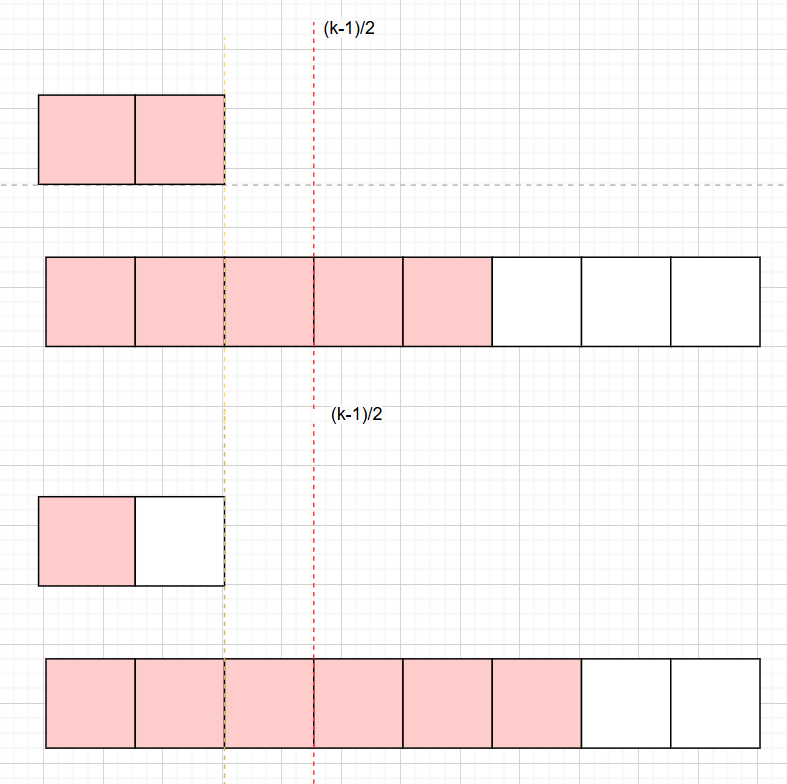
2. 如果一个数组为空，说明该数组中的所有元素都被排除，我们可以直接返回另一个数组中第 k 小的元素。

3. 如果 k=1，我们只要返回两个数组首元素的最小值即可。

证明与代码实现

转自 https://blog.csdn.net/yutianzuijin/article/details/11499917

首先假设数组A和B的元素个数都大于k/2，我们比较A[k/2-1]和B[k/2-1]两个元素，这两个元素分别表示A的第k/2小的元素和B的第k/2小的元素。这两个元素比较共有三种情况：>、<和=。如果A[k/2-1]<B[k/2-1]，这表示A[0]到A[k/2-1]的元素都在A和B合并之后的前k小的元素中。换句话说，A[k/2-1]不可能大于两数组合并之后的第k小值，所以我们可以将其抛弃。

证明也很简单，可以采用反证法。假设A[k/2-1]大于合并之后的第k小值，我们不妨假定其为第（k+1）小值。由于A[k/2-1]小于B[k/2-1]，所以B[k/2-1]至少是第（k+2）小值。但实际上，在A中至多存在k/2-1个元素小于A[k/2-1]，B中也至多存在k/2-1个元素小于A[k/2-1]，所以小于A[k/2-1]的元素个数至多有k/2+ k/2-2，小于k，这与A[k/2-1]是第（k+1）的数矛盾。

当A[k/2-1]>B[k/2-1]时存在类似的结论。

当A[k/2-1]=B[k/2-1]时，我们已经找到了第k小的数，也即这个相等的元素，我们将其记为m。由于在A和B中分别有k/2-1个元素小于m，所以m即是第k小的数。(这里可能有人会有疑问，如果k为奇数，则m不是中位数。这里是进行了理想化考虑，在实际代码中略有不同，是先求k/2，然后利用k-k/2获得另一个数。)

通过上面的分析，我们即可以采用递归的方式实现寻找第k小的数。此外我们还需要考虑几个边界条件：

如果A或者B为空，则直接返回B[k-1]或者A[k-1]；
如果k为1，我们只需要返回A[0]和B[0]中的较小值；
如果A[k/2-1]=B[k/2-1]，返回其中一个；
最终实现的代码为：

int min(int a,int b){
    return a<b?a,b;
}

double findKth(int a[], int m, int b[], int n, int k)
{
	//always assume that m is equal or smaller than n
	if (m > n)
		return findKth(b, n, a, m, k);
	if (m == 0)
		return b[k - 1];
	if (k == 1)
		return min(a[0],b[0]);
	// 注意 k/2 越界情况，由于 n>m，所以只有pa指向m尾一种情况
	int pa = min(k/2,m), pb = k - pa;
	if (a[pa - 1] < b[pb - 1])
		return findKth(a + pa, m - pa, b, n, k - pa);
	else if (a[pa - 1] > b[pb - 1])
		return findKth(a, m, b + pb, n - pb, k - pb);
	else
		return a[pa - 1];
}

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int * A = nums1,*B = nums2;
    int m = nums1Size,n=nums2Size;
    int total = m + n;
    if (total & 0x1)
        return findKth(A, m, B, n, total / 2 + 1);
    else
        return (findKth(A, m, B, n, total / 2)
                + findKth(A, m, B, n, total / 2 + 1)) / 2;
}