P1873 [COCI 2011/2012 #5] EKO / 砍树

题目描述

伐木工人 Mirko 需要砍 $M$ 米长的木材。对 Mirko 来说这是很简单的工作，因为他有一个漂亮的新伐木机，可以如野火一般砍伐森林。不过，Mirko 只被允许砍伐一排树。

Mirko 的伐木机工作流程如下：Mirko 设置一个高度参数 $H$（米），伐木机升起一个巨大的锯片到高度 $H$，并锯掉所有树比 $H$ 高的部分（当然，树木不高于 $H$ 米的部分保持不变）。Mirko 就得到树木被锯下的部分。例如，如果一排树的高度分别为 $20,15,10$ 和 $17$，Mirko 把锯片升到 $15$ 米的高度，切割后树木剩下的高度将是 $15,15,10$ 和 $15$，而 Mirko 将从第 $1$ 棵树得到 $5$ 米，从第 $4$ 棵树得到 $2$ 米，共得到 $7$ 米木材。

Mirko 非常关注生态保护，所以他不会砍掉过多的木材。这也是他尽可能高地设定伐木机锯片的原因。请帮助 Mirko 找到伐木机锯片的最大的整数高度 $H$，使得他能得到的木材至少为 $M$ 米。换句话说，如果再升高 $1$ 米，他将得不到 $M$ 米木材。

输入格式

第 $1$ 行 $2$ 个整数 $N$ 和 $M$，$N$ 表示树木的数量，$M$ 表示需要的木材总长度。

第 $2$ 行 $N$ 个整数表示每棵树的高度。

输出格式

$1$ 个整数，表示锯片的最高高度。

输入输出样例 #1

输入 #1

4 7
20 15 10 17

输出 #1

15

输入输出样例 #2

输入 #2

5 20
4 42 40 26 46

输出 #2

36

说明/提示

对于 $100%$ 的测试数据，$1\le N\le10^6$，$1\le M\le2\times10^9$，树的高度 $\le 4\times 10^5$，所有树的高度总和 $>M$。

---

思路 超时

单纯的从高到低排后，从最高的h开始尝试

#include <bits/stdc++.h>
using namespace std;

/*
    砍树
*/
int n,m;
int a[2000001];
int main(){
    cin >> n >> m;
    for(int i=0;i<n;i++){
        scanf("%d",a+i);
    }
    // 排序后从大头开始尝试
    sort(a,a+n,[](int a,int b){
        return a>b;
    });
    int sum=0;
    // sum大于 所需m 时停止
    int h=a[0]-1;
    while(sum<m){
        for(int i =0;i<n&&a[i]>h;i++){
            sum+=a[i]-h;
        }
        if(sum<m){
            sum=0;
            h--;
        }
    }
    cout << h;
}

优化

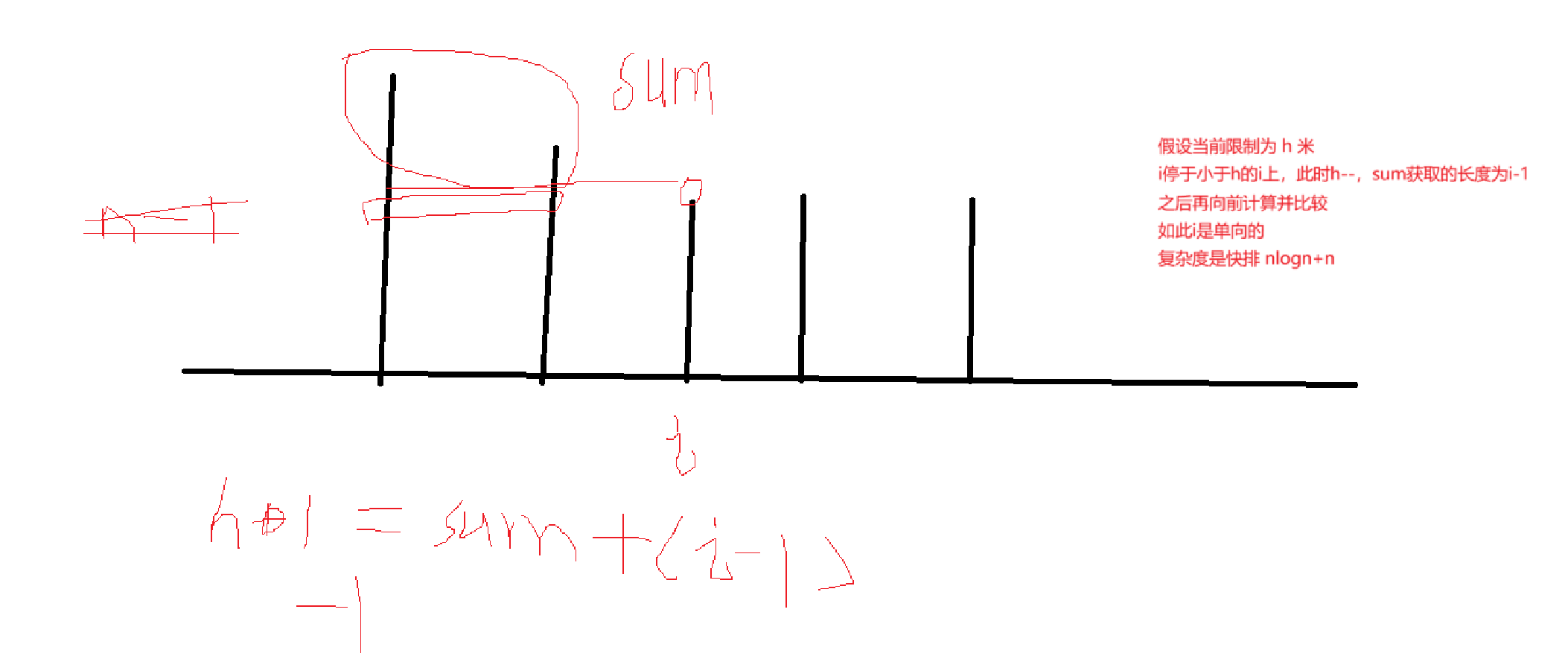
优化了i的回溯，利用数组的单调性

限制为h以上时，sum不够，此时i前的被砍的高度都为h
则h--后，sum获取的高度为 i(i从0开始)，之后i再先前计算，避免了回溯

#include <bits/stdc++.h>
using namespace std;

/*
    砍树
*/
int n,m;
int a[2000001];
int main(){
    cin >> n >> m;
    for(int i=0;i<n;i++){
        scanf("%d",a+i);
    }
    // 排序后从大头开始尝试
    sort(a,a+n,[](int a,int b){
        return a>b;
    });
    int sum=0;
    // sum大于 所需m 时停止
    int h=a[0]-1;
    int i=0;
    while(sum<m){
        for(;i<n&&a[i]>h;i++){
            sum+=a[i]-h;
        }
        if(sum<m){
            h--;
            sum+=i; // 不回溯，h--后直接知道砍过的树的新获取木材量
        }
    }
    cout << h;
}