P2241 统计方形（数据加强版）

题目背景

1997年普及组第一题

题目描述

有一个 $n \times m$ 方格的棋盘，求其方格包含多少正方形、长方形（不包含正方形）。

输入格式

一行，两个正整数 $n,m$（$n \leq 5000,m \leq 5000$）。

输出格式

一行，两个正整数，分别表示方格包含多少正方形、长方形（不包含正方形）。

输入输出样例 #1

输入 #1

2 3

输出 #1

8 10

---

首先是矩形的个数,可以用选择两条横线与两条竖线相交的排列组合得出 因为可以得到矩形的总个数为

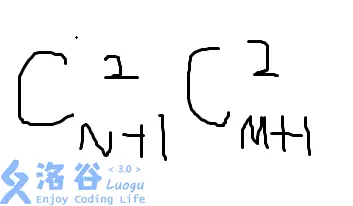
正方形边长一定 <= Min(m,n);

设边长是 a（<= Min(m,n)）， 则x坐标有（n-a+1）
可能y坐标有（m-a+1）
对于边长a正方形有 （m-a+1)(n-a+1）个
总共有 Min(m,n)* （m-a+1)(n-a+1）个

和 i=0 n=Min(m,n) （m-a+1)(n-a+1）

2+1 * 2

#include <bits/stdc++.h>
using namespace std;

int main() {
    int m, n;
    cin >> m >> n;

    // 计算正方形数量
    long long sq = 0;
    for (int i = 1; i <= min(m, n); i++) {
        sq += (m - i + 1) * (n - i + 1);
    }

    // 计算矩形数量
    long long rect = (long long)(m + 1) * m / 2 * (n + 1) * n / 2;

    rect -= sq;

    // 输出结果
    cout << sq << " " << rect;

    return 0;
}