PCL_3: K-D Tree、OCTrees
介绍
K-D Tree 和 OCTrees 原理和方法。
K-D Tree
通过3D相机(雷达、激光扫描、立体相机)获取到的点云,一般数据量较大,分布不均匀,数据主要表征了目标物表面的大量点的集合,这些离散的点如果希望实现基于邻域关系的快速查找比对功能,就必须对这些离散的点之间建立拓扑关系。常见的空间索引一般是自上而下逐级划分空间的各种索引结构,包括BSP树,k-d tree、KDB tree、R tree、CELL tree、八叉树等。有了这些关系,我们就可以实现点云的降采样,计算特征向量,点云匹配,点云拆分等功能。
原理
k-d tree( k-dimensional tree)是计算机科学中用于在k维空间中一些点建立关系的数据结构。它是一个包含特定约束的二叉搜索树。k-d tree对于范围搜索和最近邻居搜索非常有用。我们通常只处理三维空间的点云,因此我们所有的k-d树都是三维空间的。
k-d树的每个级别都使用垂直于相应轴的超平面沿特定维度拆分所有子级。在树的根部,所有子项都将根据第一维进行拆分(即,如果第一维坐标小于根,则它将位于左子树中,如果大于根,则显然位于右边的子树)。树中向下的每个级别都在下一个维度上划分,其他所有元素都用尽后,将返回到第一个维度。他们构建k-d树的最有效方法是使用一种分区方法,例如快速排序所用的一种方法,将中值点放置在根上,所有具有较小一维值的东西都放置在根部,而右侧则更大。然后,在左右两个子树上都重复此过程,直到要分区的最后一棵树仅由一个元素组成。
具体可以看https://robot.czxy.com/docs/pcl/chapter01/decomposition/
代码示例
以下案例通过两种方式进行邻域搜索
方式一:指定搜索最近的K个邻居
方式二:通过指定半径搜索邻居
#include <pcl/point_cloud.h>
#include <pcl/kdtree/kdtree_flann.h>
#include <iostream>
#include <vector>
#include <ctime>
//#include <pcl/search/kdtree.h>
//#include <pcl/search/impl/search.hpp>
#include <pcl/visualization/cloud_viewer.h>
int main(int argc, char **argv) {
// 用系统时间初始化随机种子
srand(time(NULL));
// 创建点云数据
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
// 生成点云数据1000个
cloud->width = 1000;
cloud->height = 1; // 1 表示点云为无序点云
cloud->points.resize(cloud->width * cloud->height);
// 给点云填充数据 0 - 1023
for (size_t i = 0; i < cloud->points.size(); ++i) {
cloud->points[i].x = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud->points[i].y = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud->points[i].z = 1024.0f * rand() / (RAND_MAX + 1.0f);
}
// 创建KdTree的实现类KdTreeFLANN (Fast Library for Approximate Nearest Neighbor)
pcl::KdTreeFLANN<pcl::PointXYZ> kdtree;
// pcl::search::KdTree<pcl::PointXYZ> kdtree; // 这个也可以
// 设置搜索空间,把cloud作为输入
kdtree.setInputCloud(cloud);
// 初始化一个随机的点,作为查询点
pcl::PointXYZ searchPoint;
searchPoint.x = 1024.0f * rand() / (RAND_MAX + 1.0f);
searchPoint.y = 1024.0f * rand() / (RAND_MAX + 1.0f);
searchPoint.z = 1024.0f * rand() / (RAND_MAX + 1.0f);
// K nearest neighbor search
// 方式一:搜索K个最近邻居
// 创建K和两个向量来保存搜索到的数据
// K = 10 表示搜索10个临近点
// pointIdxNKNSearch 保存搜索到的临近点的索引
// pointNKNSquaredDistance 保存对应临近点的距离的平方
int K = 10;
std::vector<int> pointIdxNKNSearch(K); // 保存搜索到的临近点的索引
std::vector<float> pointNKNSquaredDistance(K); // 保存对应临近点的距离的平方
// 当前点的位置
std::cout << "K nearest neighbor search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with K=" << K << std::endl;
// 搜索K个临近点
if (kdtree.nearestKSearch(searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance) > 0) {
for (size_t i = 0; i < pointIdxNKNSearch.size(); ++i)
std::cout << " " << cloud->points[pointIdxNKNSearch[i]].x
<< " " << cloud->points[pointIdxNKNSearch[i]].y
<< " " << cloud->points[pointIdxNKNSearch[i]].z
<< " (距离平方: " << pointNKNSquaredDistance[i] << ")" << std::endl;
}
// Neighbors within radius search
// 方式二:通过指定半径搜索
std::vector<int> pointIdxRadiusSearch;
std::vector<float> pointRadiusSquaredDistance;
// 创建一个随机[0,256)的半径值
float radius = 256.0f * rand() / (RAND_MAX + 1.0f);
std::cout << "Neighbors within radius search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with radius=" << radius << std::endl;
// 搜索半径内的临近点
if (kdtree.radiusSearch(searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0) {
for (size_t i = 0; i < pointIdxRadiusSearch.size(); ++i)
std::cout << " " << cloud->points[pointIdxRadiusSearch[i]].x
<< " " << cloud->points[pointIdxRadiusSearch[i]].y
<< " " << cloud->points[pointIdxRadiusSearch[i]].z
<< " (距离平方:: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
}
// 可视化
pcl::visualization::PCLVisualizer viewer("PCL Viewer");
viewer.setBackgroundColor(0.0, 0.0, 0.5); // 设置背景颜色
viewer.addPointCloud<pcl::PointXYZ>(cloud, "cloud"); // 添加点云数据
pcl::PointXYZ originPoint(0.0, 0.0, 0.0); // 创建一个原点
// 添加从原点到搜索点的线段
viewer.addLine(originPoint, searchPoint); // 添加线段
// 添加一个以搜索点为圆心,搜索半径为半径的球体
viewer.addSphere(searchPoint, radius, "sphere", 0); // 添加球体
// 添加一个放到200倍后的坐标系
viewer.addCoordinateSystem(200); // 添加坐标系
// 循环显示
while (!viewer.wasStopped()) {
viewer.spinOnce();
}
return 0;
}
效果
octree八叉树
建立空间索引在点云数据处理中已被广泛应用,常见空间索引一般是自顶向下逐级划分空间的各种空间索引结构,比较有代表性的包括 BSP 树、KD 树、KDB 树、 R树、R+树、CELL 树、四叉树和八叉树等索引结构,而在这些结构中 KD 树和八叉树在 3D点云数据排列中应用较为广泛。 PCL 对八叉树的数据结构建立和索引方法进行了实现,以方便在此基础上对点云进行处理操作 。
原理
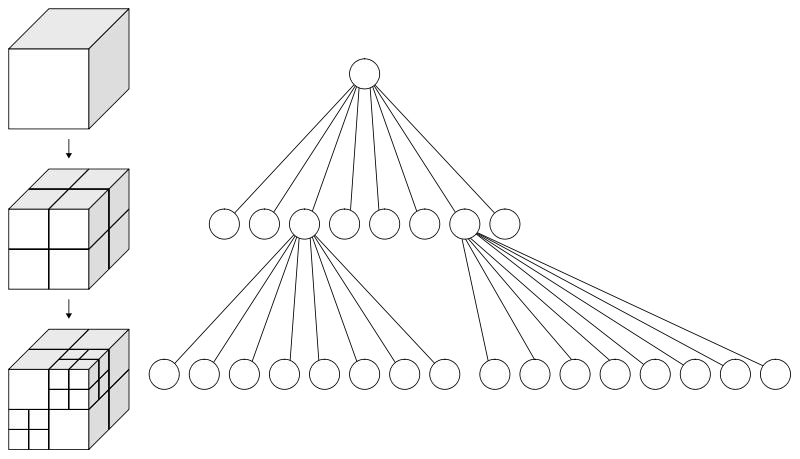

这里引入了一个概念:Voxel翻译为体积元素,简称体素。描述了一个预设的最小单位的正方体
pcl的octree库提供了从点云数据创建具有层次的数据结构的方法。这样就可以对点数据集进行空间分区,下采样和搜索操作。每个八叉树节点有八个子节点或没有子节点。根节点描述了一个包围所有点的3维包容盒子。
pcl_octree实现提供了有效的最近邻居搜索(邻域搜索)API,例如“ 体素(Voxel)邻居搜索”,“ K最近邻居搜索”和“半径搜索邻居”。叶子节点类也提供其他功能,例如空间“占用率”和“每个体素(Voxel)的点密度”检查;序列化和反序列化功能可将八叉树结构有效地编码为二进制格式;此外,内存池实现减少了昂贵的内存分配和释放操作,以便快速创建八叉树。
下图说明了最低树级别的八叉树节点的体素边界框。八叉树体素围绕着兔子表面的每个3D点。红点代表点数据。该图像是使用octree_viewer创建的.

代码
#include <pcl/point_cloud.h>
#include <pcl/octree/octree_search.h>
#include <iostream>
#include <vector>
#include <ctime>
#include <pcl/visualization/cloud_viewer.h>
int
main(int argc, char **argv) {
srand((unsigned int) time(NULL));
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
// Generate pointcloud data
cloud->width = 1000;
cloud->height = 1;
cloud->points.resize(cloud->width * cloud->height);
for (size_t i = 0; i < cloud->points.size(); ++i) {
cloud->points[i].x = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud->points[i].y = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud->points[i].z = 1024.0f * rand() / (RAND_MAX + 1.0f);
}
// float resolution = 0.01f;
// 设置分辨率为128
float resolution = 128.0f;
// resolution该参数描述了octree叶子leaf节点的最小体素尺寸。
pcl::octree::OctreePointCloudSearch<pcl::PointXYZ> octree(resolution);
// 设置输入点云
octree.setInputCloud(cloud);
// 通过点云构建octree
octree.addPointsFromInputCloud();
pcl::PointXYZ searchPoint;
searchPoint.x = 1024.0f * rand() / (RAND_MAX + 1.0f);
searchPoint.y = 1024.0f * rand() / (RAND_MAX + 1.0f);
searchPoint.z = 1024.0f * rand() / (RAND_MAX + 1.0f);
// Neighbors within voxel search
// 方式一:“体素近邻搜索”,它把查询点所在的体素中其他点的索引作为查询结果返回,
// 结果以点索引向量的形式保存,因此搜索点和搜索结果之间的距离取决于八叉树的分辨率参数
std::vector<int> pointIdxVec;
if (octree.voxelSearch(searchPoint, pointIdxVec)) {
std::cout << "Neighbors within voxel search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z << ")"
<< std::endl;
for (size_t i = 0; i < pointIdxVec.size(); ++i)
std::cout << " " << cloud->points[pointIdxVec[i]].x
<< " " << cloud->points[pointIdxVec[i]].y
<< " " << cloud->points[pointIdxVec[i]].z << std::endl;
}
// K nearest neighbor search
// 方式二:K 近邻搜索,本例中K被设置成10, "K 近邻搜索”方法把搜索结果写到两个分开的向量中,
// 第一个pointIdxNKNSearch 包含搜索结果〈结果点的索引的向量〉
// 第二个pointNKNSquaredDistance 保存相应的搜索点和近邻之间的距离平方。
int K = 10;
std::vector<int> pointIdxNKNSearch;
std::vector<float> pointNKNSquaredDistance;
std::cout << "K nearest neighbor search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with K=" << K << std::endl;
if (octree.nearestKSearch(searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance) > 0) {
for (size_t i = 0; i < pointIdxNKNSearch.size(); ++i)
std::cout << " " << cloud->points[pointIdxNKNSearch[i]].x
<< " " << cloud->points[pointIdxNKNSearch[i]].y
<< " " << cloud->points[pointIdxNKNSearch[i]].z
<< " (squared distance: " << pointNKNSquaredDistance[i] << ")" << std::endl;
}
// Neighbors within radius search
// 方式三:半径内近邻搜索
// “半径内近邻搜索”原理和“K 近邻搜索”类似,它的搜索结果被写入两个分开的向量中,
// 这两个向量分别存储结果点的索引和对应的距离平方
std::vector<int> pointIdxRadiusSearch;
std::vector<float> pointRadiusSquaredDistance;
float radius = 256.0f * rand() / (RAND_MAX + 1.0f);
std::cout << "Neighbors within radius search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with radius=" << radius << std::endl;
if (octree.radiusSearch(searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0) {
for (size_t i = 0; i < pointIdxRadiusSearch.size(); ++i)
std::cout << " " << cloud->points[pointIdxRadiusSearch[i]].x
<< " " << cloud->points[pointIdxRadiusSearch[i]].y
<< " " << cloud->points[pointIdxRadiusSearch[i]].z
<< " (squared distance: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
}
pcl::visualization::PCLVisualizer viewer("PCL Viewer");
viewer.setBackgroundColor(0.0, 0.0, 0.5);
viewer.addPointCloud<pcl::PointXYZ>(cloud, "cloud");
pcl::PointXYZ originPoint(0.0, 0.0, 0.0);
// 添加从原点到搜索点的线段
viewer.addLine(originPoint, searchPoint);
// 添加一个以搜索点为圆心,搜索半径为半径的球体
viewer.addSphere(searchPoint, radius, "sphere", 0);
// 添加一个放到200倍后的坐标系
viewer.addCoordinateSystem(200);
while (!viewer.wasStopped()) {
viewer.spinOnce();
}
}
cmake
# 1. 必要的设置
cmake_minimum_required(VERSION 3.15) # 最低版本号
project(test) # 项目名称
set(CMAKE_CXX_STANDARD 17) # C++17
set(EXEC_NAME exec) # 可执行文件名称
# set(EXECUTABLE_OUTPUT_PATH ${PROJECT_SOURCE_DIR}/build/bin) # 1可执行文件输出路径
# set(RUNTIME_OUTPUT_DIRECTORY ${PROJECT_SOURCE_DIR}/build/bin) # 2可执行文件输出路径
# set(RUNTIME_OUTPUT_DIRECTORY_DEBUG ${PROJECT_SOURCE_DIR}/build/bin/debug)
# set(RUNTIME_OUTPUT_DIRECTORY_RELEASE ${PROJECT_SOURCE_DIR}/build/bin/release)
# 2. 代码文件检索
file(GLOB SRC_list ${PROJECT_SOURCE_DIR}/src/*.cpp) # 查找src下的所有cpp文件
# file(GLOB_RECURES SRC_list ${PROJECT_SOURCE_DIR}/src/*.cpp)
# 3. ------------------------- PCL -------------------------
find_package(PCL 1.2 REQUIRED)
include_directories(${PCL_INCLUDE_DIRS})
link_directories(${PCL_LIBRARY_DIRS})
add_definitions(${PCL_DEFINITIONS})
# 4. 添加可执行文件
add_executable(${EXEC_NAME} ${SRC_list})
# 5. 连接
target_link_libraries(${EXEC_NAME} ${PCL_LIBRARIES})
# cmake .. -G "MinGW Makefiles"
# cmake -G "Visual Studio 17 2022" -A x64 ..
# cmake -G "Visual Studio 16 2019" -A x64 ..
# cmake -G "Ninja" ..
# cmake -G "Unix Makefiles" ..
# cmake --build . --config Release




 浙公网安备 33010602011771号
浙公网安备 33010602011771号