讲课记录
Update on 7.18 好像初步完工了!!!
写的很简单,后面在完善。
发现写的越来越水了!!!
D1 dp (lyc)
凸性:ppt
边际效应:对应着决策单调性,两个东西,同时加上一个东西,多的东西加的多。
二维的边际效应:四边形不等式,就是两条一长一短的线段,同时加一个东西,给长区间加一个东西,比给短区间加一个东西代价更大。
四边形不等式能推出决策单调性和完全单调性
2D/1D: 形如 \(f_{k,i} + \omega(j,i) \to f_{k+1,j}\),假设 \(\omega(j,i)\) 满足决策单调性。我们有一个分治做法,能做到 \(O(n k \log n)\),对于一个区间 \(\left[l,r\right]\),我们找到中点 \(mid\),暴力计算,接着直接分治,只不过有决策单调性,可以不用遍历完。
课上讲的是 CF1603D。
完全单调性:对于任意 $ 𝑖<𝑗 $,在一个前缀中从 \(𝑖\) 转移更好,在一个后缀中从 \(𝑗\) 转移更好。
二分队列:
状态设计技巧:在最优化问题中,一个常用的方法是:
先设计一个取值为 0/1 的状态,然后利用单调性去掉一维。
举例子:CF1870E
如果某个转移区间能被其他东西替代,那么不优。
也可做上面那道题。
还有一个 CF1768F。
WQS二分:
dp 设计原理:感觉是状态设计。
课上的例题好像忘了( 这个
但是实际上是这样的:我们写考虑判定,再将判定的变量加入 dp。
例题:UOJ748,有点抽象啊
dp of dp:判定换为 dp,一般状态不会多。
一些奇怪的状态:Gym103466I(状压的东西不太正常)
ABC225F(邻项交换法,倒序),CF1810G(和前面差不多,wzy 讲的)
这里是题解
CF1603D
每一步都很自然的 *3000。
根据上课讲的东西,决策单调性显然,注意到 \(\log_2(k) \geq n\) 时直接能构造出为 \(n\) 的解,然后套用分治即可。还需要一些数论技巧。
CF833B P5574 CF868F
根据上课讲的东西,决策单调性显然。算是三倍经验了。
P1912
二分队列。
AT_abc225_f
CF1810G
在dp选讲写了。
P8321
在dp选讲写了。
CF1870E
有意思题目,第一种做法就是设 \(dp_{i,j}\) 表示 第 \(i\) 项的答案是否能为 \(j\),让他成为 0/1 dp。把单调的一维设为状态。所以是 \(dp_{j} = i\)。类似于 dijkstra 转移即可。第二种是转移优化,直接因为本题中,只有极短 mex 区间是有用的。即,若 \(\left[𝑖,𝑗]=[𝑖−1,𝑗 \right]\),或 \(\left[𝑖,𝑗\right]=\left[𝑖,𝑗−1 \right]\),那么这个区间就是无用的。这样的区间只有 \(𝑂(𝑛)\) 个。
证明看看第一篇题解,多头上课没证明出来。(
UOJ748
考虑如何判定这个东西,我们如果能匹配就匹配了,如果不能匹配,我们就直接,让前面的数当做插入的,保证合法就行。
能我们只需要设 \(dp_{v,x,y}\) 表示已经匹配了长度为 \(v\) 的前缀,插入了 \(x\) 个 0,\(y\) 个 1。转移不难。
2019 ICPC Nanjing 区域赛 I(QOJ7063)
先考虑 \(1\le a_{i} \le 50\) 怎么做,我们有一个直观的想法就是对达到的点进行状压。显然不对。但是我们真的需要这样做吗,我们只需要把到达的点的权值进行状压就行了。直接把这个东西的哈希值放在状态里面就行了。对于权值 \(\geq 50\) 的情况,我们是不是直接乘上一个组合数进行了。对于 \(0\) 的情况也是同理。
P10141
有一个 \(O(n^4)\) 的 Dp,设 \(dp_{l,r,x}\) 代表在 \(\left[l,r\right]\) 的这个区间,\(x\) 能留下来的概率,这个不好,我们反着做,设 \(dp_{l,r}\) 代表为 \(\left[ l,r\right]\) 这个区间能留下来的概率,是 \(O(n^3)\) 的,这个题后面的部分没有意义就不写了。
P2224
P3188
CF1768F
GYM102538H
D2 math (lsy)
?
前面是为后面符号做铺垫。直接贺 PPT 吧。
上午讲的直接贺 PPT 了。疑似太形式化了。
前面是一些 Tricky 东西
后面是容斥原理,二项式反演,子集反演。
贺了一个图

DAG容斥:?,容斥系数的推导。
GF:讲的东西有点 Trivial。
这里是题解
P4159
分层图,然后做完了。
P10143
考虑算贡献,分两种情况, 太简单了,没啥好说的。
P7961
经典永流传属实了,直接设 \(dp_{i,j,k,l}\) 表示 目前从低到高确定了第 \(i\) 位,目前确定了 \(j\) 个数,目前 \(1\) 的个数为 \(k\),上一位进位了 \(l\)的所有答案,考虑怎样转移,就是转移到 \(dp_{i+1,j+t,k+(l+t) \bmod 2,l+ \left\lfloor \frac{(l+t)}{2} \right\rfloor }\),现在来确定一下系数,注意到贡献是乘积的形式,所以可以乘上 \({n-j \choose t} v_{i} ^ t\),然后就做完,注意下最后算答案的时候处理一下进位合不合法。
P5664
怎么还是经典题,先考虑容斥,不看最后一条限制,答案是 \(\sum\limits_{i=1}^{n}(1+\prod\limits_{j=1}^{m} a_{i,j}) -1\),有一个经典的观察是最多只有一种主要食材不合法,直接枚举它,我们设 \(dp_{i,j,k}\) 表示前 \(i\)项,不合法的选了 \(j\) 个,合法的选了 \(k\) 个。是 \(O(nm^3)\) 的。注意到当且仅当 \(j-k \geq 0\) 时才能算贡献,直接把后面那一坨换成差值就可以了,是 \(O(nm^2)\),可以通过。
AT_arc154_e
不是题目难度差距巨大啊。
怎么感觉这个题不难
需要一点注意力。
前面 \(i^2\) 项对原来的贡献就是 \({n+1 \choose 2}^m\),乘起来。
后面不好算,考虑期望乘上总方案数, 就是\(E\left[\sum\limits_{i} i{p_i}\right] = \sum\limits_{i} p_i \times E\left[pos_{p_{i}}\right]\)
上面那一步有点牛,因为他是排列。
首先没有换过的概率就是 \((1-\frac{(n-i+1)i}{\frac{n(n+1)}{2}})^m\),期望位置为 \(i\)。
我们考虑一个点 \(i\)。通过一次操作把它挪到点 \(j\) 的方案数显然是 \(\min(i,n−i+1,j,n−j+1)\)
注意到 \(j\) 和 \(n-j+1\) 本质相同,所以我们期望是 \(\frac{n+1}{2}\),是不是很牛。概率从前面的减就可以了。
那我们就做完了。
AT_yahoo_procon2019_qual_e
权值和是奇数就是异或和为 \(1\) ,考虑线性基。
我们假设选出了一些行,异或后的序列为 \(B_1,B_2,\dotsb B_m\)。
我们想知道有多少个子集异或为 \(1\),注意到 \(\forall B_i\),\(B_i \in \left[0,1\right]\)。我们构造出来线性基,显然是 \(1\),对于剩下的 \(m-1\) 个数,对于 \(2^{m-1}\) 可能的情况,都能构造出来他们为 \(1\),所以就是 \(2^{m-1}\),但是对吗?如果我们序列所有数都为 \(0\),那不就炸了吗。考虑容斥,我们把每一列的数凑起来看成一个整体,问题变为了一个序列 \(C_1,C_2,\dotsb C_n\)。我们要选出来有多少个子集异或为 \(0\)。那不就是线性基吗,把所有数加进线性基,答案就是 \(2^{n-线性基大小}\)。还是一样的道理,线性基内可以构造,外面任选。那们一共就有 \(2^n-2^{n-线性基大小}\) 种合法的,再乘上 \(2^{m-1}\) 可能的情况就行了。
总结:线性基是极大线性无关组的性质一般都是题目的突破口。
感觉挺深刻的。
P3265
不就是线性基板子吗,注意到线性基是满足拟阵的。
P4570
从大到小排序,线性基板子。
P3292
我不会告诉你我是树剖+线段树过的
现在看来直接倍增就可以了,对的对的。
AT_abc223_h
不难。
P4151
有趣,老题新做。
我们注意到如果只有一条路径,那们答案直接就是 \(dis_{n}\),不妨考虑的时候借助生成树,分析每条非树边怎么加进去。我们注意到有一个环的情况,就是异或的时候加上环上一圈的异或值,那么所有的情况是同理的。我们把所有环找出来做一遍线性基即可。还有一个问题,我们到 \(n\) 的路径不止一条,但是我们是高贵的线性基,所以就是对的!!!
还是一句话:线性基是极大线性无关组。
版本T0相关
实际不全是。
AT_tokiomarine2020_e
P3349
上面两个都是子集反演。感觉不难。
[CEOI 2019] Amusement Park
经典题*1
我们发现对于一个合法的 DAG,若可以通过原图操作 \(x\) 次得到,我们也可已通过 \(m-x\) 得到一个反向的合法 DAG,那们变成了一个计数 DAG 个数问题,再乘个 \(\frac{m}{2}\) 就是答案。
第一次做大概率做不出来的,这里直接说怎么做。注意到数据范围很小,考虑一下状压,设 \(dp_{S}\) 点集为 \(S\) 时的答案,对于这一类问题,我们有一种通用的想法,我每一次考虑将一个互相独立的点的集合加入转移,如下图所示:
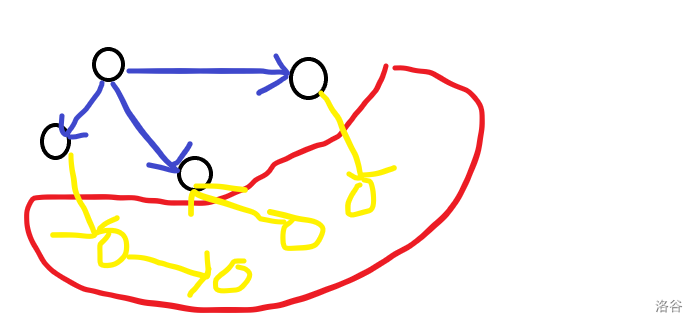
等下这个图是错的,要把最下面的黄点去掉。/kel
我们直接这样转移即可。
但是有问题啊,会算重!!!
还是上图的例子
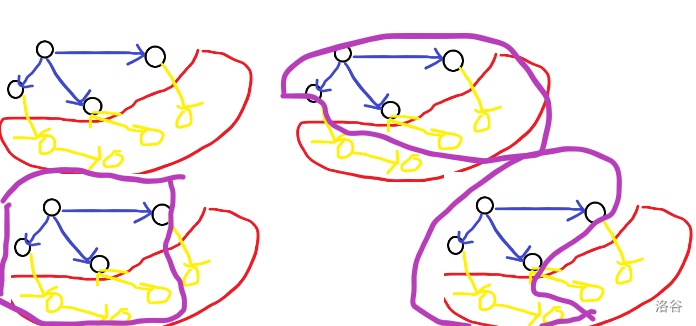
不难发现一个被算了很多次,我们直接容斥,如果互相独立的点的集合为奇数令他的贡献为正,否则为负。
写出来长这样:
找一个互相独立的点的集合可以这样:
rep(i,1,m){
int a,b;
cin>>a>>b;
G[a]|=(1<<(b-1));G[b]|=(1<<(a-1));
}
ok[0]=1;
rep(s,0,(1<<n)-1){
rep(i,1,n){
if(s&(1<<(i-1))&&!(G[i]&(s-(1<<(i-1))))) ok[s]=ok[s-(1<<(i-1))];
}
}
子集你肯定知道是 \(O(3^n)\) 的。
贺一个题解的话就是:钦定零度点集,简单容斥去重。
ABC306Ex
经典题*2
考虑没有等号怎们做,不就是上一个题吗?
那我们只需要考虑有等号的情况就行了,这个不就等价于缩点吗,预处理所有可能的情况,用并查集维护一下联通块大小,和上一个题没有区别。
拉插优化dp
难点在于想到拉插,可以看看这一篇是如何找到次数的。
省流:差分!!!
lsy给的题不多,经典题还是自己找一找。
Day 3 树上ds,图论相关 (lsy)
最开始有点 Trivial。
前面东西总结一下:
- 尽量使用基本的技巧,转化为经典问题
- 根据信息结构的强弱,使用不同的东西维护。
- 倍增维护等幂信息,这个只需要不漏,树上差分要想的起来。
重剖:candy。
长链剖分:我好像写过一点,但是还有优化 dp。
线段树合并:今天主要不是基础,是线段树合并优化 dp。
其他的总结是线段树合并+树上差分可以做到“在恰当的时刻拥有想要的信息”
还是写一下优化 dp 吧。
要满足一些条件,有用的值是 \(sz\) 个,并且后面那一坨是一堆相乘的形式。实际上是整体 dp。
dsu on tree:本身简单,今天讲的题有点抽象,一个 Trick 是枚举 LCA。
最小生成树:我们不一定要用,主要是 3 种求法的思想各有各的用处。
生成树相关构造与 dfs 树:dfs 树具有不存在横叉边的性质。
点双:圆方树,不解释/wx。
强连通性:今天学会了 kosaraju !!!,对于正图dfs,记录出栈时间戳,在反图从大到小 dfs。
耳分解
双极定向
2-SAT:今天的技巧是将 \(X_{i,j}=[a_i\le j]\) 作为条件。
欧拉回路:dfs,回溯时加入当前点。
这里是题解。
CF888G
考虑 Boruvka,注意:这一种题目中,我们往往只是借鉴了它的思想。
我们逐位进行考虑,对于在 \(w\) 这一位中,我们将 \(0\) 与 \(1\) 的分开考虑。
我们在一侧的 root 上面直接套用经典做法找到异或最小值,然后将 \(0,1\) 两侧的树合并即可,注意到这样的话权值还要加上 \(2^w\)。
CF1364D
把 dfs 树建出来,至于相关的东西,在图论杂题写过。
无向图 dfs 树是没有横插边的。
如果能找到合法环就找,不能直接找独立集。正确性显然。
Public Judge Round 3, A
考虑 Boruvka,我们对于中间的点,只能向上或向左连一条边,然后将最外面的边直接连起来。
UOJ176
Boruvka。
P8820
111
P4577
课上讲的是dsu on tree (记得哪天写一下这个)
我们考虑 dp,设 \(dp_{i,j}\) 表示 以 \(i\) 为根的这一棵子树,此时的选的最小值为 \(j\),
有以下转移
第一个正常的对每一个节点开一颗线段树,直接往上转移。
第二个考虑线段树合并优化,因为没怎么写过所以写的比较详细。
对于两颗线段树 x 和 y,我们进行分类讨论。
可以画图更有助于理解
维护 \(x\) 右边的 \(\sum\limits{dp_{v,\geq j}}\),叫做 \(maxp\) ,另外一侧叫做 \(maxq\)
1.\(x=0,y=0\) 直接返回。
2.\(x=0,y \neq 0\) 直接给 y 上的节点区间加 maxp。
3.\(x \neq 0,y = 0\) 直接给 x 上的节点区间加 maxq。
4.\(x \neq 0,y \neq 0\) 线段树合并上去。
int y1=t[rs(y)].val,y0=t[rs(x)].val;
ls(x)=merge(ls(x),ls(y),l,mid,max(maxp,y0),max(maxq,y1));
rs(x)=merge(rs(x),rs(y),mid+1,r,maxp,maxq);
对于左子树,我们要加上右子树的那一坨东西。
这个题对对于右子树,不需要管。
最后 dp 过程大概是这样的
void dfs(int u,int fa){
int val=1;
for(int i=h[u];i;i=g[i].nxt){
int v=g[i].v;
if(v==fa) continue;
dfs(v,u);
val+=query(root[v],a[u],Lim,0,Lim);
root[u]=merge(root[u],root[v],0,Lim,0,0);
}
modify(root[u],0,Lim,a[u],val);
}
P5298
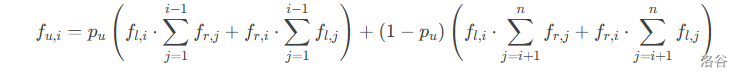
转移是这个,我们只需要维护前缀和,后缀和,我们考虑线段树合并优化 dp。
1.\(x=0,y=0\) 直接返回。
2.\(x=0,y \neq 0\) 直接给 y 上的节点区间乘 maxp。
3.\(x \neq 0,y = 0\) 直接给 x 上的节点区间乘 maxq。
4.\(x \neq 0,y \neq 0\) 线段树合并上去。
int merge(int x,int y,int sumx,int sumy,int pbmax,int pbmin){
if(!x){mktag(y,sumx);return y;}
if(!y){mktag(x,sumy);return x;}
pushdown(x),pushdown(y);
int x0=t[ls(x)].val,x1=t[rs(x)].val,y0=t[ls(y)].val,y1=t[rs(y)].val;
ls(x)=merge(ls(x),ls(y),(sumx+pbmin*x1)%mod,(sumy+pbmin*y1)%mod,pbmax,pbmin);
rs(x)=merge(rs(x),rs(y),(sumx+pbmax*x0)%mod,(sumy+pbmax*y0)%mod,pbmax,pbmin);
pushup(x);return x;
}
CF1697F
难点在于想到2-SAT。
Trick:将 \(X_{i,j}=[a_i\le j]\) 作为条件。
CF1583H
你管这个叫 *3300?
第一问从大到小加入,用并查集维护。
第二问就则略微不同,我们考虑如何合并两个集合,如果最大值不相等直接并查集完事,如果相等,我们可以在两边的集合中取 max,但是还有中间的东西,但我们只需要求最大费用就可以,所以随便找一条路径,取一个最大值就行了。这种做法相当于建了隐式的重构树。
长链剖分的题
看到我记得让我催更
连通性相关题目
看到我记得让我催更
Day 4 ds lyc
是不是最开始没讲的部分才是最有趣的
最开始就是经典的矩阵规约。多头是不是讲的有点水
四毛子: 实际上是 log 分块。
这里只有 +1-1RMQ。
我们取一个阈值 \(B\),一共有 \(\dfrac{n}{B}\) 个块,然后对于整块直接维护 \(\dfrac{n}{B}\) 个ST表,这个是 \(O(\dfrac{n}{B} \log \dfrac{n}{B})\) 的。
实际上,我们研究一下本质,实际上我们要解决的问题是,如果两个点在一个块里面,我们如何求出最值,因为不在一个 块时,维护前后缀就可以了,我们需要充分利用好性质,对于长度小于等于 \(B\) 的长度,我们注意到一共只有 \(2^{B}\) 种可能,总的复杂度是 \(O(B 2^B)\) 的。令 \(B= \frac{\log n}{2}\) ,此时是线性的。
讲 \(𝑘\) 叉树 是不是还是有点魔怔了,我是不是直接可以取 \(e\) 的到理论最优复杂度。
接下来并不是 PPT 上的内容。
我们考虑维护 ds 我们要干什么。
1.信息的性质,例如结合律,以及前几天 feecle 讲课提到的那些。
2.靠近经典问题。
3.在线,离线,注意:这个和我们平常说的强制在线之类的是有区别的。,真正的在线的东西只有二分,但是好像不止吧,好吧实际上还有自动机的构造,例如莫队指针的偏移,我们需要查询一些信息,用来统计答案,这些东西显然不是强制在线的,所以我们在离线把这些信息处理,这就是所谓的“二次离线”。
4.势能,看下面。撤销:e.g. 可撤销并查集,线段树分治,回滚莫队。
根号分治:今天讲的题目难点不在于这个,之前有过总结就不写了。
势能分析:这应该是比较正(che)统 (dan)的。
经典问题:区间开根,区间和。
sol:我们的势能是区间 max。每一次向下开根,都会变小很多。
同样是经典问题:区间开根,区间和,区间加。
sol: 令势能 \(\sum \log(\log |a_i-a_{i-1}| +1)\)
不要看上去很吓人,实际上很多都是类似形式。
1.若势能为 0,即区间所有数相同,实际上还要特判极差为1的情况,无须递归下去开根;
2.若递归下去开根了,区间的势能至少 −1;
3.每次区间加,势能增加是 \(𝑂(\log \log n)\) 的。
所以只需维护区间是否相同。
减半报警器:。
这里是题解
莫队二离
模板题
首先暴力莫队过不去。
我们考虑将 $\left[L,R\right] \to $ 其他地方的贡献算上。
将\(\left[L,R\right]\) 对 \(x\) 的贡献记作 \(g\left(L,R,x\right)\)
- $ \left[L,R \right] \to \left[L,R+k\right] $
就是求对于在 \(\left [R+1,R+k \right]\) 的 \(x\),求出 \(g(L,x-1,x)\)
差分之后就是 $g(1,x-1,x) - g(1,L-1,x) $,前面的东西,我们可以直接算出来,而后面的东西,我们再次离线,就像这样给他打上一个标记
g[L-1].push_back({R+1,q[i].r,-i});
同理我们可以写出整个过程。
P3350
dp选讲写过了。
P8564
树上背包,我们可以采用上下界优化,做到 \(O(n^2)\) 的复杂度。
区间推max/min
维护最大值,次大值,最大值次数。
Day 5 flow,分治 (lsy)
原来的 blog 写了一点基础问题。
上午的题目非常的有意思。
CF1250K 这个题告诉我们一些事情,我们可对于网络流问题,我们第一个点是找到一个非常容易的数学模型,第二个是对于一个结论,可以猜测必要性推测充分性。
CF1684G 这个题也是找到一个非常容易的数学模型,如果找到了这个题建二分图是非常自然的事情。
P4003:费用流入门题目,注意力惊人。
Primal Dual 算法:实际上是势能 dijkstra,可以看看以前写的。
费用流问题,每一单位流量的最短路长度单调不减。
最小割的实质:假设 \(x_i\) 表示 \(i\) 是不是和 \(S\) 在一边,则目标就是最小化
注意:问题只能转化成这种形式,否则是 NP-hard的
题目非常有意思,后面放上来。
模拟网络流,费用流
P5470:模拟费用流入门题。
建图之后要大力分类,感觉挺抽象的。
下午的题目还是很有有趣的,感觉 PPT 写的很详细,等我做了在放上来。
这里是题解。
我好像有些不会做。
CF1684G
好题。
我们考虑怎们构造,因为这个和上课内容无关,所以我们直接写了。
对于 \(t_i \leq \dfrac{m}{3}\),直接构造 \((3m,2m)\) 就可以了。
对于 \(t_i > \dfrac{m}{3}\),最优秀的构造是 \((2p+x,p+x)\),其中 \(p> \dfrac{m}{3}\),\(x < \dfrac{m}{3}\),这个代表对于一个 \(p\),至少需要一个 \(p\) 去与它匹配,还要只产生这两个数。判断一下是否同余。然后建立二分图跑一个二分图匹配就行了。
P8215
最小割模板题目。
变量是什么:每个人参与或者不参与,每个团队愿意或者不愿意。
对于第一个限制。直接 \(S\) 向 \(i\) 连 \(d_i\),\(i\) 向 \(T\) 连去 \(c_i\)。
真的按上课那个套路感觉没什么难度,懒得写了。
P3227,P6054
别急。
P4313
把所有贡献减去最小割。
真的按上课那个套路感觉没什么难度,懒得写了。
AT_arc142_e
前置:二分图最大权独立集:求二分图最大权值和的独立集。
先设 \(x_i\) 表示 \(i\) 选不选,然后把一边的变量取反。
伟大,无需多言。
这个是真的困难。
我们实际上的限制是
后面那个拆开之后实际上是
直接调整就可以了。
切糕和一些 2-SAT 的题目告诉我们我们题目的变量可以是形如 \(X_{i,j}=[a_i \leq j]\) 的东西是可以作为变量的。我们尝试直接做,但是条件是 \((\lnot x_{i} and \lnot x_{j})\) 并不能直接做,所以这个题做不了
观察一下,如果有一个下界已经 $ \geq \max(𝑏_x,b_y)$ 就不用考虑了。
如果没有了,这个限制意味着什么,我么要让其中一个东西大于$ \geq \max(𝑏_x,b_y)$,这个东西好像对于一组限制,就已经是二分图,对于左侧的,就是 \(a_i<b_i\),另外一侧是 \(a_i \geq b_i\),我们直接转换成为 \((x_{i} and \lnot x_{j})\),好了这个就是二分图的形式。
不要急,我们还没有考虑每一个变量的限制。
有一个显然的东西是$i+1 \to i $ 连接 INF。
不是剩下的都很显然啊,不写了。后面就是上课讲的基础东西。
AT_arc125_e
CF1442D
有意思的。
我们注意到最优的选择一定是只有一个没有选完,其他的都选完了。
暴力 dp 是枚举只有一个没选完的点 \(x\),将 \(1,2,3,\dots x-1,x+1,\dots,n\) 加入 dp,这个是 \(O(nk^2)\) 的。
考虑分治,solve(l,r) 这个东西表示已经将 \(\left[1,l-1\right] \cup \left[l+1,n\right]\) 的东西加入了背包,那对于 \(solve(l,mid)\),我们只需要将 \(\left[mid+1,r\right]\) 加入背包,回溯是回退即可。
solve(l,l) 就是答案。
P7482
没有意思题。
直接暴力维护 \(4\) 个 dp 数组,分别为左端点可以选或一定不选的的独立集,右端点可以选或一定不选的的独立集。然后分治算贡献就行了。
P4755
最值分治,很有趣的套路,如果贡献和最值相关,我们直接对最值进行分治,每次只需要枚举小区间,算它对大区间的贡献,感觉你可以叫他启发式分裂。
P5654
以后我一定要学会线性求笛卡尔树!!!
考虑将询问拆开,我们以左端点为例,对于 \(\left[l,r\right]\) 这个点,从\(\left[w+1,r\right]\) 来的的贡献不改,只需改另外一侧就行了,只需要ds维护就行了。
P9058
遇见树上路径问题,考虑点分治。
那们直接转化为 \(dis_u+dis_v\) 就是对的,但是这样的点对太多,很多都没有用,他们可以被其他东西偏序掉,这个东西就叫做支配对。
在这个题目中,我们只需要找到他们的前后继就行了,一共只有 \(O(n \log n)\) 个,用单调栈维护,最后是一个类似二维数点的形式,代码并不难。
P5979
feecle:这个题很简单,我们就不讲了。
P2305
出栈序+李超线段树套线段树
CF1373F P6122 P3826 P4214 P3980 CF1427G CF1666K P1792 CF2029I
还没有看。
Day 6 纸糊串
我会哈希,你会吗。
内容和这个高度重合,看看这个吧。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号