字符串基础
搬一下
upd on 25.7.10:增加了 SAM，对原来的部分内容进行了重构，增加了一些理解。
再不写就要忘完了。
给自己看的。
一些前言：
OI中的字符串算法实际上只有两种，第一种的原理是通过我们原本处理的序列信息，得出新的信息。第二种是建立自动机，分析自动机的性质得出结论，总之，就是通过已知的信息，得到新的东西。
hash
这个还是会的。
void init(){
p[0]=1;rep(i,1,n){p[i]=p[i-1]*P;hs[i]=hs[i-1]*P+s[i]-'a';}
}
ull gv(int l,int r){return hs[r]-hs[l-1]*p[r-l+1];}
KMP
比较基础，现在应该彻底弄懂了。
我们需要求：字符串 \(S\) 前缀的最长 Border，就是 next 数组。
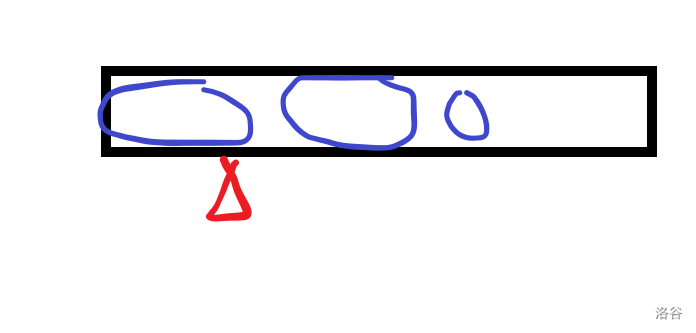
假设我们现在在最后一个蓝点 \(i\)，我们原来的指针在红点 \(j\)，我们看一下 \(S_{j+1}\) 等不等于 \(S_{i}\)，等于的话往后直接 j++，否则继续往前面跳，跳指的是 \(j=next_j\)。
这个东西虽然很基础，但是这给我们带来一些思考，字符串的很多优化都是基于前面已经算出的东西，进行下一步操作。
Trie
简单，但是有一些经典Trick蛤。
Manacher 和 Exkmp
这两个东西放在一起，是因为他们本质实际相同。
参考了魏老师的字符串blog。
Manacher：求一个字符串的最长回文串。
首先为了避免讨论，将它中间插入字符，例如\(S=\mathtt{aabbccdd}\)，变为\(S=\mathtt{a @ a @b @b @c @ c @ d@ d}\)
考虑枚举回文串中间的点，我们直接向两边扩散，这个是 \(O(n^2)\) 的，不能通过。
实际上我们在之前已经算过了很多内容，由于回文的对称性很多都是算过的，我们记录我们目前最远算到的位置,如果小于，根据对称性，我们可以画一下图
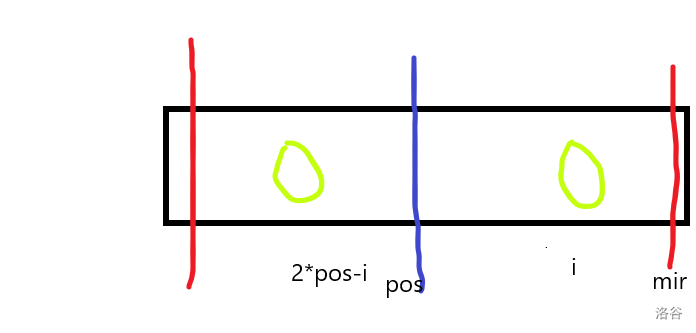
所以第 \(i\) 处的答案就可能是 \(2 \times pos -i\)，然后与有边界取一个 min
int manacher(){
string res="|&";
rep(i,0,str.size()-1){res+=str[i];res+='&';}
int pos=0,ans=0,mir=0;
rep(i,1,res.size()-1){
p[i]=(i<mir)?(min(p[2*pos-i],mir-i)):1;
while(res[i-p[i]]==res[i+p[i]]) p[i]++;
qma(ans,p[i]-1);
if(i+p[i]>mir) mir=i+p[i],pos=i;
}
return ans;
}
Exkmp：主要是字符串与字符串的每一个后者的最长公共前缀。
类似马拉车，我们可以即当前前缀匹配的区间为\([L,R]\)，紧接着我们可以暴力向后匹配。
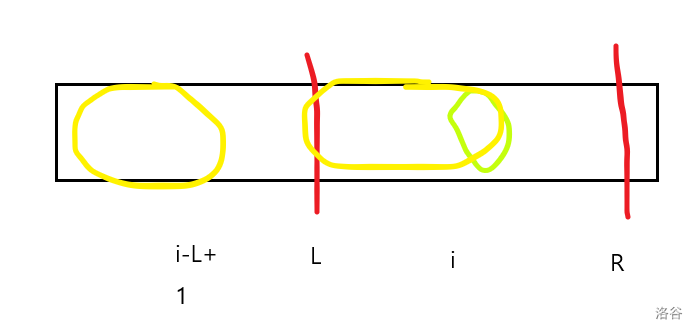
z[1]=m;
for(int i=2,l=0,r=0;i<=m;i++){
z[i]=(i>r)?0:(min(r-i+1,z[i-l+1]));
while(T[1+z[i]]==T[i+z[i]]) z[i]++;
if(i+z[i]-1>r) l=i,r=i+z[i]-1;
}
for(int i=1,l=0,r=0;i<=n;i++){
p[i]=(i>r)?0:(min(r-i+1,z[i-l+1]));
while(p[i]<m&&T[1+p[i]]==S[i+p[i]]) p[i]++;
if(i+p[i]-1>r) l=i,r=i+p[i]-1;
}
AC自动机
什么是自动机：Eg:Trie树。
\(\mathtt{S:用来建立自动机}，\mathtt{T:用来喂给自动机}\)
我们尝试去构造啊，先把所有的东西放到一个 Tire 树上，类似与 KMP，我们尝试去失配啊，我们考虑一个 Tire 树的结构，如果我们向下 bfs 的时候，有一个是找到了，我们直接就跳到 \(fail_u\) 下面就行了，否则，我们直接让他联系到 \(fail_u\)。
Fail Tree：有一个经典结论，把所有 S 建立起来，然后我们一直跳 T (在 fail 树上)，给它做一个+1，最后在查询最后一个点的子树和，就是出现次数。
namespace ACAM{
int tr[N][26],tot=0,fail[N*26];
void insert(string str,int id){
int u=0;
rep(i,0,str.size()-1){
int now=str[i]-'a';
if(!tr[u][now]) tr[u][now]=++tot;
u=tr[u][now];
}
}
void getfail(){
queue<int>q;
rep(i,0,25){if(tr[0][i]) q.push(tr[0][i]);}
while(!q.empty()){
int u=q.front();q.pop();
rep(i,0,25){
if(tr[u][i]){
fail[tr[u][i]]=tr[fail[u]][i];
q.push(tr[u][i]);
}else tr[u][i]=tr[fail[u]][i];
}
}
}
}
SA
不嘻嘻
咕咕。
void qsort(){
rep(i,0,M) tax[i]=0;
rep(i,1,n) tax[rnk[i]]++;
rep(i,1,M) tax[i]+=tax[i-1];
atrep(i,1,n) sa[tax[rnk[tp[i]]]--]=tp[i];
}
void SA(){
M=128*128;
rep(i,1,n) rnk[i]=(int)s[i],tp[i]=i;//初始化
qsort();
for(int w=1,p=0;w<=n;M=p,w<<=1){// w /to 2w
p=0;
//第二关键字排序
rep(i,1,w) tp[++p]=n-w+i;//从n-w+1 一直到 n
rep(i,1,n) if(sa[i]>w) tp[++p]=sa[i]-w;
qsort();//第一关键字排序
swap(tp,rnk);//剩下的交换，没用
rnk[sa[1]]=p=1;
rep(i,2,n){
rnk[sa[i]]=(tp[sa[i-1]+w]==tp[sa[i]+w]&&tp[sa[i-1]]==tp[sa[i]])?p:++p;
}//去重
}
rep(i,1,n) cout<<sa[i]<<" ";
}
SAM
接下来的东西我觉得多头不会SAM认识非常深刻。但是太抽象了，写一点自己的理解。
我们需要让它干什么：维护后缀信息。
怎们做：Trie 树，把所有后缀插入进去，复杂度是 \(O(n^2)\)
我们如果能把自动机（前面说过，Trie 树也是自动机），让他的边和点数量尽量的少，我们就达到任务了。
Endpos:对于一个字串 \(p\)，它在原串出现的右端点的集合。后文我们记为 \(\mathrm{endpos} (p)\)
Lemma 1：对于两个子串 \(\mathrm{p,q}，\mathrm{endpos} (p)=\mathrm{endpos} (q)\)，\(\mathrm{|p|}<\mathrm{|q|}\)，\(\mathrm{p}\) 是 \(\mathrm{q}\) 的后缀。
Lemma 2.1：对于两个子串 \(\mathrm{p,q}\)，要么 \(\mathrm{endpos} (p) \in \mathrm{endpos} (q)\)，要么\(\mathrm{endpos} (p) \varnothing {endpos} (q)\)
Lemma 2.2：在 Lemma 2.2 的基础上，同一个，我们将 endpos 完全相同的字串，放入一个集合，我们叫这个东西 endpos 等价类，同一个等价类中，字符串的长度大小是连续的。
你能够发现，我们能用 endpos 这个东西去描述子串的结构。这个就是多头 PPT 上的内容的意思。
Lemma 3：endpos等价类个数的级别是 \(O(n)\)。
Proof：没必要。
。
接下来我们根据引理3，我们将 endpos 等价类这个东西，建立一棵树（实际上也是自动机）例如\(\mathrm{S}=\mathtt{aababa}\)的 parent 树如下图（这个东西我觉得我不好描述）：
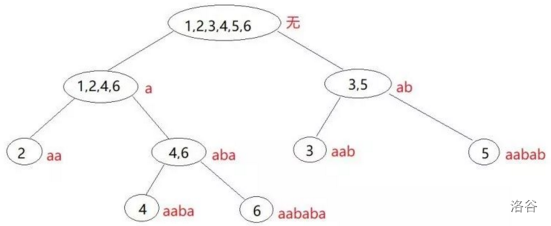
我们现在可以开始构造自动机了，根据前面说的，我们实际上是维护 endpos 等价类产生的 parent 树，并且让他成为一个自动机的形状。
我们自动机的构造是在线的。所以我们不妨考虑将 \(\mathrm{S_i}\) 这一位加进去会发生什么。
先咕咕了。
构造的事情不重要，记住一个东西，自动机从上到下，parent 树从下到上。
浙公网安备 33010602011771号