手撸 Pandas - 01：Numpy，基础可视化，聚合，标准差

导入需要的模块，相应数据下载地址：https://grouplens.org/datasets/movielens/

import pandas as pd
import time
import os
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

为了看一下Pandas的效率，这里计算了要处理文件的大小，以及load文件所需要的时间。结果显示，对于一个509Mb的csv文件，加载时间只需要8秒，效率还是比较高的。通过Pandas加载的数据会被转化成Dataframe的数据结构，其底层是Numpy的Array。

同样可以使用ipython的魔术命令来计算时间

Pandas 与 Numpy 关系：

~ Pandas的基本结构为Dataframe，也就是上面这种行列坐标合成的表的形式，其中每一列 'userId', 'movieId' ... 都是一个Series，Series底层就是Numpy的array。

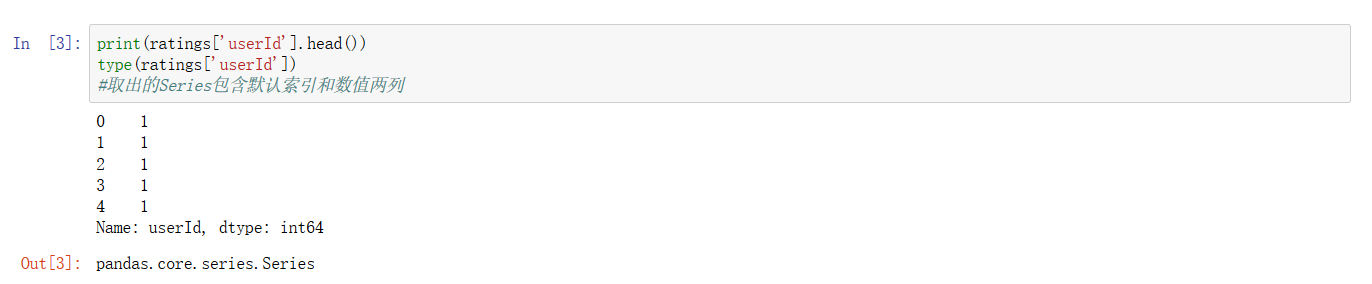
~ 通过切片的方式，可以从Dataframe中直接取出Seires。

对Series取值，得到的就是Numpy的array

用 index 获取 Pandas 的索引，得到的是一个 Pandas.Range 对象，通过 tolist() 方法，就可以得到一个列表

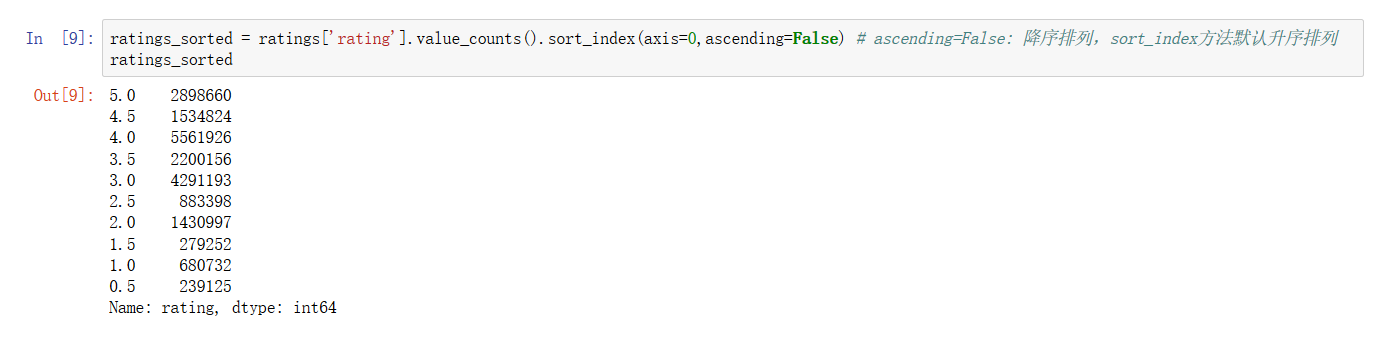
通过 value_counts() 可以对 Series 进行统计，我们对 rating 评分列做一下统计，可以看到每一个评分的总数都有统计，网站电影5.0的评分，总计有2898660个，4.0的评分，总计有5561926个，此站电影质量总体还不错

但是仔细看下，value_counts() 返回的 Series 是按照value的降序排列的，而 index 的顺序是混乱的，Pandas 提供为 index排序的方式

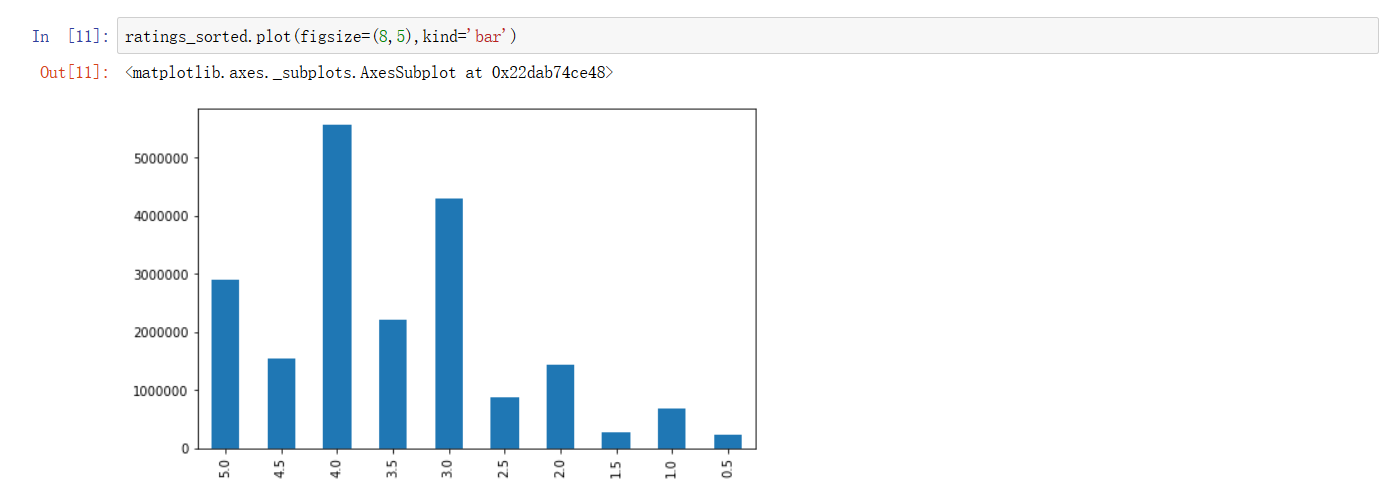
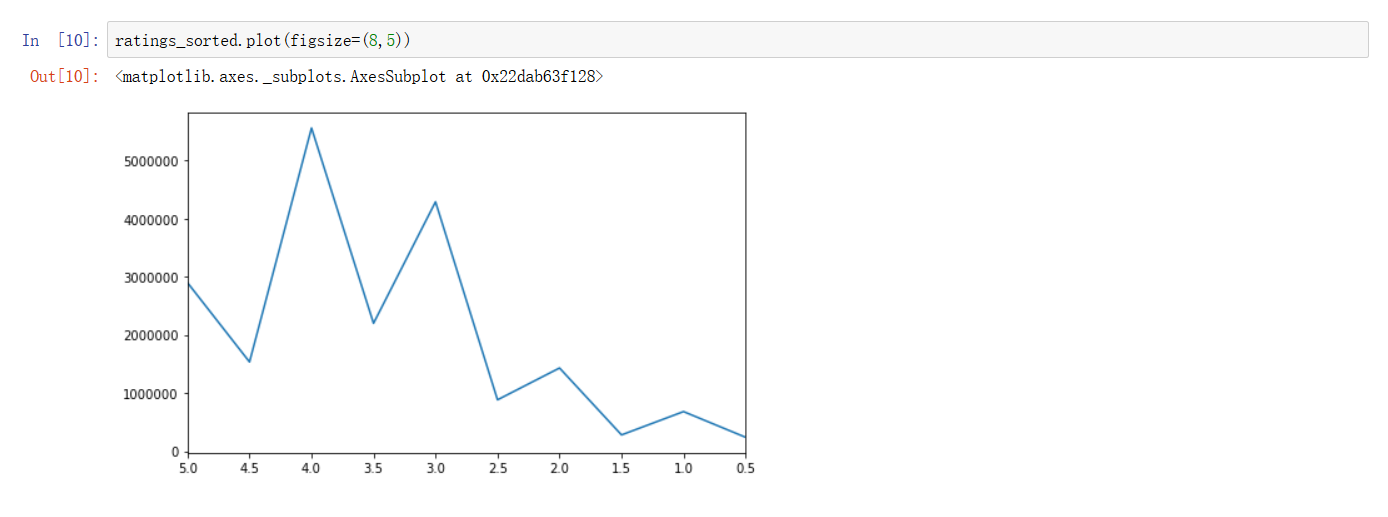
一图胜千言，看一下评分的数据，进行可视化之后是什么样子？横坐标是评分，纵坐标是该评分的总数，Pandas 的 plot方法，默认为折线图。貌似折线图不符合我们的高逼格期待，可以通过设置 kind 参数，调整可视化模式。

调整后的直方图，看起来逼格就高很多啦！也可以将横纵坐标颠倒，看上去与很多科学期刊上的图更像呢。

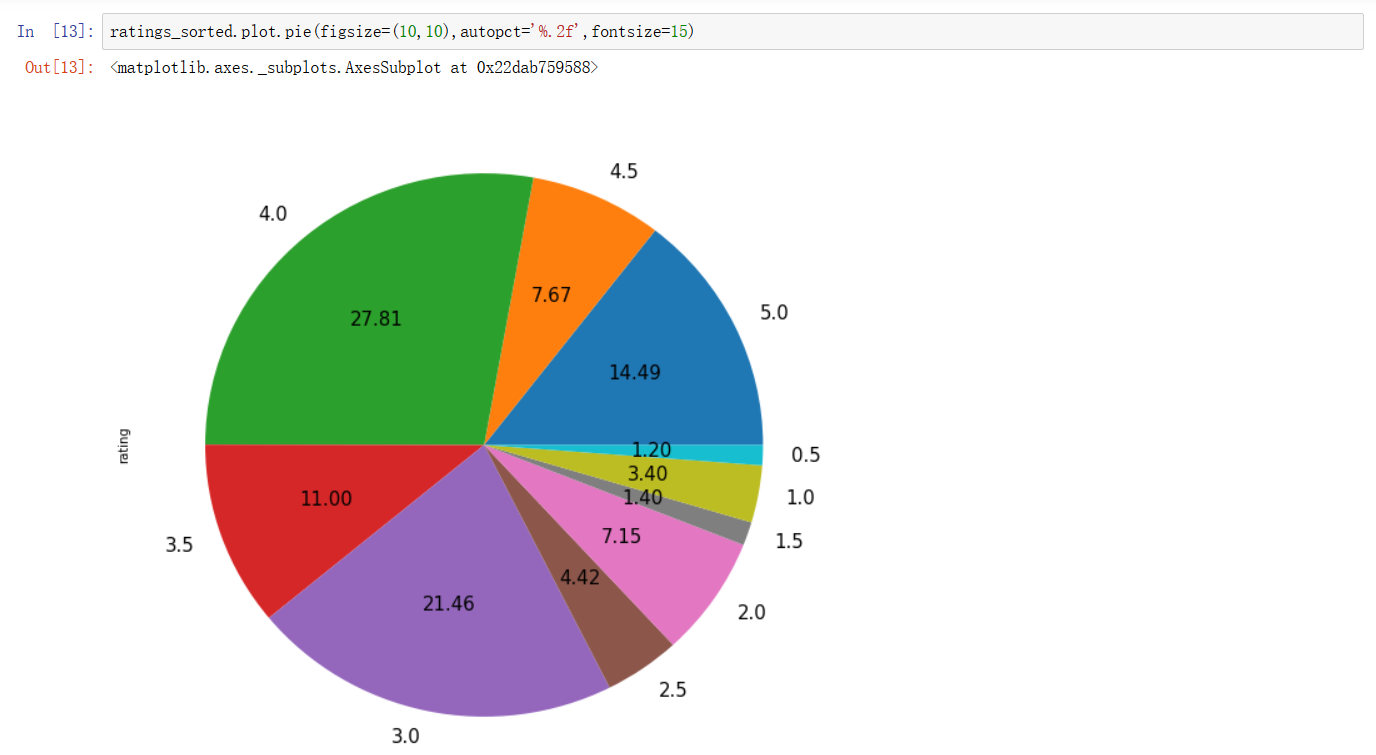
逼格更高的我们还可以画个饼，设置 autopct 参数来标注相应的占比，嗯，Pandas 看上去的确不错，兼顾了逼格与易用性

通过 Pandas 还可以画一种“密度图”，密度图是通过计算可能会产生观测数据的连续概率分布的估计而产生的。一般过程是将该分布近似为一组核分布，因此，密度图也被称作KDE（Kernel Density Estimation）图，调用plt时加上kind='kde'就可以生成一张密度图。最常用的内核是高斯核（在每个数据点产生高斯钟形曲线）。

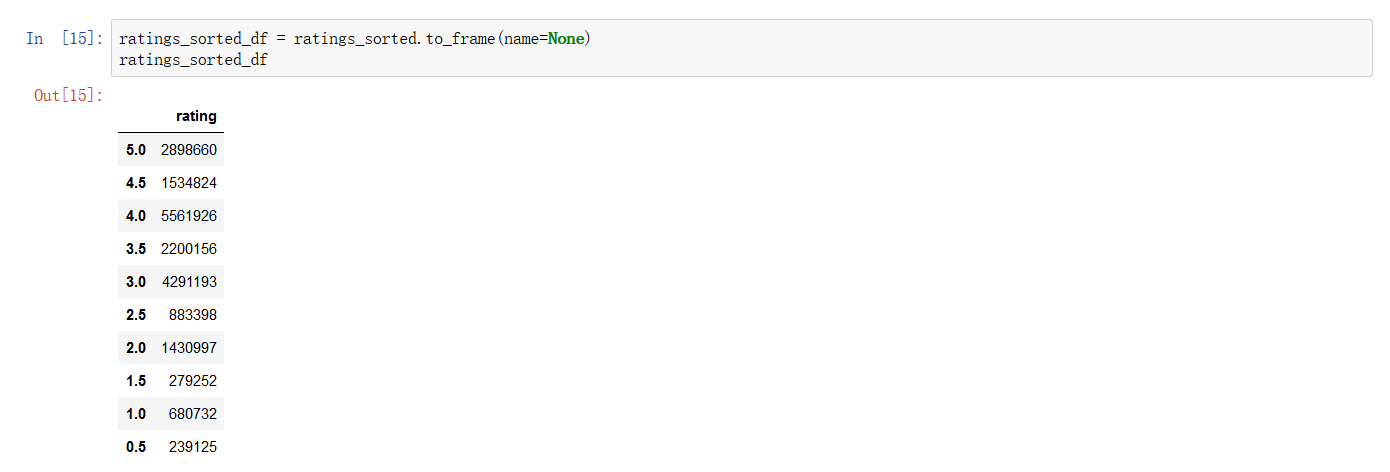
通过 Pandas 还可以绘制“散点图”（kind = 'scatter'），由于散点图只能用于 Dataframe，所以要先将我们的 Series rating_sorted 转化为 Dataframe。

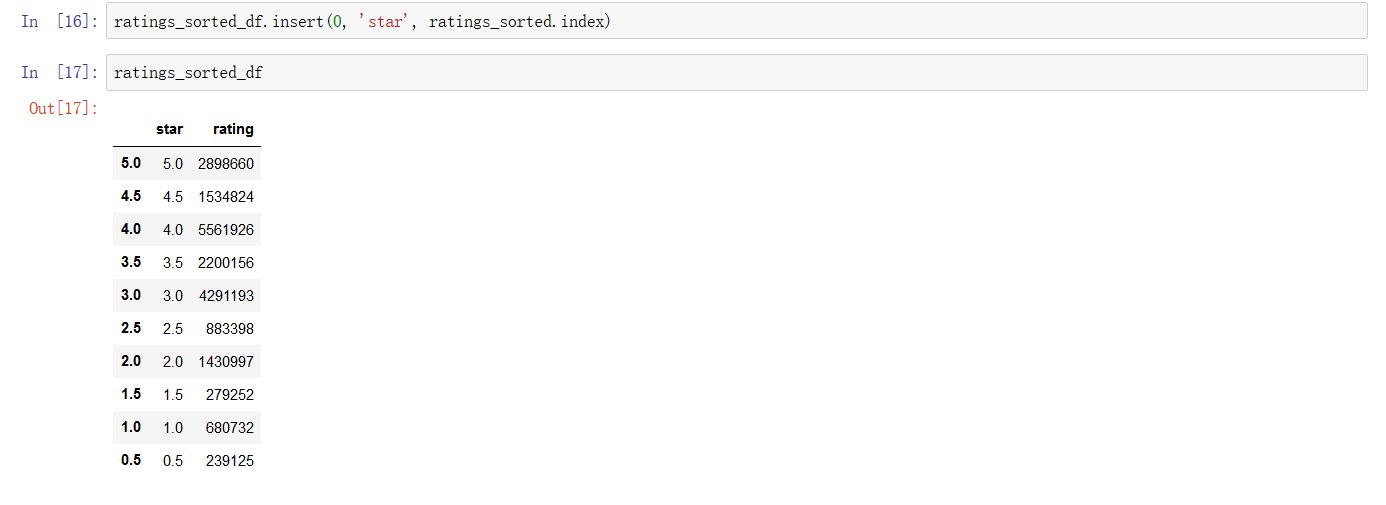
散点图需要设置两个参数 x 轴与 y 轴，分别对应 Dataframe 中的列名，所以我们要在 rating_sorted_df 中添加一列，也就是把我们的 index 转化为 Dataframe 中的一列，取名 'star'：星

一切准备就绪，可以画图了，虽然在这里散点图没有什么实际意义x_x

通过 Pandas 可以将两个数据库非常方便的合成新数据库。

我们先来看看Movie这个数据，小文件，秒载入。这是关于电影信息的一个数据库，包含 movieId，电影名 title 和电影类型genres。

通过 Pandas 的 merge 方法，可以自动锁定合并表格的 key 值，在这个例子中，两个表应该是以 movieId 为键值进行合并的，合并时间为5s

Pandas 提供了一个灵活高效的 groupby 功能，用于数据聚合与分组运算，如计数、平均值、标准差，或用户自定义函数。其原理根据一个或多个键（可以是函数、数组或 DataFrame 列名）对 Pandas 对象进行拆分。

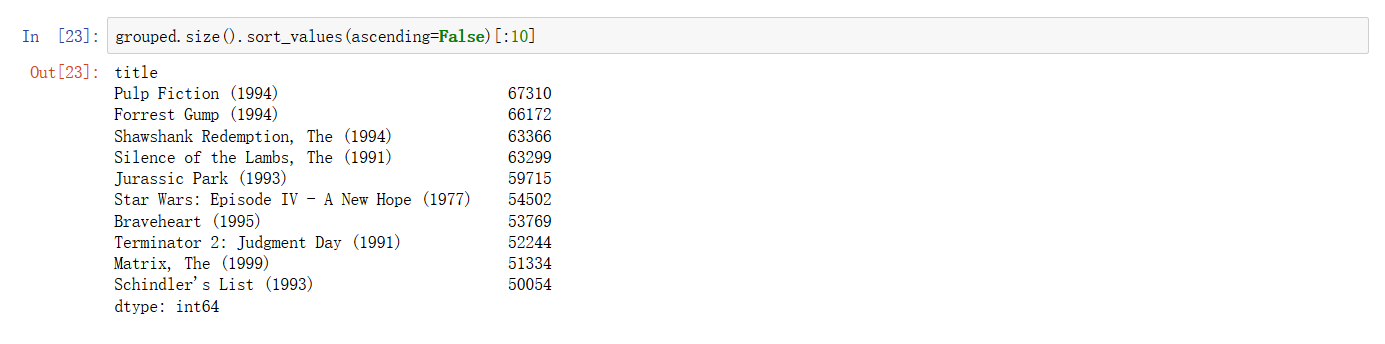
这里看一下，按照 title 聚合之后，统计一下每个电影获得评分的数量，并按照降序排列，获得评分数量最多的电影就应该是最受欢迎的电影啦~~ 嗯，第一份数据分析工作就要获得成功了！想想就开心哦！

通过排序我们可以从数据中获得一些有用的信息，Pulp Fiction（低俗小说）获得了最多的评分数量，but wait a minute!低俗小说... 貌似是一部口味很重，情节恶心的电影！虽然它获得了最高的评分数量，但这就能说明它是最受欢迎的电影吗？

既然我们对这部电影是否受欢迎产生怀疑，那么我们可以通过计算该电影评分的方差或标准差来判断，大众对这部电影对评分是否一致！groupby 提供一个计算标准差的函数 std

嗯，结果果然像预计的一样，这部电影标准差达到了 0.976，公众对于这部电影的分歧还是蛮大的哦！

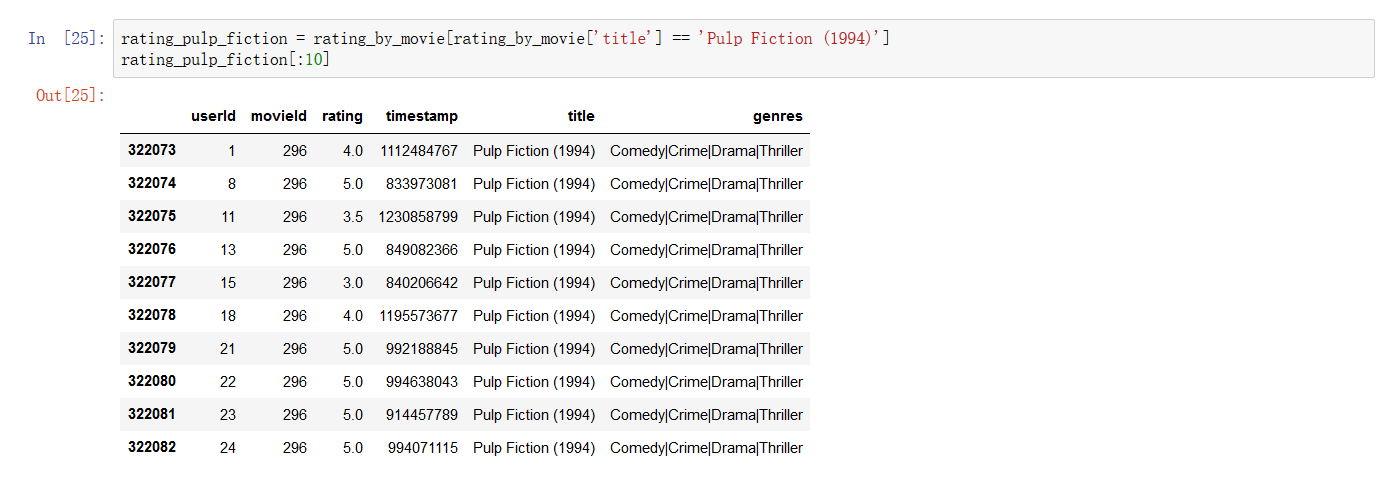
很好奇哦，这部电影的分歧到底有多大呢？

统计 rating 的分数来看，绝大多数的评分都是在3星以上，看来大众的口味还是比较一致的???

我们还可以来看看分歧最小的电影长啥样？找出标准差小于0.1的电影