测绘线性代数(五):测量平差中的虚逆
到目前为止,有熟悉的3种分解:
1. A n*n= Ln*nUn*n分解,针对【可逆】【方阵A】。L为下三角可逆方阵,U为上三角可逆方阵。
2. An*n = Qn*nRn*n分级,针对【可逆】【方阵A】。Q为单位正交矩阵,R为上三角可逆方阵。
3. An*n = Sn*n∧n*n S-1 ,针对【任意】【对称】【方阵A】。S为A的【特征(列)向量】阵,∧为【特征值】对角矩阵。可以简化为A = Q ∧‘QT ,Q为单位正交矩阵。
4. Am*n = Um*mΣm*nVn*nT,针对【任意】 矩阵A。 U是AAT 的【特征向量可逆单位方阵】,Σ是AAT 的特征值开根号,V是 ATA 的【特征向量可逆单位方阵】。
5. Am*n = Bm*rCr*n,针对【任意】 矩阵A,满秩分解。 R(A)=R(B)=R(C)=r B为列满秩,C为行满秩。满秩分解的定义、证明、求法(矩阵分解——1. 满秩分解) - 知乎 (zhihu.com)
满秩分解
A = Bm*rCr*n,是基于A = UΣVT的。
因为∑的对角线是 √λ 值或0。那么将∑分解为:
Er*r 0r*(n-r)
0m*m-r 0(m-r)*(n-r)
那么,A就变为:
A = U * [E,0]T [E,0] VT
B = U * [E,0]T
C = [E,0] VT
注意,这样的B、C不是唯一的。
求解BC:满秩分解的定义、证明、求法(矩阵分解——1. 满秩分解) - 知乎 (zhihu.com)
左右逆矩阵
B为【列满秩】,所以存在【左逆】
BL-1=(BTB)-1 BT 【列满秩】时,BTB为n*n矩阵可逆,因此 I = BL-1 *B。证明见:测绘线性代数(一):基础 - 耀礼士多德 - 博客园 (cnblogs.com)
同理,C为【行满秩】,所以存在【右逆】
CR-1= CT(CCT)-1 , I = C * CR-1
广义逆A-
广义逆是满足:Am*n A-n*mAm*n = A 的所有A- ,A-不一定是唯一的,除非A为可逆方阵
A- = CR-1 * BL-1
代入:AA-A = (BC)(CR-1 * BL-1 )(BC) = BC = A 得证明
因为B、C不是唯一的,所以 CR-1 、 BL-1 、不唯一,因此A-不唯一。
那么:求A-的问题,变为了求B、C的问题。
伪逆A+
伪逆A+,是广义逆的一种,除了满足AA+A = A外,还【满足条件】:
(AA+)T=AA+、A+AA+=A+、(A+A)T=(A+A)
而且【只有一个】
(证明:《自由网平差与变形分析》P192)
(1)当A为任意阵,求解广义逆,见:测绘线性代数(三):伪逆解 - 耀礼士多德 - 博客园 (cnblogs.com)
A+ = VΣ+ UT ,V、U使用SVD分解。(证明:略)
而 I = A+ A = VΣ+ (UT U)ΣVT
所以 I = Σ+ Σ ,因为Σ是 √λ 值或0,所以Σ+ 为 1/ √λ 或0。
(2)当A为【对称方阵】。
A+ = A(AA)-A(AA)-A,证明:将这个式子代入,均【满足条件】。
因此,A+ 的问题,转化为求解(AA)- 的问题,转化为变为了求B、C的问题。
设有方程组 :
Ax = b
m行n列
*假设A为任意的形式(m>n,或m<n)。在测量的时候,通常是有m ≥ n(也就是观测方程个数 > 参数个数,例如水准测量、三角导线存在对测的情况)
*此处假如没有起算数据,那么Rank(A) < min(m,n),通俗说,就是线性无关方程数 < 参数个数
如果有:
x = A-b,那么认为x是【其中一个】解。
之所以说,是【其中一个】,A- 可能有很多个。因为A- 可能有很多个,所以x自然有很多个。
因为A+,【只有一个】。
x = A+b,就是【最小范数解】,其实就是满足洗个∑||xi||² 最小的解。(至于为什么,暂时不知道)
最小二乘 + 最小范数解
当有Ax = B,b不在A的列空间。
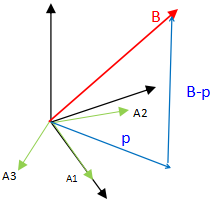
p⊥(B-p) ,所以,pT(B-p) = 0。有 p = AX(p可以由A各列线性组合得到),所以:
(AX)TB = (AX)T(AX)
XTATB=XTATAX
ATB=ATAX
ATAX = ATB,因为R(A) < min(m,n),所以ATA无逆。
问题转化:
ATA = N(N是对称方阵)
ATB = b
N X = b,那么最小范数解为:
X = N+b
通解、特解
齐次线性方程组Ax = 0和非线程方程组的 Ax = b
方程组Ax = b的解,可以理解为:
Ax = 0的解 x0 ,加上 Ax = b的解 xb
因为 A(x0+xb) = b,好像x0 很多余,没什么意义。
但是仔细看,x0 + xb 恰好是向量相加。
如果A可逆,那么x0 唯一,只能为0(想象一下,三维空间中,两个线性无关的向量形成一个平面,第三个向量不能在平面上,这3个向量要组成0向量,只能都乘以0)
x0 唯一,那么xb 也只能唯一,x0 + xb唯一,且等于xb
如果A不可逆,x0 + xb不唯一, 解的空间,可以看成所有x0和所有xb的线性组合。
而无论b是什么(可能是c、d、e、f),x0 部分都是固定的。
因此对于不可逆A,x0 有特殊意义。
为什么伪逆A+ 能满足最小范数解?
假设有线性方程组AX=B,其解为Y,那么:
AY = B
假设任意一个广义逆A-,广义逆满足:AA-A = A
AA-(AY) = B
A(A-B) = B
最终,其中一个A- ,对应其中一个X:
X = A-B
又有AX=0的一般解:X = (I - A-A)M (先不管M是有什么用的,M就是一个象征,令 A可逆时X只能为0,A不可逆时X可以不为0就行,即A-A ≠ I )
AX = A(I - A-A)M = AM - AA-AM = 0
所以AY = B的通解:
X = A-B + (I - A-A)M
在误差方程V = Ax - l ,满足 最小二乘VTPV= min 的情况下,解方程:
ATPAx = ATPl,令ATPA = N,原方程等价于:
Nx = ATPl(其中N是对称,因为P是对称的,所以ATPA对称,所以N对称)
X的通解为:
X = N-ATPl + (I - N-N)M
假设Nm-为使得||X||最小的一个广义逆,对应的特解有:
NY=ATPl
Y = Nm-ATPl,因为||Y||是最小的,所以:
||Nm-ATPl|| ≤ || Nm-ATPl + (I - Nm-Nm)M ||
(其中一个解的长度,少于其对应的所有通解的长度)
等价于:
||Nm-Y|| ≤ || Nm-NY + (I - Nm-N)M ||
左右平方一下(因为左右都是向量,所以相当于向量自己求内积,即乘以其转置)
得到:
0 ≤ MT (I - Nm-N)T (I - Nm-N)M + 2 YT(Nm-N)T (I - Nm-N)M
显然,MT (I - Nm-N)T (I - Nm-N)M是一个向量的长度平方,肯定是大于等于0的,因此,要此式子恒成立,必须:
(Nm-N)T (I - Nm-N) = 0
所以,Nm应该满足:
(Nm-N)T = (Nm-N)T Nm-N(有一种Nm-N = I的感觉,但是不要管它先)
两边转置:
Nm-N = (Nm-N)T Nm-N
转置后,等号右边是一样的,所以,满足:
(Nm-N)T =Nm-N 的Nm- ,就能满足 ||X||²最小。
取:Nm- = NT(NNT)- 能满足 ||X||²最小。
将上式代入: N N-N = N、(N-N)T,都可以得到:
N Nm-N = N、(Nm-N)T=Nm-N
Nm- = NT(NNT)- 的Nm-满足了:
1. 是一个广义逆
2. 能够使得 ||X||²最小。
因为(NNT)- 不唯一,所以Nm- 不唯一,但是其解Y唯一。(只有伪逆N+ 才是唯一的,同时满足4个条件的N- 只有一个!)
但是其解唯一(注意,目前为止,N都是对称矩阵)
证明:任意的 Nm- = NT(NNT)- ,得到的 X =Nm- ATPl 是唯一的。
由于广义逆必须满足:
N = NNm-N
两边转置:
NT = ( NNm-N)T = (Nm-N) TNT, 又 (Nm-N)T =Nm-N 的Nm- ,就能满足 ||X||²最小。
代入得:NT = Nm-NNT
设有两个解:
X1 =Nm1- ATPl
X2 =Nm2- ATPl
那么,对应也有
NT = Nm1-NNT
NT = Nm2-NNT
那么,有:
(Nm1- - Nm2-)NNT = 0,左右两边乘以:(Nm1- - Nm2-),得:
(Nm1- - Nm2-)NNT (Nm1- - Nm2-)T= 0



 浙公网安备 33010602011771号
浙公网安备 33010602011771号