测绘线性代数（三）：伪逆解

原来的说法:

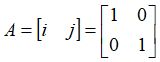
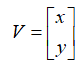
向量V的各个分量，对A的列向量进行线性组合。

V' = x i + y j

 

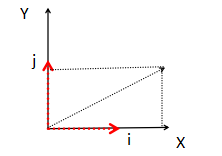
通常，要知道V' 的大小和方向，首先是将i , j 绘制出来，然后用V各个分量对其线性组合。

如果i⊥j ，而且| i | = | j | =1， 如果以 i 和 j 为坐标轴，那么V' 就是V在以i和j为坐标轴下的坐标。

假如，i 和 j 恰好是X轴和Y轴的方向，那么V' = V ， V没有改变(长度，方向都和前后一样)

i和j 将视为坐标系下的一个基

（此处，开始将A看成是作用于V的一个变换，可记为V' =  AV = T(V)）

---

 假如有一个矩阵B，将i变换成i' ，将j变换成 j'  , 那么B对V' 变换为V'' 应该是如何的？

V'' =  BV'  = B(x * i + y * j) =  x B i + yB j  = x i' + y j' = [ i' ,  j' ] V 

为什么说标准正交矩阵如此重要，因为其相当于 i' ⊥ j'  ， | i' | = | j' | =1 , 仅仅对V旋转成V''

B对V'的变换，相对于B先对V的基变换成新的基， 再由V来对新的基线性组合。

---

 

逆矩阵，就是线性变换后的结果V' = AV，然后V = A^-1V' , 将V' 变回V，也就是：V = A^-1AV

但是，A不是什么情况下都有逆。

首先，有线性变换的性质可知，由于A的各列，是V在新坐标系下的各个坐标轴；如果A各列向量长度恰好为1，而且正交，那么将会将V，映射为另一个坐标系下的向量V' , 长度和V一样，方向和V不同。

因此，有两个结论：

1. A要是方阵，因为A^-1 是一个变换还原的问题。

如果A不是方阵，那么有许多AV=A₁V=A₂V=……=V' , 反正从V对A各列线性组合来看，组成V'可以有很多种。

另一个方面，如果A不是方阵，那么V的维数只能“平面” 。

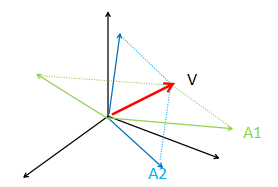
2. A各列必须线性无关。

如果A各列线性相关，那么同样的，有许多AV=A₁V=A₂V=……=V'，从而，将V' 变换回来，有很多A_i^-1  (假如有)

另一个方面，有方程组：

a₁₁ v₁  + a₁₂ v₂ + a₁₃ v₃ = v₁'   (1)

a₂₁ v₁  + a₂₂ v₂ + a₂₃ v₃ = v₂'   (2)

a₃₁ v₁  + a₃₂ v₂ + a₃₃ v₃ = v₃'   (3)

在解这个方程组的时候，传统办法是“高斯消元法”，就是(1)、(2)、(3)式乘以倍数后相减，将原来的AV = V' ，变成 I V = V‘’，那么V就可以解出来，结果V不变。

如果有矩阵[A I]，经过“高斯消元法”，得到[ I E]

如果有：A[I E] = [A I] = [ AI, AE] ，也就是I = AE，E = A^-1   

那么，A必须能够完成整个“高斯消元法”，才能由A变成I 。

要完成消元法，那必须A各行线性独立

对于方阵而言，行线性独立，等价于列线性独立，因为只是坐标系“翻转” 一下而已。

 

---

符合AX=0的所有X，称为A的零空间，又叫：N(A)

假如：A是3x2(mxn)的矩阵，

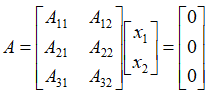
X垂直于A的每个行向量

如果A的2个行向量线性无关，那么A的秩R = 2 ，其行空间的维度也是2，所有X形成的空间，维度是m - R = 1

 

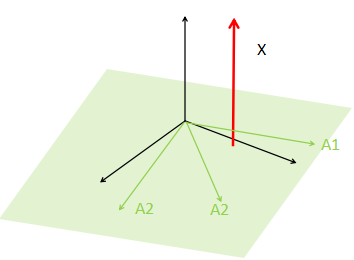
所以，X空间的维度N(A) = m - R

---

 

在前面提及，有情况：

A列向量线性无关，B不在列空间中

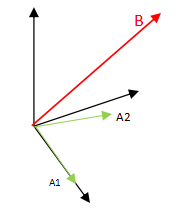
这时，只要Ax=B，左右两边乘以A^T ， 得到A^TAx=A^TB，解此方程，即可获得最小二乘解。

x = (A^TA)^-1 A^TB，A^TA有没有逆矩阵？其答案等价于：A是否“满秩”

假设有A^TAy = C = 0 

那么：y^TC = y^TA^TAy = 0

等价于：||Ay||² = 0

等价于：Ay = 0；

 

所以，对于同一个向量y ， y 垂直于A和 A^TA 的行空间。

所以A和 A^TA 的行空间应该是一样的。行空间的维度(是二维平面还是三维空间) = 秩数

从而，导致R(A) = R(A^TA) = n，也即是A^TA作为nxn矩阵，满秩，固可逆。

---

 但是，通常，我们解A^TAx=A^TB，并不会求(A^TA)^-1 ，因为求逆的代价通常很大的。

如果我们采用上述的“高斯消元法”，将方程组A^TAx=A^TB 理解为，另一个Ax = y 。那么，得到：

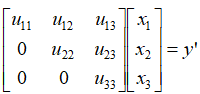
结果，先解出x₃  ，然后回代，解出x₂ ,x₁ 

但是，应该如何记录，“高斯消元法”的各个步骤呢？答案是，左乘一个矩阵。

例如，有矩阵：

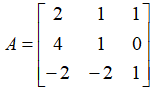
按照“高斯消元法”，第一步，消去第2行第1列的元素。那么，可以左乘一个矩阵E₂₁

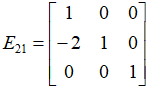
分析E₂₁ ：

第1行表示，1*A的第1行 + 0*A的第2行  + 0*A的第3行 = E₂₁ 的第1行

第2行表示，-2*A的第1行 + 1*A的第2行  + 0*A的第3行 = E₂₁ 的第2行 ， 正好消除了A的第2行第1列的元素

..

假如，A‘ = E₂₁A

那么，最终，U = A''' = E₃₂E₃₁E₂₁A

对于各个E，一定是有逆矩阵的(既然可以将A逐步变成U，那么也可以将U逐步变回A)

所以，A = (E₂₁)^-1(E₃₁)^-1 (E₃₂)^-1U = LU

(由此可见，A需要时满秩矩阵，假如第1行和第2行线性相关，那么乘以E₂₁ ，直接就会将第2行元素全部变成0，导致无法回代了)

上述又叫LU分解，当然，A不止一种分解方式。 OK，矩阵分解的序幕要拉开了。

---

开一下脑洞：

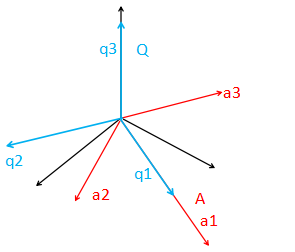
假如有A，有Q，Q的各列向量相互垂直，而且长度都为1，是否可以考虑，有

a₁  = i q₁

a₂ =  j q₁ + k q₂

a₃ = l q₁ + mq₂ + n q₃

也就是

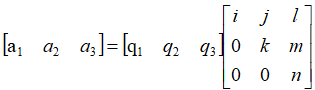
亦即A=QR，又叫QR分解

那R阵，i……n到底是怎么来的呢？Q阵，q₁ ,  q₂  , q₃  是怎么来的？其实很好分析：

(1) q₁  肯定是和a₁同向的，而且长度为1，那么 q1 = a₁ / ||a₁||  ， i = ||a₁||

(2) 由于q₂⊥a₁，那么只要a₂减去在a₁上的分量，得到q₂'，然后q₂=q₂' / ||q₂'|| 即可。

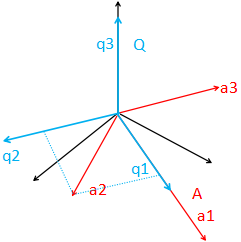
那么，a₂如何减去在a₁上的分量呢？很明显，也就是，q₂' = a₂ - (a₂在a₁上的投影向量)

 一个向量，在另一个向量中的投影如何求？

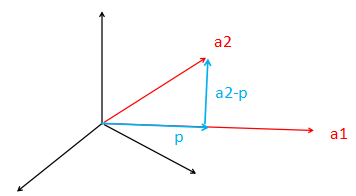
p = x a₁，a₂ - p ⊥ p ，所以  p^T(a₂-p)=0

p^Ta₂ = p^Tp

x a₁^T a₂ = x² a₁^Ta₁

a₁^T a₂ = xa₁^Ta₁，而因为a₁^Ta₁是常数，等于||a₁||²

x = a₁^T a₂ / a₁^Ta₁

所以a₂在a₁的投影公式： 

 

(3) 同理，q3' = a₃ - (a₃在q₁的投影) - (a₃在q₂的投影)

这种办法，又叫Gram-Schmidt正交化过程。

---

 

*由于Q是标准正交方阵，所以Q^TQ=I(对角线就是单位向量的长度平方 =1，非对角线是正交向量的点积=0)，对于列向量无关的最小二乘解：A^TAx=A^Tb，x=(A^TA)^-1A^Tb , 有：

x = (R^TQ^TQR)^-1R^TQ^Tb，从而，x = (R^TR)^-1R^TQ^Tb = R^-1Q^Tb

所以，Rx = Q^Tb  ， 由于R是下三角阵，又可以愉快的回代，直接得出x了。

---

 是时候，要考虑：

A列向量线性相关，而且B也不在A的列空间中

 

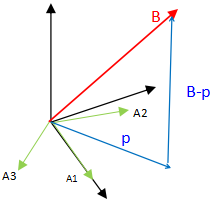
我们的求法，当然是要B投影在A的列空间中，然后找出||X||最小的一组解。

B应该如何投影在列空间中的呢？

 p⊥(B-p) ，所以，p^T(B-p) = 0。有 p = AX（p可以由A各列线性组合得到），所以：

(AX)^TB = (AX)^T(AX)

X^TA^TB=X^TA^TAX

A^TB=A^TAX

又被难住了，当A列线性无关是，A^TA才有逆，p = AX = A (A^TA)^-1A^TB （因此，矩阵P = A (A^TA)^-1A^T 又叫投影矩阵）

那还有什么办法呢？那不找投影了，直接找||X||最小的一组解。

首先，A的行空间 ⊥ A的零空间 (上面已经说明了)，那么，可以说明，X在n维空间中，总可以分解为：X = X在行空间的部分 + X在零空间的部分。

(为了好记住，称X = Xr + Xw)

(1) p = AX = A(Xr + Xw) ，又因为Xw在A的零空间，所以AXw=0，因此：p = AXr，所以Xr可以说是其中一个解。

(2) 那么，X在n维空间中，其Xr分量的长度是固定的，仅有Xw处不同。（这个也不知道如何解析，《线性代数及其应用》P150页提及过）

可能就是：AX=b是一个非齐次线性方程组，对于非齐次线性方程组的通解，就是AXw=0，Xw作为任意解，加上AXr=p作为一个特解；

也就是同解为：X= Xr + Xw，并且Xw是任意的，而Xr是固定的；

当||X||最小，证明X完全在行空间上，自然的Xw=0

（将X最小，转化为求X在行空间的分向量）

 

 

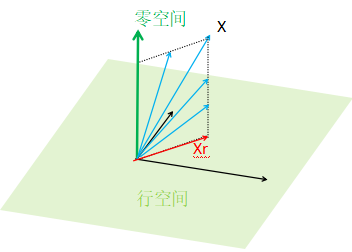
*如果列线性无关的话，可以想象，行空间一定沾满整个Rn；而且X只能在行空间中没法跑，长度固定唯一。

(3) 因此，Xr是最小范数解。

---

 

首先，得知道SVD分解：https://www.cnblogs.com/pylblog/p/10544427.html

X⁺ =  A⁺b

 A⁺ = VΣ⁺ U^T

A⁺ 是A的“伪逆” ，X⁺ 又叫“伪逆解”

因为A⁺ A  =  VΣ⁺ U^T UΣV^T 

而U和V是单位正交矩阵，所以U^TU = I , VV^T  =I 

而ΣΣ⁺ 是对角线为1或0的方阵，所以 A⁺ A 最终也是对角线为1或0的，类似于I的方阵（所以称为“伪”）。

---

那么，剩下只需验证：

一. X⁺ =  A⁺b 是不是符合Xr的特征，也就是X⁺ 是不是在行空间中，从而证明X⁺  的长度是最短的

二 . 前面说过，p = AX = Pb，p是b在A的列空间上的投影

---

 首先，要介绍一种特殊的LU分解：

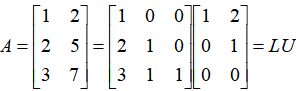
假如，将U的0行去掉，得到：

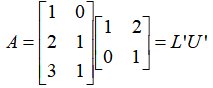
A依然还是A。只是U‘变得可逆了。

A⁺ 又可以表示为：A⁺ = U’^T(U'U'^T)^-1(L'^TL')^-1L'^T  <=>   A⁺ = VΣ⁺ U^T   (注意到此U非彼U)， 因为 A⁺ A  =  A⁺  L'U'  = I 

现在，只要用新的A⁺  来证明前面两个性质:

(1) 令A⁺ = U’^T(U'U'^T)^-1(L'^TL')^-1L'^T   等于 A⁺ = U’^T C

(2) A⁺ b = U’^T Cb  = U’^T y

而U‘ ，更具LU分解的特性，U’ 和 U有着相同的行空间，而U和A又有相同的行空间，所以U'和A有相同的行空间。

而U’^T y  是对 U'^T 列向量的线性组合。换句话说，就是对U' 行向量的线性组合。

结论是，A⁺ b = U’^T y  ，其结果是一个在A的行空间的向量

因此，X⁺ =  A⁺b ，X⁺ 是在行空间中的。

(3) AX⁺   =  AA⁺b = (L'U')(U’^T(U'U'^T)^-1(L'^TL')^-1L'^T  b) = L'(L'^TL')^-1 L'^T b 

而L‘ 和A有相同的列空间，又L'(L'^TL')^-1 L'^T  是一个投影矩阵，因此p = AX⁺ = Pb

验毕！

---

 

应用：

通常在平差中，有观测方程 v = Bx - l ，往往x是近似值X的改正数 ， 最终要获得X’ = X + x

而我们要想 v^T pv最小，就是假想  0 = Bx - l , x有解

从而解方程 B^TpBx = B^Tpl  , 令其为Ax =b

因为没有控制点，或者起算数据，所以造成A秩亏，常规办法，没法得到X‘ 

那么，用伪逆解，可以获得，使得近似值改正数x^Tx 最小，也就是改正数向量x最小的一组解。

换句话说，当近似值是相对坐标（因为没有已知点，或起算数据，只能这样），而且可以从高精度的观测数据推导时，那么解出x的意义是，让这个相对坐标更准确，也就是相互关系更准确！