CT断层成像系列02——Shepp-Logan头模型的平行束投影数据仿真(Matlab|C++代码实现)
时间地点_20260123上海光源
Shepp Logan头的投影数据的数学公式推导
先上一张关键示意图, 来降低理解难度:(就叫他图2.5)
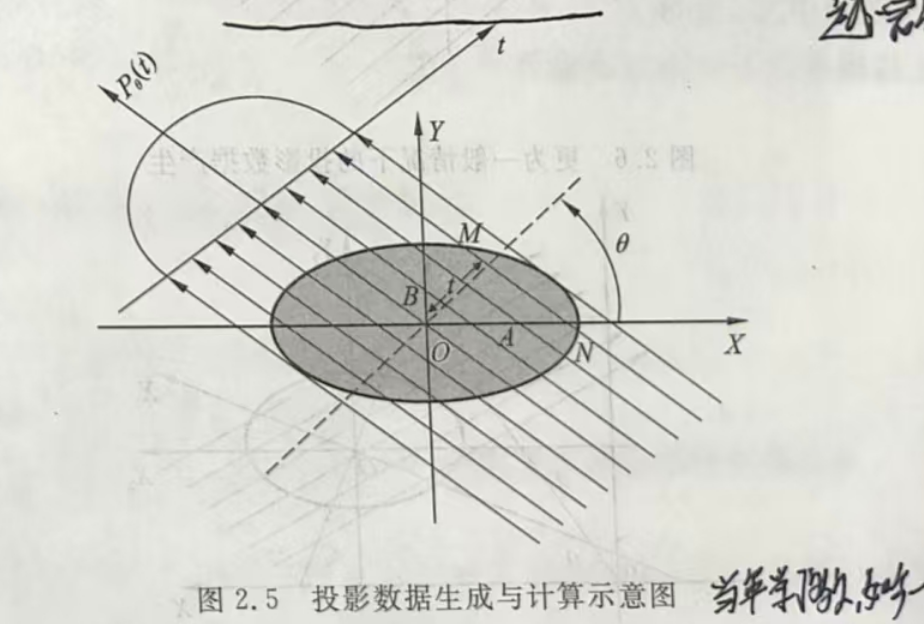
我们假设X射线面阵探测器这一行的像素序列为\(t\), 在\(t\)上的这一层切片的投影数据(灰度值)为\(P_\theta (t)\), 我们与系列01一样先从一个规规整整不旋转且椭圆中心位于中央坐标系原点\(O\)的椭圆来举例. 在CT采集的过程中, 探测器相对于坐标系是旋转的, 这一角度成为\(\theta\) 由于是同步辐射光源出光, X射线束线形状为平行束, 随着距离不会发散, 因此探测器\(t\)距离中央坐标系原点\(O\)的距离无关紧要, 离多远都不会改变投影结果, 探测器距离在讨论中被排除.
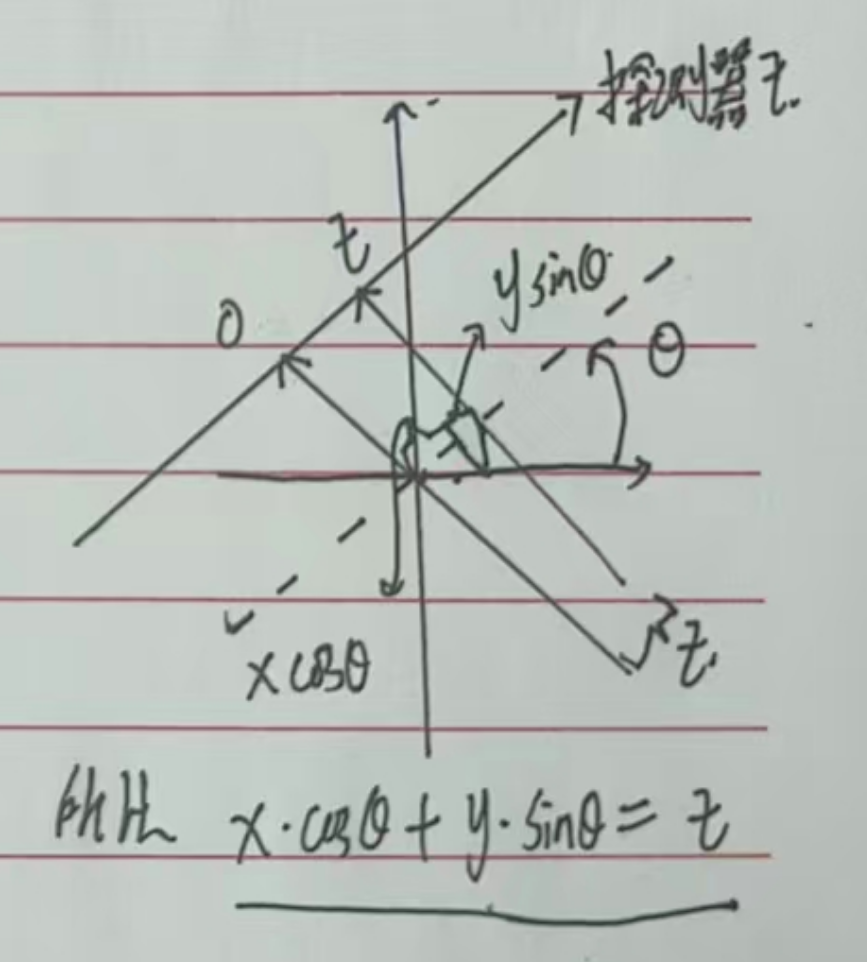
对于探测器任一像素或通道\(t\) (注意,这在算法实现上时常可以是小数), 一束射线先经过样品衰减后到达第\(t\)个像素, 这是它相对于探测器中心位置0的距离. 由我上面的草图可知, 任意打到探测器的射线都可以用\(x\)和\(y\)来表示\(t\):
\[x\cos(\theta)+y\sin(\theta)=t
\]
对于图2.5,里的椭圆, 由系列01我们知道他的表达式为:
\[f(x,y)= \begin{cases} \rho, \quad当\frac{x^2}{A^2}+\frac{y^2}{B^2}\leq 1\\
0, \quad其他
\end{cases}
\]
一束X射线MN打穿椭圆样品射线探测器的第\(t\)个像素上, 射线与椭圆相交于MN两点, 此刻t点的探测器灰度值是射线MN经过样品这一段线段的密度总衰减, 所以探测器像素\(t\) 的灰度为\(P_\theta (t)\):
\[P_\theta (t)=\int_{MN}\rho \,dl = \rho \overline{MN}
\]
\(\rho\)在SL头就是个常数, 所以求投影值就是求MN这一选段的距离. 联立公式(1)(2)(我算到昏厥也没解出来)即可求得射线经过样品的总长度MN为:
\[x_{1,2}=\frac{tA^2\cos\theta\mp AB\sin\theta\sqrt{r^2-t^2}}{r^2}\\
y_{1,2}=\frac{tB^2\sin\theta\pm AB\cos\theta\sqrt{r^2-t^2}}{r^2}\\
\]
在这其中, r为;
\[r^2=A^2\cos^2\theta+B^2\sin^2\theta
\]
那么MN的长度为两点相减, 为"
\[\overline{MN}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\frac{2AB\sqrt{r^2-t^2}}{r^2}
\]
就像前面说的, 有了MN的长度就知道\(P_\theta (t)\)了, 这样, 投影函数\(P_\theta (t)\)的一般表达式为:
\[P_\theta (t)=\begin{cases}\rho\frac{2AB\sqrt{r^2-t^2}}{r^2},\quad 当|t|\leq r\\
\quad\quad0 \quad\quad\ ,\quad \ 当|t|>r
\end{cases}
\]
这样我们就得到了计算规整椭圆的投影数据的数学解析表达式, 下面要融合系列01里随意旋转平移的椭圆得到更泛用的解析解, 由本系列01的公式(5)可知, 一个任意旋转角度任意平移的椭圆在中央坐标系\(XOY\)的表达式为:
\[\frac{((x-x_0)cos\alpha+(y-y_0)sin\alpha)^2}{A^2}+\frac{(-(x-x_0)sin\alpha+(y-y_0)cos\alpha)^2}{B^2}= 1
\]
任意过这个椭圆的射线\(\overline{PQ}\)被椭圆吸收衰减后, 再被探测器的第\(t\)个像素通道所捕获, 该射线的表达式还是:
\[x\cos(\theta)+y\sin(\theta)=t
\]
公式(8)(9)联立即可解得(我解不出来, 抄书了)PQ两点的坐标, 进而得到线段\(\overline{PQ}\)的长度:
\[\overline{PQ}=\frac{2AB\sqrt{r_a^2-d_a^2}}{r_a^2}
\]
在这之中:
\[r_a^2=A^2\cos^2(\theta-\alpha)+B^2\sin^2(\theta-\alpha)\\
d_a=t-x_0\cos\theta-y_0\sin\theta
\]
(11)代入(10), 我们就得到了最终的Shepp-Logan头模型的投影数据的解析解, 投影函数\(P_\theta (t)\)为:
\[\begin{aligned}
P_\theta (t)&=\rho \overline{PQ}\\
&=\rho \frac{2AB\sqrt{A^2\cos^2(\theta-\alpha)+B^2\sin^2(\theta-\alpha)-(t-x_0\cos\theta-y_0\sin\theta)^2}}{A^2\cos^2(\theta-\alpha)+B^2\sin^2(\theta-\alpha)}
\end{aligned}
\]
其中\(\rho、A、B、\alpha、\theta和\alpha\)分别是椭圆密度、长半轴、短半轴、旋转角和探测器旋转角。 对于S-L头模型，我们逐角度的，把每个椭圆的投影累加就得到了投影数据。 至此， 由系列01和02我把S-L头的所有知识讲完了。
Shepp Logan头的投影数据的代码实现
Matlab|直接调用Radon（拉东）函数实现SL头投影数据：
化身调包侠， 光速拿下：
clc;clear all;close all;
I=phantom(256);%生成256*256的Shepp Logan头模型
theta=0:179;%投影角度
P=radon(I,theta);%生成投影数据
figure;imshow(I,[]),title('256*256头模型图像');
figure;imagesc(P),colormap(gray),colorbar,title('180°平行束投影图像');
运行结果：
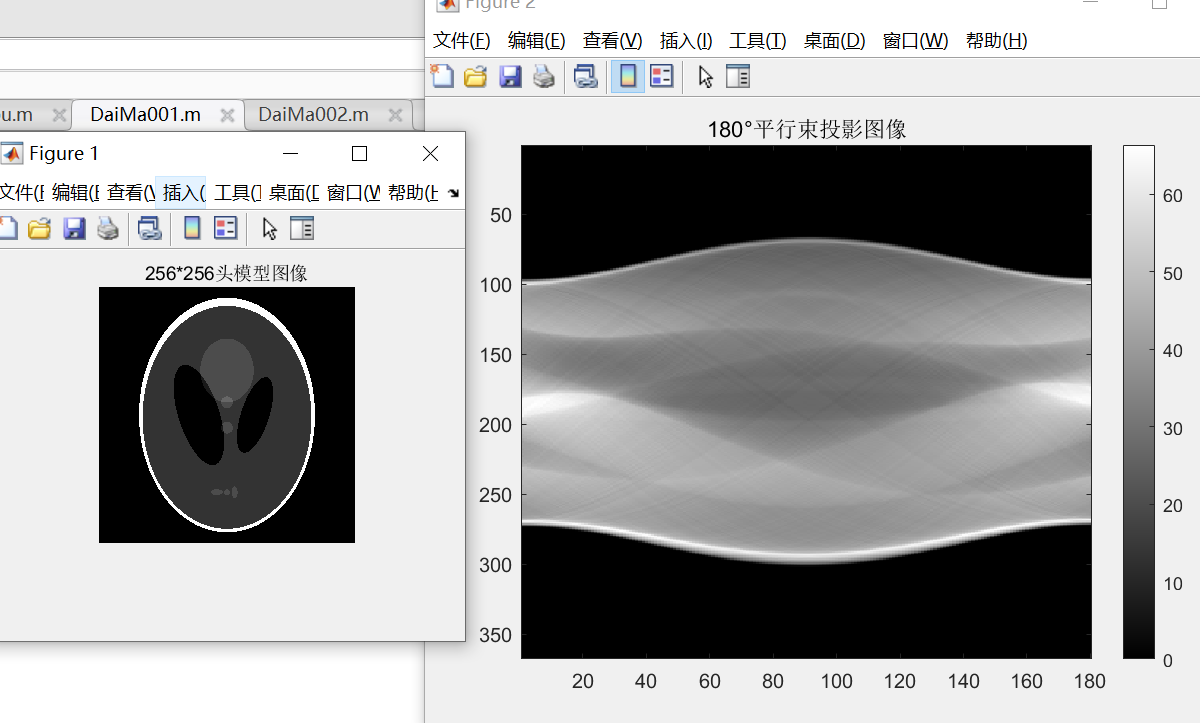
拉东法很泛用，啥图都能生成投影数据， 系列03讲它。
Matlab|利用数学解析法手搓SL头投影数据：
利用公式（12）手搓轮子， 数学解析的实现SL头投影数据：
clc;clear all;close all;
%%======仿真参数设置======%%
N=256;%重建图像大小,探测器通道个数
theta=0:1:179;%投影角度
%%======产生仿真数据======%%
I=phantom(N); %生产Shepp_Logan头模型
N_d=2*ceil(norm(size(I)-floor((size(I)-1)/2)-1))+3; %设定探测器通道|像素个数
P=medfuncParallelBeamForwardProjection(theta,N,N_d); %产生投影数据
%%======仿真结果显示======%%
figure;imshow(I,[]),title('256*256头模型图像'); %显示原始图像
figure;imagesc(P),colormap(gray),colorbar,title('180°平行束投影图像'); %显示投影数据
function P=medfuncParallelBeamForwardProjection(theta,N,N_d)
%Parallel beam forward projection function
%-----------
%输入参数
%theta:探测器的旋转角度|投影角度矢量 indegrees
%N 图像大小;N_d 探测器通道个数|一行的像素数
%-----------
%输出参数
%P:投影数据矩阵(N_d*theta_num) 也就是我们平时实验得到的数据Projection
%%========================================%%
%椭圆绘图的六个参数 A密度|振幅 a长轴 b短轴 x0椭圆心横坐标 y0椭圆形纵坐标 α旋转角度
shep=[
1 .69 .92 0 0 0
-.8 .6624 .8740 0 -.0184 0
-.2 .1100 .3100 .22 0 -18
-.2 .1600 .4100 -.22 0 18
.1 .2100 .2500 0 .35 0
.1 .0460 .0460 0 .1 0
.1 .0460 .0460 0 -.1 0
.1 .0460 .0230 -.08 -.605 0
.1 .0230 .0230 0 -.606 0
.1 .0230 .0460 .06 -.605 0
];
theta_num=length(theta);
P=zeros(N_d,theta_num);%存放投影数据
rho=shep(:,1).';%椭圆对应密度
%参数是百分数,乘N椭圆扩张到整个图像
ae=0.5*N*shep(:,2)';%椭圆长半轴
be=0.5*N*shep(:,3).';%椭圆短半轴
xe=0.5*N*shep(:,4).';%椭圆中心x坐标
ye=0.5*N*shep(:,5).';%椭圆中心y坐标
alpha=shep(:,6).';%椭圆旋转角度
alpha=alpha*pi/180;%角度变弧度
theta=theta*pi/180;
TT=-(N_d-1)/2:(N_d-1)/2;%探测器像素们的序列号|探测器坐标
for k1=1:theta_num
P_theta=zeros(1,N_d);%存放每一角度投影数据
for k2=1:max(size(xe))
a= (ae(k2)*cos(theta(k1)-alpha(k2)))^2+(be(k2)*sin(theta(k1)-alpha(k2)))^2;
%整个公式串就只有TT是矩阵,其他都是常数,所以这里之后是点乘点除.Matlab可以不用逐个像素for循环,而是以矩阵直接运算
%这样做极大减少心智负担,但是性能堪忧算的太慢,
temp=a-(TT-xe(k2)*cos(theta(k1))-ye(k2)*sin(theta(k1))).^2;
ind = temp>0;%根号内值需为非负
P_theta(ind)=P_theta(ind)+rho(k2)*(2*ae(k2)*be(k2)*sqrt(temp(ind)))./a;
end
P(:,k1)=P_theta.';
end
end
运行结果如下：
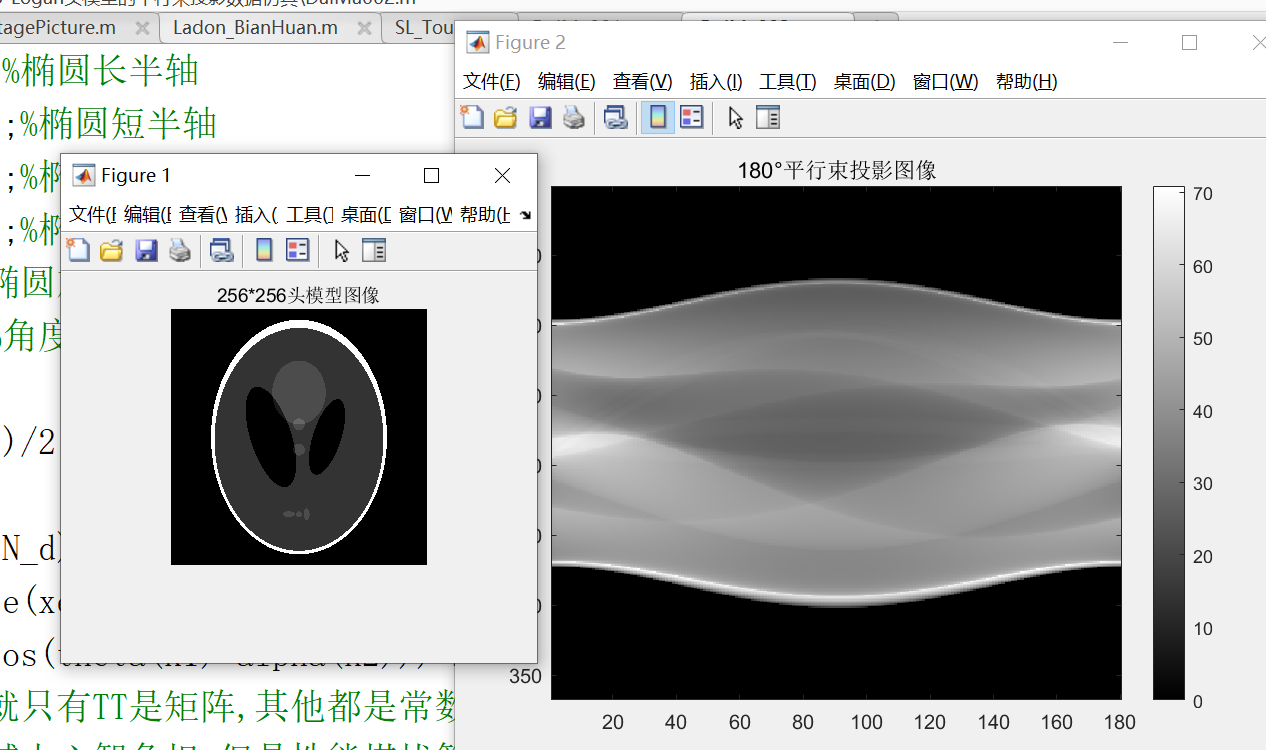
C++|利用数学解析法手搓SL头投影数据：
还是那句话， Matlab也好Python也好， 这些人类友好语言都太慢太慢了， 动辄算几个小时， 这是没法落地的。据我观察， 工业届医疗届的高性能程序或者图像密集型程序都是C++写的。当然还有更底层更快的，用嵌入式或FPGA，扯远了， 附上C++实现的代码：
// main.cpp
// g++ main.cpp -std=c++11 `pkg-config --cflags --libs opencv4` -o slphantom
#include <opencv2/opencv.hpp>
#include <vector>
#include <cmath>
const double PI = 3.14159265358979323846;
// ---------- 1. 生成 Shepp-Logan 头模型 ----------
cv::Mat phantom(int N)
{
// 11 个椭圆的参数：密度 长轴 短轴 中心x 中心y 旋转角(度)
const double shep[11][6] = {
{1.0, 0.69, 0.92, 0.0, 0.0, 0.0},
{-0.8, 0.6624,0.874, 0.0, -0.0184,0.0},
{-0.2, 0.11, 0.31, 0.22, 0.0, -18.0},
{-0.2, 0.16, 0.41, -0.22, 0.0, 18.0},
{0.1, 0.21, 0.25, 0.0, 0.35, 0.0},
{0.1, 0.046, 0.046, 0.0, 0.1, 0.0},
{0.1, 0.046, 0.046, 0.0, -0.1, 0.0},
{0.1, 0.046, 0.023,-0.08, -0.605, 0.0},
{0.1, 0.023, 0.023, 0.0, -0.606, 0.0},
{0.1, 0.023, 0.046, 0.06, -0.605, 0.0}
};
cv::Mat img = cv::Mat::zeros(N, N, CV_64F);
double cx = (N - 1) * 0.5, cy = cx;
for (int y = 0; y < N; ++y)
{
double yy = y - cy;
for (int x = 0; x < N; ++x)
{
double xx = x - cx;
double val = 0.0;
for (int k = 0; k < 10; ++k)
{
double rho = shep[k][0];
double a = shep[k][1] * N * 0.5;
double b = shep[k][2] * N * 0.5;
double x0 = shep[k][3] * N * 0.5;
double y0 = shep[k][4] * N * 0.5;
double alpha = shep[k][5] * PI / 180.0;
double x1 = (xx - x0) * cos(alpha) + (yy - y0) * sin(alpha);
double y1 = -(xx - x0) * sin(alpha) + (yy - y0) * cos(alpha);
double r2 = (x1 * x1) / (a * a) + (y1 * y1) / (b * b);
if (r2 <= 1.0) val += rho;
}
img.at<double>(y, x) = val;
}
}
cv::Mat out;
cv::normalize(img, out, 0, 255, cv::NORM_MINMAX, CV_8U);
return out;
}
// ---------- 2. 平行束前向投影 ----------
cv::Mat medfuncParallelBeamForwardProjection(const std::vector<double>& thetaDeg,
int N, int N_d)
{
// 同样 10 个椭圆参数（只取前 10 个，和 MATLAB 一致）
const double shep[10][6] = {
{1.0, 0.69, 0.92, 0.0, 0.0, 0.0},
{-0.8, 0.6624,0.874, 0.0, -0.0184,0.0},
{-0.2, 0.11, 0.31, 0.22, 0.0, -18.0},
{-0.2, 0.16, 0.41, -0.22, 0.0, 18.0},
{0.1, 0.21, 0.25, 0.0, 0.35, 0.0},
{0.1, 0.046, 0.046, 0.0, 0.1, 0.0},
{0.1, 0.046, 0.046, 0.0, -0.1, 0.0},
{0.1, 0.046, 0.023,-0.08, -0.605, 0.0},
{0.1, 0.023, 0.023, 0.0, -0.606, 0.0},
{0.1, 0.023, 0.046, 0.06, -0.605, 0.0}
};
int nAng = thetaDeg.size();
cv::Mat P = cv::Mat::zeros(N_d, nAng, CV_64F); // 投影矩阵
// 把椭圆参数一次性换算到像素坐标
std::vector<double> rho(10), ae(10), be(10), xe(10), ye(10), alpha(10);
for (int k = 0; k < 10; ++k)
{
rho[k] = shep[k][0];
ae[k] = shep[k][1] * N * 0.5;
be[k] = shep[k][2] * N * 0.5;
xe[k] = shep[k][3] * N * 0.5;
ye[k] = shep[k][4] * N * 0.5;
alpha[k] = shep[k][5] * PI / 180.0;
}
// 探测器坐标 [-range ... +range]
std::vector<double> TT(N_d);
for (int i = 0; i < N_d; ++i) TT[i] = i - (N_d - 1) * 0.5;
for (int k1 = 0; k1 < nAng; ++k1)
{
double th = thetaDeg[k1] * PI / 180.0;
std::vector<double> P_theta(N_d, 0.0);
for (int k2 = 0; k2 < 10; ++k2)
{
double ca = cos(th - alpha[k2]);
double sa = sin(th - alpha[k2]);
double a = ae[k2] * ae[k2] * ca * ca + be[k2] * be[k2] * sa * sa;
double xc = xe[k2] * cos(th) + ye[k2] * sin(th);
for (int i = 0; i < N_d; ++i)
{
double t = TT[i] - xc;
double tmp = a - t * t;
if (tmp > 0)
{
double len = 2.0 * ae[k2] * be[k2] * sqrt(tmp) / a;
P_theta[i] += rho[k2] * len;
}
}
}
// 写回列向量
for (int i = 0; i < N_d; ++i)
P.at<double>(i, k1) = P_theta[i];
}
return P;
}
// ---------- 3. 主函数 ----------
int main()
{
const int N = 256;
const int N_d = 2 * static_cast<int>(
std::ceil(std::sqrt(2.0) * (N - 1) * 0.5)) + 3;
std::vector<double> thetaDeg;
for (int i = 0; i < 180; ++i) thetaDeg.push_back(i); // 0~179°
// 1. 生成头模型
cv::Mat I = phantom(N);
// 2. 前向投影
cv::Mat P = medfuncParallelBeamForwardProjection(thetaDeg, N, N_d);
// 3. 显示
cv::imshow("256×256 Shepp-Logan", I); // 缩放到 0~1 方便显示
cv::Mat P_show;
cv::normalize(P, P_show, 0, 1, cv::NORM_MINMAX);
cv::imshow("180° Parallel-beam sinogram", P_show);
cv::waitKey(0);
// 4. 可选：写盘
//cv::imwrite("phantom.png", I * 255);
// cv::imwrite("sinogram.png", P_show * 255);
return 0;
}
运行结果如下:
结束, 系列03介绍更通用的投影数据获得方法——拉东函数正向投影， 进而还能引出拉东反向投影，也就是CT重建算法FBP了
浙公网安备 33010602011771号