Coursera概率图模型(Probabilistic Graphical Models)第四周编程作业分析
Decision Making
作决策
这一周的内容在老版本的CS228课程中,是作为第六周的一个小节讲的(老版本的CS229只有9周的课程),而在概率图模型的教材里边对应的是第22章效用和决策。也就是说,这一周的课程更多的是对之前所学知识的一种应用。
1.记号和定义
使用影响图来表现本周所学的内容,如下图所示:
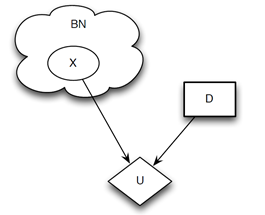
其中,X表示随机变量,D表示决策节点,U表示效用节点。
2.已知决策规则的期望效用
我们可以将随机变量与决策节点一起看做一个贝叶斯网络,并只保留效用节点的父节点,即对其它节点用VariableElimination函数进行变量消除,将所得因子的val值与效用节点的val值相乘即可。公式如下式所示:
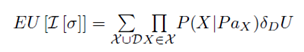
SimpleCalcExpectedUtility.m 简单计算期望效用
参考代码如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % % YOUR CODE HERE % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% V = unique([F(:).var]); Z = setdiff(V, U.var); Fnew = VariableElimination(F, Z); Ffinal = Fnew(1); for ii = 2 : length(Fnew) Ffinal = FactorProduct(Ffinal, Fnew(ii)); end Ffinal.val = Ffinal.val / sum(Ffinal.val); U_reorder_val = zeros(size(U.val)); for ii = 1 : prod(U.card) U_reorder_val(ii) = GetValueOfAssignment(U, IndexToAssignment(ii, U.card), Ffinal.var); end EU = Ffinal.val * U_reorder_val';
2.基于期望效用因子最大化期望效用
上一章的公式可以变形如下式:
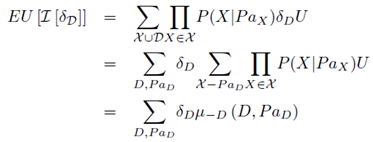
我们需要计算的期望效用,就是式中的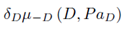 部分。这里我们可以将随机变量与效用节点一起看做一个贝叶斯网络,将网络中与决策节点无关的变量消除,其剩余因子的因子积就是我们要求的最大期望效用。
部分。这里我们可以将随机变量与效用节点一起看做一个贝叶斯网络,将网络中与决策节点无关的变量消除,其剩余因子的因子积就是我们要求的最大期望效用。
CalculateExpectedUtilityFactor.m 计算期望效用因子
参考代码如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % % YOUR CODE HERE... % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% F = [I.RandomFactors, I.UtilityFactors]; V = unique([F(:).var]); Z = setdiff(V, I.DecisionFactors(1).var); Fnew = VariableElimination(F, Z); EUF = Fnew(1); for ii = 2 : length(Fnew) EUF = FactorProduct(EUF, Fnew(ii)); end
OptimizeMEU.m 优化最大期望效用
这里就是取效用最大的决策方案。注意一下多个决策节点时OptimalDecisionRule.var的含义。
参考代码如下:
OptimalDecisionRule = CalculateExpectedUtilityFactor(I); if length(OptimalDecisionRule.var) == 1 [MEU, index] = max(OptimalDecisionRule.val); OptimalDecisionRule.val = zeros(size(OptimalDecisionRule.val)); OptimalDecisionRule.val(index) = 1; else assignments = IndexToAssignment(1 : prod(OptimalDecisionRule.card(1 : end - 1)), OptimalDecisionRule.card(1 : end - 1)); MEU = 0; for ii = 1 : OptimalDecisionRule.card(end) indices1 = AssignmentToIndex([assignments, ii * ones(size(assignments, 1), 1)], OptimalDecisionRule.card); [meu, indices2] = max(OptimalDecisionRule.val(indices1)); MEU = MEU + meu; OptimalDecisionRule.val(indices1) = 0; OptimalDecisionRule.val(indices1(indices2)) = 1; end end
3.多效用因子
我们还往往会遇到不止一个效用节点的情况,如下图所示:
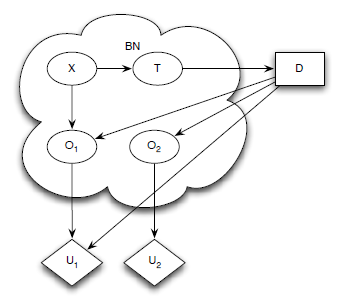
这种情况下,我们当然是选择能够使多个效用节点期望值的和最大的决策啦。我们有两种处理方案:一种是直接求出每一个效用节点的期望值,之后直接加和即可;另一种是利用下式所示的公式对效用节点进行变形,之后直接计算最大期望效用即可。
上述的两种方法都会要用到因子求和函数,这个函数在这一周的作业中并没有提供……但是,可以在第七周的作业PA-Exact-Inference-Release中找到,函数名为FactorSum.m,直接把函数的全部内容复制在我们这一周的作业后边就好。
FactorSum.m 因子求和
第七周作业提供的代码如下:
function C = FactorSum(A, B) if (isempty(A.var)), C = B; return; end; if (isempty(B.var)), C = A; return; end; [dummy iA iB] = intersect(A.var, B.var); if ~isempty(dummy) assert(all(A.card(iA) == B.card(iB)), 'Dimensionality mismatch in factors'); end C.var = union(A.var, B.var); [dummy, mapA] = ismember(A.var, C.var); [dummy, mapB] = ismember(B.var, C.var); C.card = zeros(1, length(C.var)); C.card(mapA) = A.card; C.card(mapB) = B.card; C.val = zeros(1,prod(C.card)); assignments = IndexToAssignment(1:prod(C.card), C.card); indxA = AssignmentToIndex(assignments(:, mapA), A.card); indxB = AssignmentToIndex(assignments(:, mapB), B.card); C.val = A.val(indxA) + B.val(indxB); end
OptimizeWithJointUtility.m 联合效用优化
参考代码如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % % YOUR CODE HERE % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% U = I.UtilityFactors(1); for ii = 2 : length(I.UtilityFactors) U = FactorSum(U, I.UtilityFactors(ii)); end I.UtilityFactors = U; [MEU, OptimalDecisionRule] = OptimizeMEU(I);
OptimizeLinearExpectations.m 线性期望优化
参考代码如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % % YOUR CODE HERE % % A decision rule for D assigns, for each joint assignment to D's parents, % probability 1 to the best option from the EUF for that joint assignment % to D's parents, and 0 otherwise. Note that when D has no parents, it is % a degenerate case we can handle separately for convenience. % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% OptimalDecisionRule = struct('var', [], 'card', [], 'val', []); for ii = 1 : length(I.UtilityFactors) I_ = I; I_.UtilityFactors = I.UtilityFactors(ii); EUF_ = CalculateExpectedUtilityFactor(I_); OptimalDecisionRule = FactorSum(OptimalDecisionRule, EUF_); end if length(OptimalDecisionRule.var) == 1 [MEU, index] = max(OptimalDecisionRule.val); OptimalDecisionRule.val = zeros(size(OptimalDecisionRule.val)); OptimalDecisionRule.val(index) = 1; else assignments = IndexToAssignment(1 : prod(OptimalDecisionRule.card(1 : end - 1)), OptimalDecisionRule.card(1 : end - 1)); MEU = 0; for ii = 1 : OptimalDecisionRule.card(end) indices1 = AssignmentToIndex([assignments, ii * ones(size(assignments, 1), 1)], OptimalDecisionRule.card); [meu, indices2] = max(OptimalDecisionRule.val(indices1)); MEU = MEU + meu; OptimalDecisionRule.val(indices1) = 0; OptimalDecisionRule.val(indices1(indices2)) = 1; end end
交作业的截图:
这两周诸事繁杂,所以概率图的学习进度放缓了些,下周开始要保持正常进度才行……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号