[CG learning] shading

== Diffuse Shading ==

​ 🔥 对表面颜色的控制

​ 🌲 diffuse reflection，漫反射

• Lambertian Shading Model

  现实中大多数物件表面都是非光滑的（"matte"）

  

  lambertian surface 👉 朗伯表面就是理想情况的漫反射表面，不考虑观察角度的影响

  A Lambertian surface for reflection is a surface that appears uniformly bright from all directions of view and reflects the entire incident light. Lambertian reflectance is the property exhibited by an ideal matte or diffusely reflecting surface.

  https://www.azooptics.com/Article.aspx?ArticleID=790

  • Lambert's cosine law

    基本定义：物体表面某点的颜色正比于其法向量与光照向量形成角度\(\theta\)​的余弦值\(cos\theta\)​ 👇

    \(c \propto |cos\theta|\)​ 用向量形式可以表达为 👉 \(1. \space c \propto max(0, \vec n·\vec l) \\ 2. \space c \propto |\vec n·\vec l|\)​

  • 影响因素

    • diffuse reflectance \(c_r\) ⚠️ 根据颜色不同反射率也不同
    • light intensity \(c_l\)​​​ 光照强度引起的颜色值变化，规范化到range[0,1]

  • 基本形式 \(1. \space c \propto c_rc_lmax(0, \vec n·\vec l) \\ 2. \space c \propto c_rc_l|\vec n·\vec l|\)

    • \(cos_\theta\) 小于0时理论上应该没有颜色，但是代入等式\((2)\)得到存在颜色，因此\((2)\)描述的是一个两侧对称光照的情况

• Ambient Shading

  \(c \propto max(0,\vec n·\vec l)\) 中存在一个明显的问题，背光处均为黑色，但在实际中光到处反射，使得背光处不可能为完全的黑色。

  因此等式中还需要加入环境光\(c_a\)​ 👉 \(c\propto c_r(c_a+c_lmax(0, \vec n·\vec l))\)​

  🌲 由于RGB range \([0,1]^3\) ，可能需要进行clamp处理

• Vertex-Based Diffuse Shading

  • avoid faceted appearance

    

    https://www.gia.edu/gems-gemology/optimizing-face-up-appearance-in-colored-gemstone-faceting

  以triangle表面的法线向量（normal vector）来计算颜色值时，得到的颜色值会用于填充整个三角形面的每一个像素点，相邻两个三角形面如果颜色差异明显，会出现faceted appearence的问题。

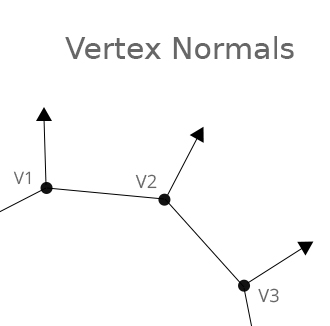
  因此考虑将法线向量放到三角形的顶点上，计算出三角形各顶点的颜色值，再通过插值法得到整个三角形各像素点的颜色 👉 simpest way: just average the normals of triangles which shared that vertice.

  

  

  http://benchung.com/basic-glsl-displacement-shader-three-js/

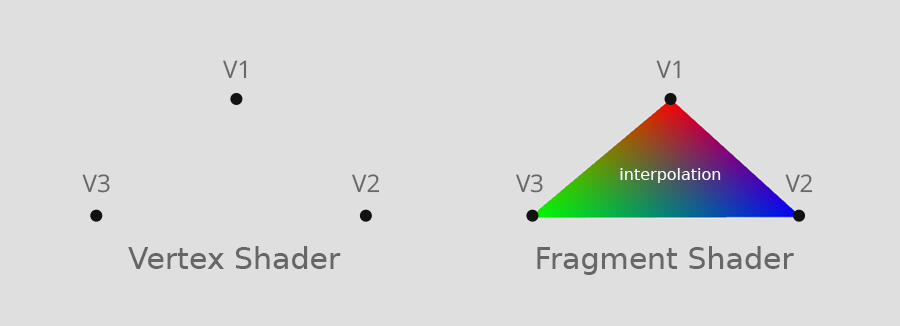
  • Surface Normal Vector Interpolation
    interpolate vertex color and normal using barycentric coordinates

    \[\alpha = \frac{S_{cap}}{S_{abc}}\\ \beta = \frac{S_{abp}}{S_{abc}} \\ \theta = \frac{S_{bcp}}{S_{abc}} \]

    • vertex color 👉 \(c = \alpha c_0 + \beta c_1 + \gamma c_2\)
    • vertex normal 👉 \(c = \alpha \vec c_0 + \beta \vec n_1 + \gamma \vec c_2\)

== Phong Shading ==

​ 🔥 对高光颜色的控制

​ matte surface也会有highlights存在，且高光并非是以表面材料的颜色为主，从材料表面反射的散射光对整体颜色影响不大

• Phong Lighting Model

  

  https://www.geertarien.com/blog/2017/08/30/blinn-phong-shading-using-webgl/

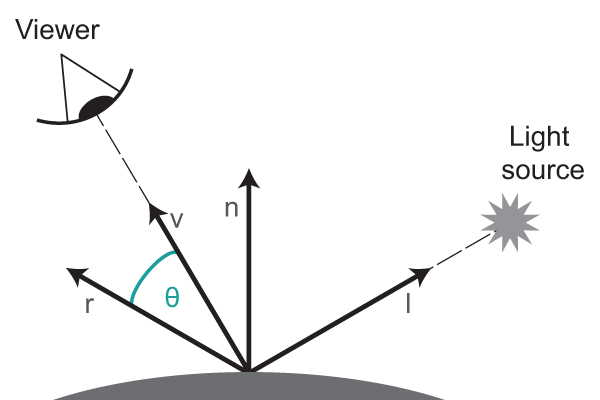
  当视线与反射光的夹角\(\theta\)​​ 小于一定值时，我们就会看到高光

  可以得到等式 \(c = c_l(\vec v·\vec r)\)​​

  ​ 🌲v stands for view；当\(v = r\)时，反射光与视线重合，\(\vec v·\vec r = 1\) 👉 \(c = c_l\)​

  • \(s\)​​​ Phong exponent

    \(c = c_l(max(0,\vec v·\vec r))^s\)​​​​​​​

    🌲 s stands for specular，鉴于\(\vec v·\vec r\)得到的\(cos\theta\)值range[0,1]，更大的Phong指数，会使得高光越小

    The s term in the equation represents the roughness of the surface. A smooth surface, which should have a smaller highlight, has a large s. Since the cosine of the angle is a number on [0, 1], taking it to a power greater than 1.0 will make the number smaller. Therefore, a large s exponent will make for a small highlight.

    https://paroj.github.io/gltut/Illumination/Tut11 Phong Model.html

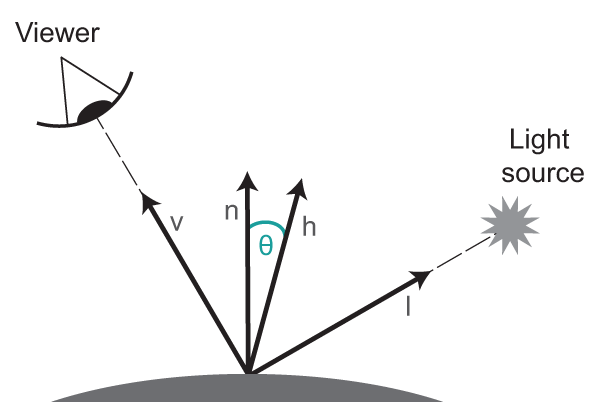
  • halfway vector 表达的等式

    \(c = c_l(\vec h·\vec n)^s\)​

    • \(\vec h = \frac{\vec v + \vec l}{||\vec v + \vec l||}\)​​

      🌲 highlights appear when \(\vec h\) is near \(\vec n\)

      

      https://www.geertarien.com/blog/2017/08/30/blinn-phong-shading-using-webgl/

      🌲 \(\theta_{new} = \frac{\theta_{old}}{2}\)，因此此处的\(s\) 也能和\(c = c_l(max(0,\vec v·\vec r))^s\)的\(s\)有相同的控制效果

  • 实际使用中通常将Lambertian shading model和Phong Lighting Model中的两个等式结合在一起

    \[c = c_r(c_a + c_l max(0, \vec n · \vec l)) + c_l(\vec h · \vec n)^p \]

  • 再加入新的控制变量\(c_p\)用于控制高光的颜色

    \[c = c_r(c_a + c_l max(0, \vec n · \vec l)) + c_lc_p(\vec h · \vec n)^p \]

== ☕️ ==

• Fundamentals of Computer Graphics, Fourth Edition - Marschner Steve, Shirely Peter

• https://developer.valvesoftware.com/wiki/Phong_materials

• https://paroj.github.io/gltut/Illumination/Tut11 Phong Model.html

• https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-rendering-a-triangle/barycentric-coordinates