梯度下降算法(SGD, Momentum, NAG, Adagrad, RMProp, Adam)及其收敛效果比较，优化器

从一批次所用数据量的角度可以分为：全量梯度下降(batch GD)，小批量梯度下降(mini-batch GD)，随机梯度下降(SGD，一次只用一个样本计算梯度并更新参数)。batch GD, mini-batch GD, SGD都可以看成SGD的范畴，只不过区别在于每次取多少的样本了。

从梯度的更新公式的角度可以分为：SGD, SGD with momentum, NAG (Nesterov Accelerated Gradient), AdaGrad, AdaDelta, RMSProp, Adam, Nadam。这些优化算法的区别在于是否用到了一阶动量（历史梯度的指数移动评价）、二阶动量（历史梯度平方的指数移动平均）、是否是自适应的。$\sigma$

1. 梯度下降

沿着目标函数梯度的反方向搜索极小值。

式中，$\theta$是模型参数，$J(\theta)$目标函数（损失函数），$\eta$是学习率。

2. 小批量随机梯度下降（mini-batch SGD）

每次随机选定一小批(mini-batch)数据进行梯度的计算，而不是计算全部的梯度。所有小批量数据都训练完，我们称为完成了一个迭代期(epoch)。

3. SGD with Momentum

想象损失函数是一个山谷，一个球从山谷滑下来，在一个平坦的地势，球的滑动速度会慢下来，可能会陷入一些鞍点或局部最小值，如下图(左)所示。这时候给它增加动量就可以让高处滑落的势能转化为平地滚动的动能，相当于利用惯性增加了小球在平地滑动的速度，从而帮助其跳出鞍点或局部极小点。怎么计算动量呢？动量的计算基于前面的梯度，也就是参数更新不仅基于当前的梯度，也基于之前的梯度，如下图(右)所示。

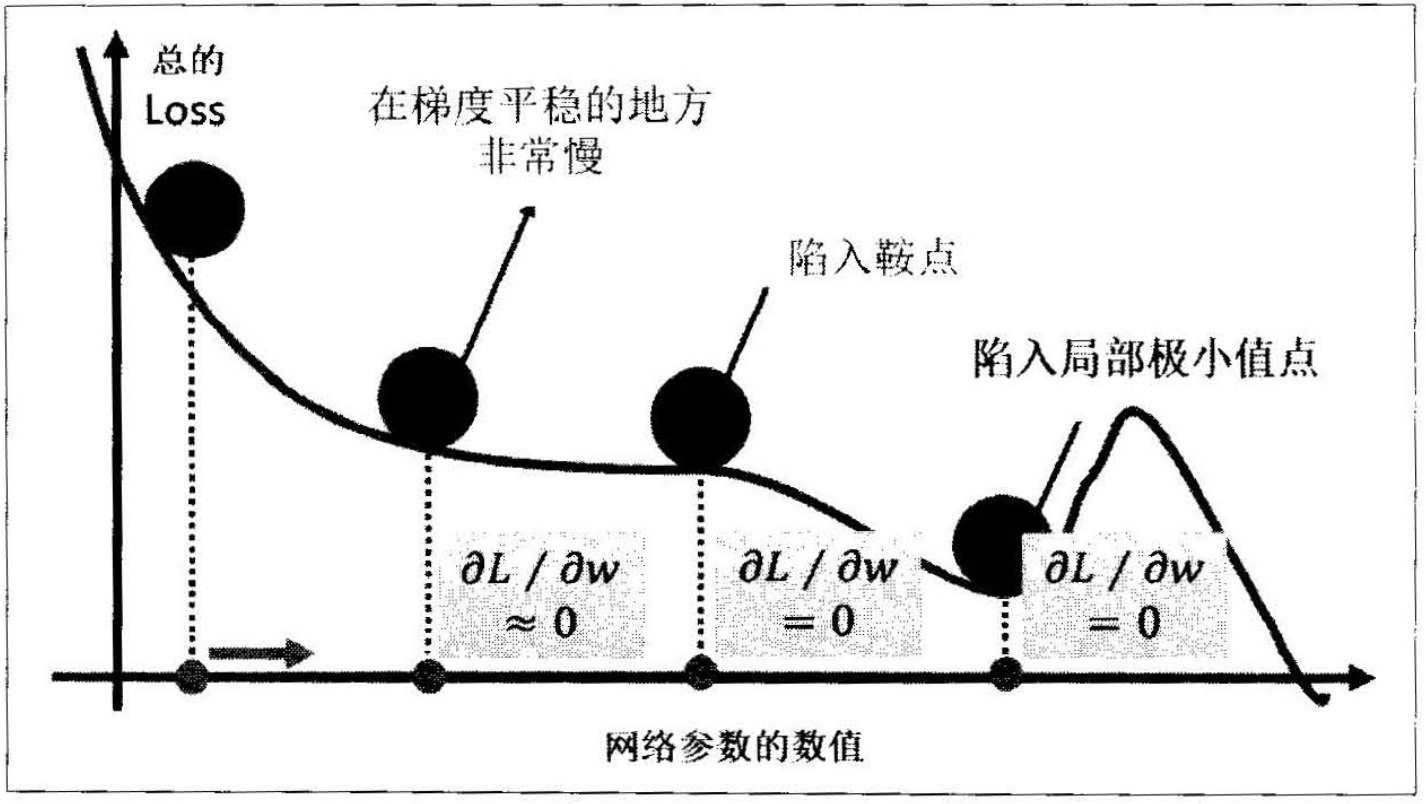
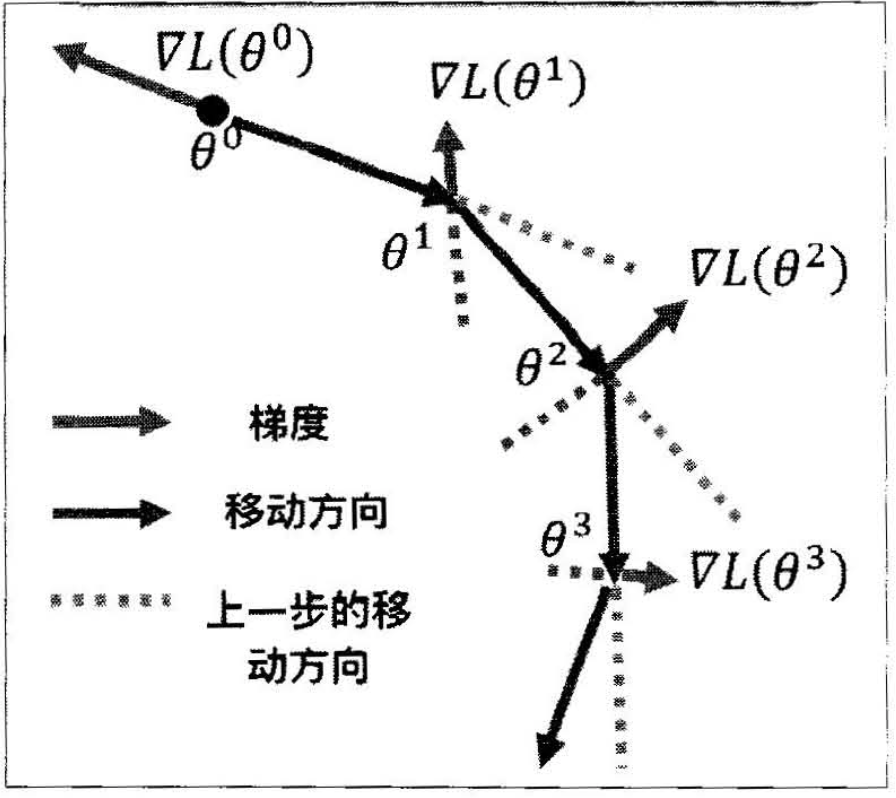
(a) 增加动量 (b) 动量的计算

模型参数更新公式：

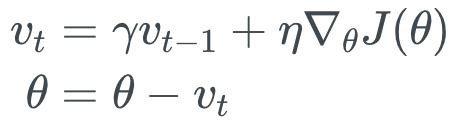
Momentum梯度下降方法在搜索极小值时，若不发生震荡，则加动量可起到加速收敛的效果；若发生震荡，则加动量可起到减少震荡的效果，因为前一次的梯度和当前的梯度的方向是想反的。具体可参考这篇博客。

即，Momentum可以加速收敛，抑制震荡。

4. Nesterov accelerated gradient (NAG)

NAG方法和momentum方法相似。momentum方法计算的是当前位置的梯度，NAG方法计算的是经过更新之后的位置的梯度，其参数更新公式为

经过变换之后的等效形式中，NAG算法相对于Momentum多了一个本次梯度相对上次梯度的变化量，这个变化量本质上是对目标函数二阶导的近似。由于利用了二阶导的信息，NAG算法才会比Momentum具有更快的收敛速度。

5. Adagrad （Adaptive Gradient，自适应梯度）

上文提到的梯度下降方法中，模型所有的参数在每次更新时使用的是相同的学习率，在Adagrad算法中，每个参数的学习率各不相同。计算某参数的学习率时需将该参数前面所有时间步的梯度平方求和，随着时间步的增加，学习率将减小。

式中，$\theta_{t,i}$表示第$t$时间步的第$i$个参数，$g_{t,i}$表示第$t$时间步的第$i$个参数的梯度。Adgrad方法中，学习率一直在衰减，所以可以起到抑制震荡的作用，一个简单的例子可以参考这篇文章。对于频繁更新的参数，它们的二阶动量比较大，学习率小；对于不怎么更新的参数，它们的二阶动量比较小，学习率就大。但因为那个分母是单调递增的，会使得学习率单调递减至0，可能会使得训练过程提前结束，即便后续还有数据也无法学到必要的知识。

6. AdaDelta / RMProp

Adagrad方法的学习率有时衰减得太快了，AdaDelta / RMProp用指数移动平均值改善了这个问题。

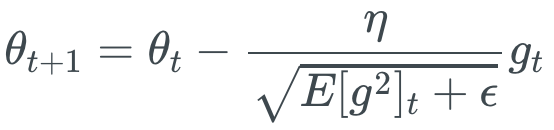
式中，$\gamma$常设置为0.9，$\theta$常设置为0.001。

越靠前面的梯度，对学习率的影响越小，这样可以避免学习率过快衰减。

7. Adam

SGD with momentum在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是Adam了——Adaptive + Momentum。

Adam的权重参数最终更新方程是：

$ \theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{\tilde{V}_t}+\epsilon} \tilde{m}_t $

Adam的优点：不太需要过多的调参技巧，类似于傻瓜相机，用就完了。

Adam的缺点：可能不收敛；可能错过全局最优解；占用一定的内存空间；可能破坏其它正则化的理论要求环境。

8. Nadam

8. 各方法收敛效果比较^[3]

代码：

import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

LR = 0.01
BATCH_SIZE = 32
EPOCH = 12

# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))

# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()

# put dateset into torch dataset
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)


# default network
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(1, 20)   # hidden layer
        self.predict = torch.nn.Linear(20, 1)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

if __name__ == '__main__':
    # different nets
    net_SGD         = Net()
    net_Momentum    = Net()
    net_RMSprop     = Net()
    net_Adam        = Net()
    nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]

    # different optimizers
    opt_SGD         = torch.optim.SGD(net_SGD.parameters(), lr=LR)
    opt_Momentum    = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
    opt_RMSprop     = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
    opt_Adam        = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
    optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]

    loss_func = torch.nn.MSELoss()
    losses_his = [[], [], [], []]   # record loss

    # training
    for epoch in range(EPOCH):
        print('Epoch: ', epoch)
        for step, (b_x, b_y) in enumerate(loader):          # for each training step
            for net, opt, l_his in zip(nets, optimizers, losses_his):
                output = net(b_x)              # get output for every net
                loss = loss_func(output, b_y)  # compute loss for every net
                opt.zero_grad()                # clear gradients for next train
                loss.backward()                # backpropagation, compute gradients
                opt.step()                     # apply gradients
                l_his.append(loss.data.numpy())     # loss recoder

    labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
    for i, l_his in enumerate(losses_his):
        plt.plot(l_his, label=labels[i])
    plt.legend(loc='best')
    plt.xlabel('Steps')
    plt.ylabel('Loss')
    plt.ylim((0, 0.2))
    plt.show()

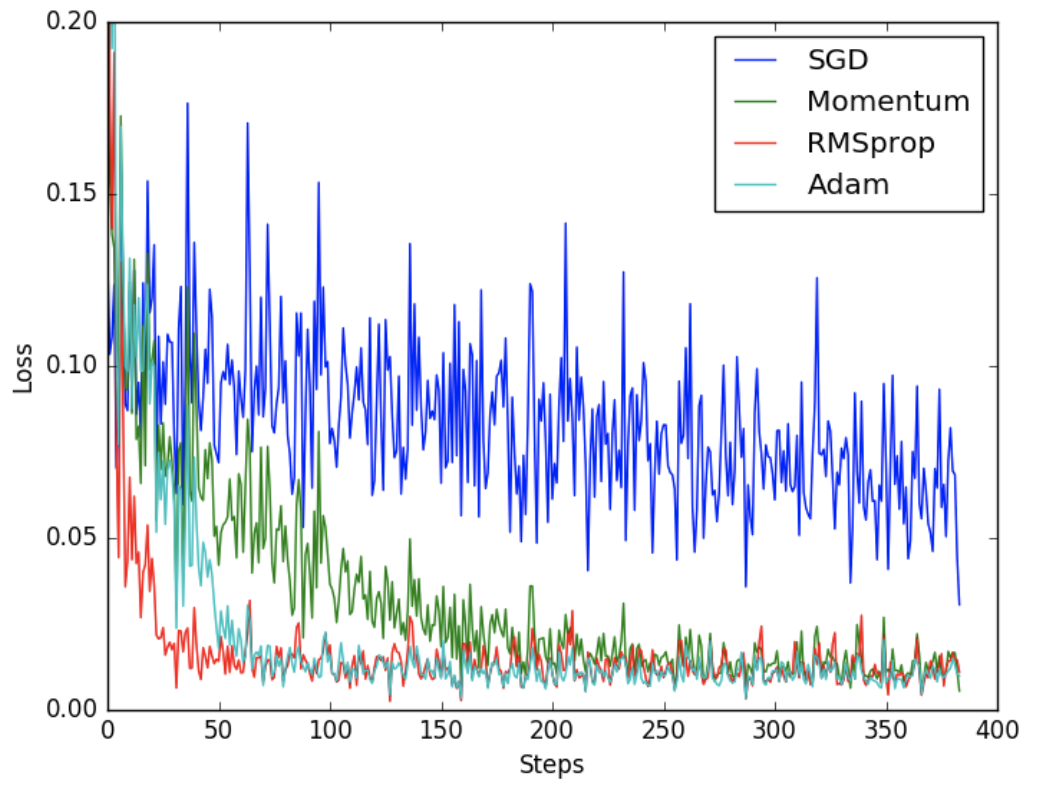
收敛效果比较：