强化学习中的重要概念
Action Space(行为空间)
定义:在所在环境中所有有效的行为的集合叫行为空间。
一些环境是有离散的行为,对于agent来说是有限的行为,如Atari游戏、Alpha Go。
其他的环境是有连续的行为,如在真实世界的机器人的控制角度等。
Policy(策略)
定义:策略是一种被agent使用去决定采取什么行为的规则。
若该policy是确定性的,通常用μ记为:
若该policy是随机性的,通常用记为:
Trajectories(轨迹)/episodes /rollouts
一个轨迹是真实世界中一系列的状态行为:
状态转移可以是确定性的:
状态转移可以是随机性的:
Reward and Return(奖励和返回)
奖励函数R是基于当前的状态、采取的行为和下一个状态:。也常被简化为只依赖于当前状态
或状态行为对
.
第一类返回是有限范围的返回R:
第二类返回是无限范围的返回R:
Value Fuction(值函数)
1.on-policy值函数 :,时间是有限范围时:
,时间是无限范围时:
2.on-policy行为值函数:
3.最优值函数:
4.最优行为值函数:
on-policy值函数和on-policy行为值函数关系:
解释:因为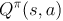 是每采取一个
是每采取一个策略采样得到的a所得的奖励值,若根据一个
策略采样a执行获得奖励直到程序终止所累积的奖励值期望即为
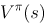
最优值函数和最优行为值函数的关系:
解释:因为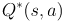 是执行行为a之后所有Q值中的最大值,也就是V的最大值
是执行行为a之后所有Q值中的最大值,也就是V的最大值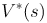
说明:Q值是某状态执行某行为之后获得累计奖励的期望,V值是某状态下可以总共获得累计奖励的期望。V值包含Q值。
Bellman equation(贝尔曼方程)
以上所有四个值函数遵守特别的一致性的方程叫作贝尔曼方程。
贝尔曼方程的基本思想:你当前状态的价值是你希望从该状态得到的奖励加上你下一次到达的状态的值。
对于on-policy值函数的贝尔曼方程是:
其中, 是
的缩写,表示下一次状态
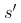 是从环境的转移规则上采样得到;
是从环境的转移规则上采样得到; 是
的缩写;
是
的缩写
对于最优值函数的贝尔曼方程是:
在on-policy值函数的贝尔曼方程和最优值函数之间关键的区别是在行为上是否可得到最大值的奖励。
Advantage Fuction(优势函数)
优势函数 相当于一个策略
,描述的是在状态s下采取一个确切动作a有多好。
数学上,优势函数的定义是
Markov Decision Processes (MDPs)
一个马尔可夫决策过程是一个五元组
是使用有效状态的集合
是所有有效行为的集合
是带有
的奖励函数
是带有在当前状态
采取行为
转换到状态
的概率
的转换概率函数
-
起始状态分布.(类似折扣因子γ)
损失函数(Loss)
作用:判断是否奖励处于稳定值,是否收敛。
如下公式,若此次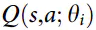 和上一次
和上一次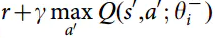 相差不大,则趋于稳定。r是采取当前行为a后获取的奖励,γ是衰减因子,取0~1之间的数。
相差不大,则趋于稳定。r是采取当前行为a后获取的奖励,γ是衰减因子,取0~1之间的数。
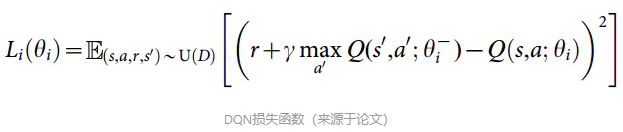




 浙公网安备 33010602011771号
浙公网安备 33010602011771号