数值优化
Steepest Gradient Descent:
- constant step size : \(\tau = c\) 固定梯度大小
- Diminishing step size: \(\tau = c/k\) 每次迭代后,梯度都减小
- Exact line search \(\tau = \arg \mathop{\min}\limits_{\alpha} f(x^{k} + \alpha d)\)
- Inexact line search \(\tau \in { \alpha | f(x^{k}) - f(x^{k} + \alpha d) \geq -c \cdot \alpha d^{T} \bigtriangledown f(x^{k}) }\)
Inexact line search:
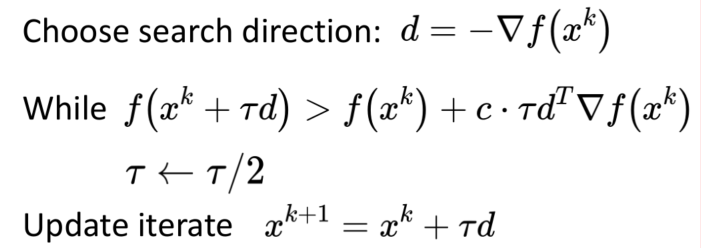
Newton's Method:
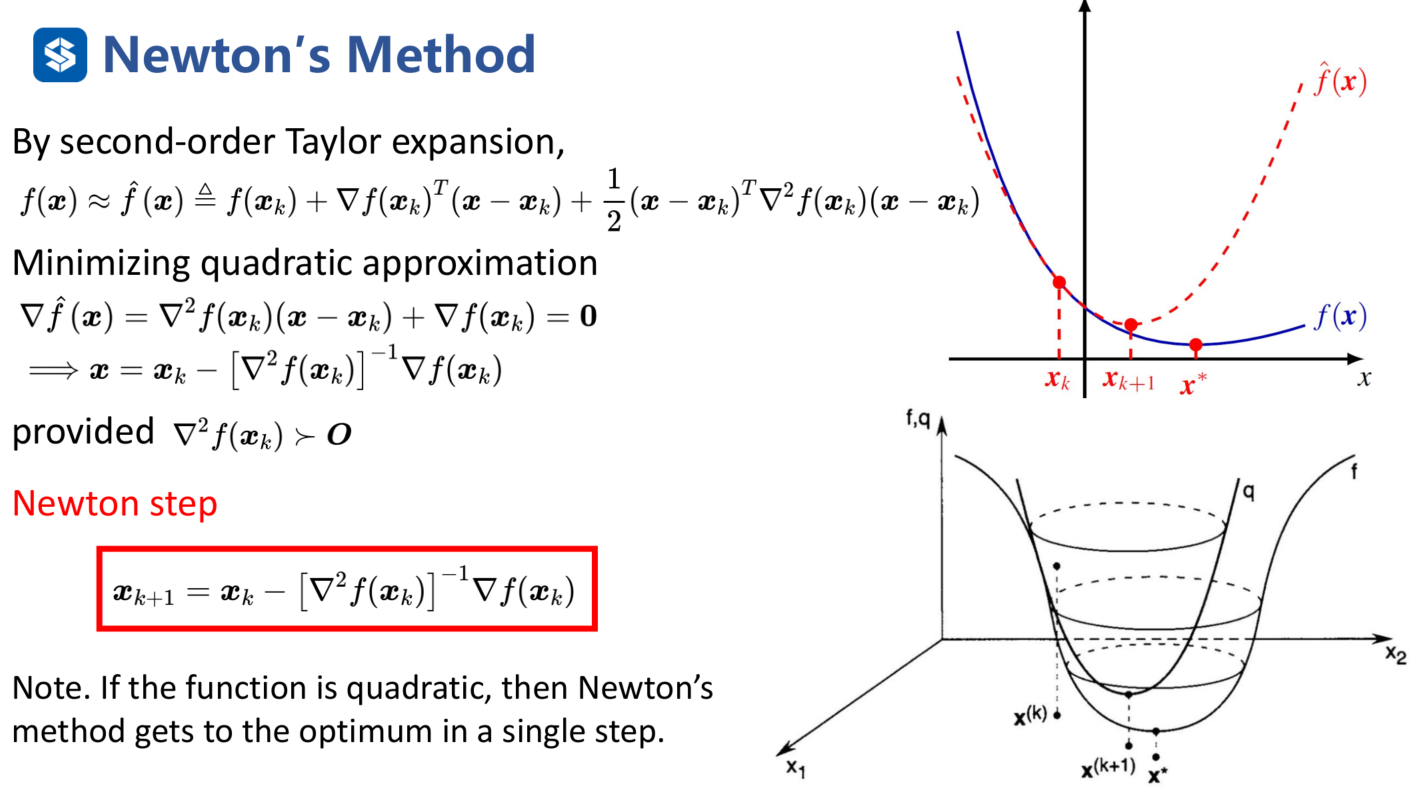
用泰勒展开到Hessian矩阵,这是一个二次型函数,最低点位置就是下次迭代的点。

问题:
- 需要计算Hessian的逆
- Hessian一定是正定的,如果是半正定的,会有奇异值是有零的,没法求逆。如果是不定的,那有可能会往增大的方向迭代
- 原函数、一阶导和二阶导都要是连续的
Practical Newton's Method:修正阻尼牛顿法,为了解决牛顿法非凸函数的不稳定性

- 寻找一个严格正定的M,去接近Hessian矩阵
- 求d的时候,可以用dM = f(x),线性求解出d。
- 不需要求解Hessian矩阵
怎么求M:
- 如果函数是凸的:
- 那Hessian一定是正定的。选择 M = Hessian + 很小的I矩阵
- \([\bigtriangledown ^{2} f(x)]d = - \bigtriangledown f(x)\)
- \(Md = - \bigtriangledown f(x), M = LL^{T}\), 用Cholesky分解将M分解为上三角和下三角的形式,可以很快的将d求解出来
- 如果函数是非凸的,那么Hessian是不定的:
- \(Md = - \bigtriangledown f(x), M = LBL^{T}\) B是一个对角矩阵
- B可以由b1,b2,b3...构成; b可能由一个常数(正的)或\(R^{2*2}\)的矩阵,这个矩阵一定有2个特征值,一正一负。
- Bunch-Kaufman Factorization
Quasi Newton's Method:拟牛顿法,BFGS,省去Hession逆矩阵求解,仍然需要函数是凸的,而且是光滑的
- BFGS相比较牛顿收敛次数会多一点,但是计算复杂度会下降很多
思路依然是找一个M矩阵去贴近Hession矩阵
\(\triangle x = x^{k+1} - x^{k}\)
\(\triangle g = \bigtriangledown f(x^{k+1}) - \bigtriangledown f (x^{k})\)
构建公式:
\(\triangle g \approx M^{k+1} \triangle x\)
\(\triangle x \approx B^{k+1} \triangle g, M^{K+1} B^{k+1} = I\)
怎么挑选B



对于非凸但平滑的BFGS优化算法:
- 只要保证\(\triangle g^{T} \triangle x > 0; B^{0}=I\)是正定的,那么后续\(B^{k+1}\)就一定是正定的
怎么保证\(\triangle g^{T} \triangle x > 0\): Wolfe conditions
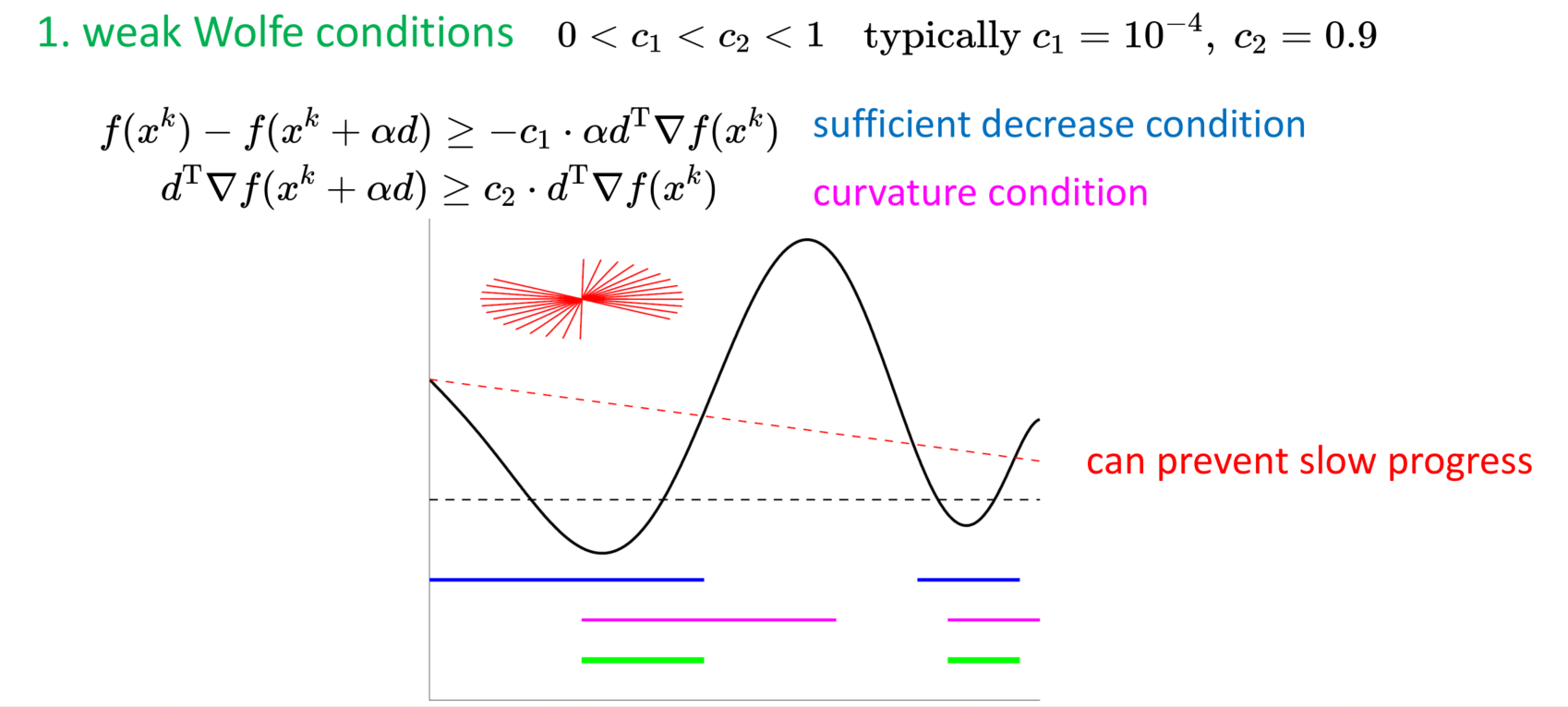
strong Wolfe conditions:

BFGS无法保证一定能够收敛到梯度为0的地方,但是也仅限于一些特定的函数的迭代初期,如果后面已经到局部的时候,BFGS基本可以到达最优点
为了防止这种现象,当然也可以加一个条件 Li and Fukushima。工程上面大多数可以不用


上面的方案在拟合\(B^{k}\)的时候,会用上所有的\(\triangle g 和 \triangle x\),如果迭代的比较远的时候,历史的信息反而会产生干扰,而且B的矩阵也会变稠密
- 采用一个滑动窗口的形式保留\(\triangle g 和 \triangle x\)


