长链剖分学习笔记

一、长链剖分概述

温馨提示：在阅读本文之前，请确保你会重链剖分。

我们知道，每次选一个 sz 最大的子节点作为重儿子，就是重链剖分。

换一种决策重儿子的方式，每次选一个 mxd （走到叶节点经过点数）最大的点作为重儿子，就是长链剖分。

void dfs1(int u,int _f)
{
    mxd[u]=1;///mxd存储路径上点数而不是边数,叶节点mxd=1
    for(auto v:g[u])
    {
        if(v==_f) continue;
        dfs1(v,u);
        mxd[u]=max(mxd[u],mxd[v]+1);
        if(mxd[v]>=mxd[son[u]]) v=son[u];
    }
}

长链剖分的性质：

• 任意一个点的 \(k\) 级祖先所在长链长度 \(\ge k\) 。

• 从任意一个点到根，至多经过 \(\sqrt{2n}\) 条长链。

  最坏情况下每跳一步都能切换一条长链。

  对于 fa[u] ，因为 u 是轻儿子，所以它至少有一条长为 \(1\) 的链。

  对于 fa[fa[u]] ，因为 fa[u] 是轻儿子，所以它至少有一条长为 \(2\) 的链。

  依次类推，假设 \(u\) 到根经过了 \(m\) 条长链，那么至少有 \(1+2+\cdots+m\le n\) 个点，因此 \(m\le\sqrt{2n}\) 。

二、树上 \(k\) 级祖先

这是长链剖分的一个经典应用，直接上模板题。

例1、\(\texttt{P5903 【模板】树上 K 级祖先}\)

题目描述

给定一棵 \(n\) 个点的有根树， \(q\) 次询问 \(u\) 的 \(k\) 级祖先，强制在线。

数据范围

• \(2\le n\le 5\cdot 10^5,1\le q\le 5\cdot 10^6\) 。
• \(0\le k\lt d_u\) 。

时间限制 \(\texttt{3s}\) ，空间限制 \(\texttt{500MB}\) 。

分析

正好借这个题梳理一下求树上 \(k\) 级祖先的常见做法。

离线 dfs

都离线了还需要做？

用栈维护尚未回溯的节点，\(\texttt{dfs}\) 到 \(u\) 时回答询问。

时间复杂度 \(\mathcal O(n)-\mathcal O(1)\) 。

倍增

预处理 f[u][i] 表示 \(u\) 的 \(2^i\) 级祖先，回答时将 \(k\) 二进制分解即可。

时间复杂度 \(\mathcal O(n\log n)-\mathcal O(\log n)\) 。

#include<bits/stdc++.h>
#define ui unsigned int
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<23,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int maxn=5e5+5;
ui n,q,r,s;
long long res;
vector<int> g[maxn];
int d[maxn],fa[maxn][19];
char buf[1<<23],*p1=buf,*p2=buf,obuf[1<<23],*O=obuf;
ui read()
{
    ui q=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) q=10*q+ch-'0',ch=getchar();
    return q;
}
ui get(ui &s)
{
    return s^=s<<13,s^=s>>17,s^=s<<5,s;
}
void dfs(int u)
{
    for(auto v:g[u])
    {
        d[v]=d[u]+1,fa[v][0]=u;
        for(int i=1;i<=18;i++) fa[v][i]=fa[fa[v][i-1]][i-1];
        dfs(v);
    }
}
int query(int u,int k)
{
    for(int i=__lg(k);i>=0;i--) if(k>>i&1) u=fa[u][i];
    return u;
}
int main()
{
    n=read(),q=read(),s=read();
    for(int i=1;i<=n;i++)
    {
        int x=read();
        if(x) g[x].push_back(i);
        else r=i;
    }
    d[r]=1,dfs(r);
    for(int i=1,now=0;i<=q;i++)
    {
        int u=(get(s)^now)%n+1,k=(get(s)^now)%d[u];
        res^=1ll*i*(now=query(u,k));
    }
    printf("%lld\n",res);
    return 0;
}

树链剖分

如果 \(u\) 到重链链顶距离 \(\gt k\) ，暴力往上跳；否则由于重链上的点 \(\texttt{dfs}\) 序连续，可以直接得到答案。

时间复杂度 \(\mathcal O(n\log n)-\mathcal (\log n)\) 。

#include<bits/stdc++.h>
#define ui unsigned int
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<23,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int maxn=5e5+5;
ui n,q,r,s,cnt;
long long res;
vector<int> g[maxn];
int d[maxn],fa[maxn],sz[maxn],son[maxn];
int id[maxn],dfn[maxn],top[maxn];
char buf[1<<23],*p1=buf,*p2=buf,obuf[1<<23],*O=obuf;
ui read()
{
    ui q=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) q=10*q+ch-'0',ch=getchar();
    return q;
}
ui get(ui &s)
{
    return s^=s<<13,s^=s>>17,s^=s<<5,s;
}
void dfs1(int u)
{
    sz[u]=1;
    for(auto v:g[u])
    {
        d[v]=d[u]+1,fa[v]=u,dfs1(v),sz[u]+=sz[v];
        if(sz[v]>=sz[son[u]]) son[u]=v;
    }
}
void dfs2(int u,int _f)
{
    dfn[u]=++cnt,id[cnt]=u,top[u]=_f;
    if(son[u]) dfs2(son[u],_f);
    for(auto v:g[u]) if(v!=son[u]) dfs2(v,v);
}
int query(int u,int k)
{
    k=d[u]-k;
    while(d[top[u]]>k) u=fa[top[u]];
    return id[dfn[u]-d[u]+k];
}
int main()
{
    n=read(),q=read(),s=read();
    for(int i=1;i<=n;i++)
    {
        int x=read();
        if(x) g[x].push_back(i);
        else r=i;
    }
    d[r]=1,dfs1(r),dfs2(r,r);
    for(int i=1,now=0;i<=q;i++)
    {
        int u=(get(s)^now)%n+1,k=(get(s)^now)%d[u];
        res^=1ll*i*(now=query(u,k));
    }
    printf("%lld\n",res);
    return 0;
}

长链剖分

具体步骤如下：

• 找到 \(k\) 二进制下最高位的 \(1\) ，记为 \(h\) 。（\(2^h\le k<2^{h+1}\)）
• 记 \(u\) 的 \(2^h\) 级祖先为 \(x\) 。那么 \(u\) 的 \(k\) 级祖先就是 \(x\) 的 \(k-2^h\) 级祖先，令 \(u\gets x,h\gets h-2^k\) 。此后 \(u\) 到 \(k\) 级祖先的距离一定小于 \(u\) 到长链链底的距离。
• 记 y=top[x],l=d[x]-d[y] ，对 \(k\) 和 \(l\) 的大小关系分类讨论。

若 \(k\le l\) ，如下图：

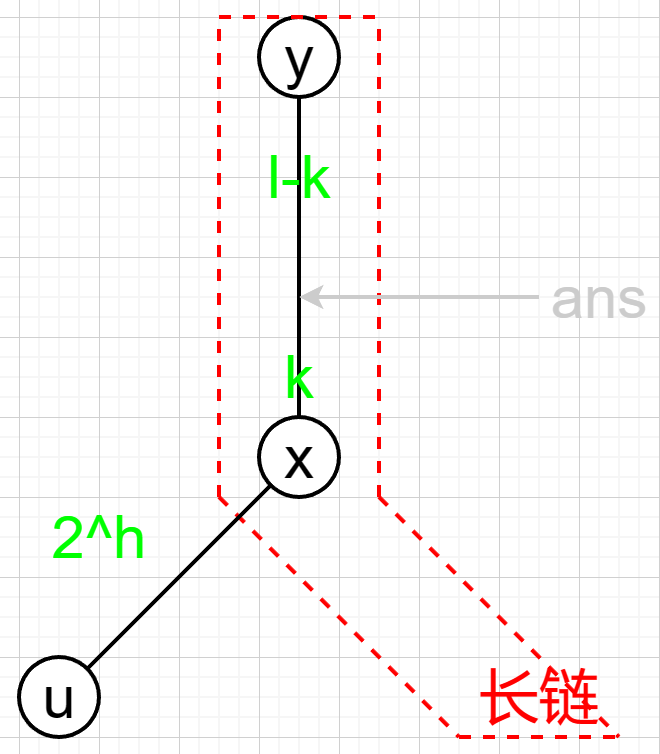
求 \(x\) 的 \(k\) 级祖先，等价于求链上 \(y\) 的 \(l-k\) 级后继。

预处理数组 dn ，对 \(\forall\) 链顶 \(u\) 和 \(k\lt mxd_u\)， dn[dfn[u]+k] 表示链上 \(u\) 的 \(k\) 级后继。

这种情况答案为 dn[dfn[y]+l-k] 。

若 \(k\gt l\) ，如下图：

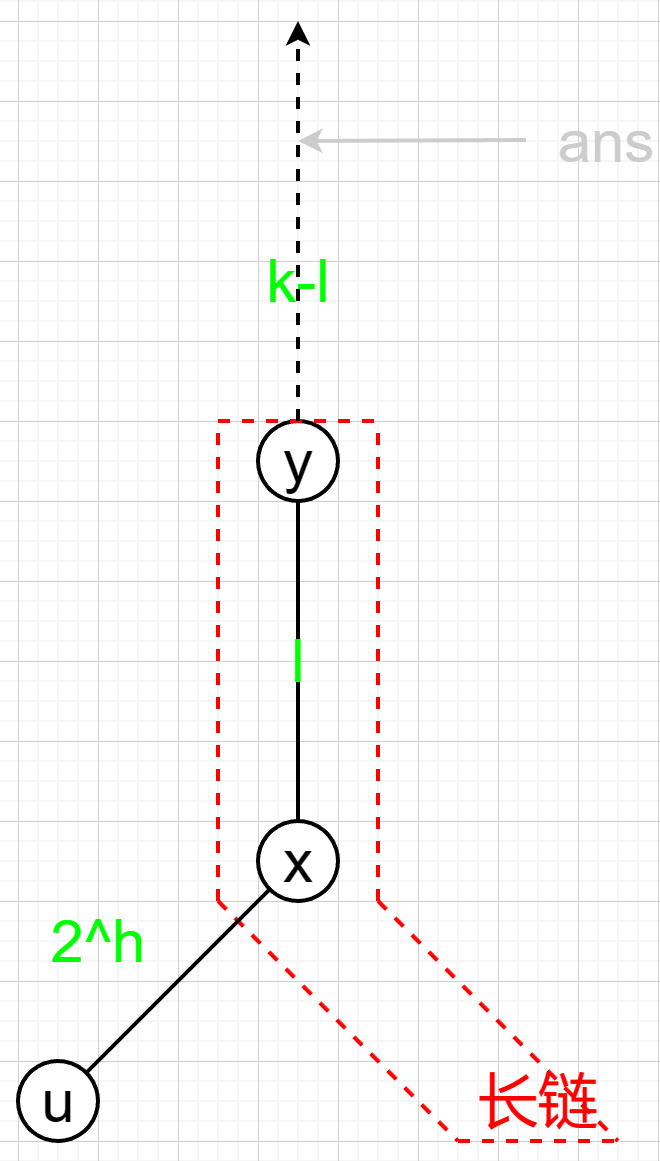
求 \(x\) 的 \(k\) 级祖先，等价于求 \(y\) 的 \(k-l\) 级祖先。

预处理数组 up ，对 \(\forall\) 链顶 \(u\) 和\(k\lt mxd_u\)， up[dfn[u]+k] 表示 \(u\) 的 \(k\) 级祖先。

这种情况答案为 up[dfn[y]+k-l] 。

---

记得不要忘了特判 \(k=0\) 的情况。

时间复杂度 \(\mathcal O(n\log n)-\mathcal O(1)\) 。

#include<bits/stdc++.h>
#define ui unsigned int
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<23,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int maxn=5e5+5;
ui n,q,r,s,cnt;
long long res;
vector<int> g[maxn];
int d[maxn],fa[maxn][19],mxd[maxn],son[maxn];
int dn[maxn],up[maxn],dfn[maxn],top[maxn];
char buf[1<<23],*p1=buf,*p2=buf,obuf[1<<23],*O=obuf;
ui read()
{
    ui q=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) q=10*q+ch-'0',ch=getchar();
    return q;
}
ui get(ui &s)
{
    return s^=s<<13,s^=s>>17,s^=s<<5,s;
}
void dfs1(int u)
{
    mxd[u]=1;
    for(auto v:g[u])
    {
        d[v]=d[u]+1,fa[v][0]=u;
        for(int i=1;i<=18;i++) fa[v][i]=fa[fa[v][i-1]][i-1];
        dfs1(v);
        mxd[u]=max(mxd[u],mxd[v]+1);
        if(mxd[v]>=mxd[son[u]]) son[u]=v;
    }
}
void dfs2(int u,int _f,int p)
{
    dfn[u]=++cnt,top[u]=_f,dn[cnt]=u,up[cnt]=p;
    if(son[u]) dfs2(son[u],_f,fa[p][0]);
    for(auto v:g[u]) if(v!=son[u]) dfs2(v,v,v);
}
int query(int u,int k)
{
    if(!k) return u;
    static int v,l;
    u=fa[u][__lg(k)],v=top[u],l=(k^(1<<__lg(k)))-(d[u]-d[v]);
    return l>=0?up[dfn[v]+l]:dn[dfn[v]-l];
}
int main()
{
    n=read(),q=read(),s=read();
    for(int i=1;i<=n;i++)
    {
        int x=read();
        if(x) g[x].push_back(i);
        else r=i;
    }
    d[r]=1,dfs1(r),dfs2(r,r,r);
    for(int i=1,now=0;i<=q;i++)
    {
        int u=(get(s)^now)%n+1,k=(get(s)^now)%d[u];
        res^=1ll*i*(now=query(u,k));
    }
    printf("%lld\n",res);
    return 0;
}

效率对比

	测试点最大用时	测试点用时总和
倍增	2.48s	6.81s
树剖	788ms	3.16s
长剖	1.07s	5.32s

倍增和长剖都需要用到 \(n\log n\) 的倍增数组，这会导致（cache miss）常数大幅增加，甚至出现了运行效率上树剖吊打长剖的情况。

更何况本题 \(q\approx 10n\) ，对于 \(n,q\) 同阶的题目（大多数都是这种），树剖足以胜任。

三、长链剖分优化\(\text{DP}\)

先拿一道例题来讲讲长链剖分的具体操作。

例2、\(\texttt{CF1009F Dominant Indices}\)

题目描述

给定一棵 \(n\) 个点的树，记 \(d(u,x)\) 为 \(u\) 子树中到 \(u\) 距离为 \(x\) 的节点数。

对 \(\forall 1\le u\le n\) ，在 \(d(u,k)\) 最大的基础上，求 \(k\) 的最小值。

数据范围

• \(1\le n\le 10^6\) 。

时间限制 \(\texttt{4.5s}\) ，空间限制 \(\texttt{500MB}\) 。

分析

\(f_{u,k}\) 表示 \(u\) 子树中，到 \(u\) 距离为 \(k\) 的节点数。转移方程为：

\[f_{u,k}=[u=0]+\sum_{v\in son(u)}f_{v,k-1}\\ \]

直接转移时间复杂度 \(\mathcal O(n^2)\) 。

注意到每个点存储的信息和链长同阶，考虑用长剖优化。

对每个点 \(u\) ，我们希望直接继承长儿子的 \(\texttt{dp}\) 数组，再暴力合并其他子节点的信息。

先考虑如何继承，对每条链动态分配内存，链上第 \(i\) 个点的头指针指向内存池中的第 \(i\) 个点。

这样 \(f_{v,k-1}\) 和 \(f_{u,k}\) 等价，相当于所有下标都会位移一位，刚好符合要求！

分配内存常见的有三种方法：

1. 用 vector 开数组，对每个链顶 resize 成当前点的链长 mxd[u] 。

   优点是非常好写，记录一下每个点的链顶和到链顶的距离即可。

   缺点是空间开销很大，本题 \(n=10^6\) 体现还不明显，如果数据范围更大很容易导致 \(\text{MLE}\) 。

2. 指针分配内存，按照长链剖分的 dfs 序确定头指针指向的位置。

   优点是空间用的很紧凑，缺点是由于用到了指针， debug 会很麻烦。

3. 记录dfn 表示偏移量，这样可以直接在一个数组里完成 \(\texttt{dp}\) ，本质和第二种方法相同。

4. 初始对根节点所在长链分配内存，在 dfs 的过程中对每个轻儿子（一定是长链链顶）分配内存。

个人感觉简单题使用第二种方法最方便，但是对于更复杂的题目第四种方法更通用。

合并时暴力枚举短链中的所有元素即可，记得实时更新答案。

由于每条链只会被合并一次，并且链长总和为 \(\mathcal O(n)\) ，因此时间复杂度 \(\mathcal O(n)\) 。

#include<bits/stdc++.h>
#define mp make_pair
using namespace std;
const int maxn=1e6+5;
int n,u,v,cnt;
int mxd[maxn],son[maxn];
int res[maxn],tmp[maxn],*f[maxn];///指针动态分配内存
vector<int> g[maxn];
void dfs1(int u,int fa)
{
    mxd[u]=1;
    for(auto v:g[u])
    {
        if(v==fa) continue;
        dfs1(v,u),mxd[u]=max(mxd[u],mxd[v]+1);
        if(mxd[v]>=mxd[son[u]]) son[u]=v;
    }
}
void dfs2(int u,int fa)
{
    f[u]=tmp+(++cnt),f[u][0]=1;
    if(son[u]) dfs2(son[u],u),res[u]=res[son[u]]+1;///数组和答案都可以直接继承
    for(auto v:g[u])
    {
        if(v==fa||v==son[u]) continue;
        dfs2(v,u);
        for(int i=1;i<=mxd[v];i++)
        {
            f[u][i]+=f[v][i-1];
            if(mp(f[u][i],-i)>=mp(f[u][res[u]],-res[u])) res[u]=i;
        }
    }
    if(f[u][res[u]]==1) res[u]=0;///前面更新答案没有考虑dis=0的贡献,这里单独补上
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d",&u,&v);
        g[u].push_back(v),g[v].push_back(u);
    }
    dfs1(1,0),dfs2(1,0);
    for(int i=1;i<=n;i++) printf("%d\n",res[i]);
    return 0;
}

---

长链剖分优化\(\text{DP}\)的操作流程已经讲完了，来说一下易错点：

• mxd 表示从 \(u\) 出发经过点数的最大值。

  对于普通的形如 \(f_{u,i}\gets f_{v,i-1}\) 的转移方程， \(u\) 的第二维下标范围为 \([0,mxd_u-1]\) 。

• 如果继承方向是反的，那么每条长链空间需要开两倍，并且链顶的头指针指向数组中部。

  按照 dfs 序分配指针的做法在这里就不适用了，我们需要在 dfs 的过程中对每条链一次性分配内存。下面是伪代码：

  void dfs2(int u,int fa)
  {
      if(son[u]) f[son[u]]=f[u]-1,dfs2(son[u],u);
      ///do something
      for(auto v:g[u])
      {
          if(v==fa||v==son[u]) continue;
          now+=mxd[v]-1,f[v]=now,now+=mxd[v];
          ///do something
      }
  }
  

  对于这种分配方式， \(u\) 的第二维下标范围仍为 \([0,mxd_u-1]\) 。

四、相关例题

例3、\(\texttt{P5904 [POI2014]HOT-Hotels 加强版}\)

题目描述

给定一棵 \(n\) 个节点的树，求无序三元组 \((i,j,k)\) 的数量，满足 \(i,j,k\) 互不相同且两两距离相等。

数据范围

• \(1\le n\le 10^5\) 。

时间限制 \(\texttt{1s}\) ，空间限制 \(\texttt{62.5MB}\) 。

分析

考虑这三个点在树上的位置关系，发现一定存在一个点 \(p\) ，满足以 \(p\) 为根时 \(i,j,k\) 两两的 \(lca\) 均为 \(p\) ，并且到 \(p\) 的距离相等。

对于原题 \(n\le 5000\) 的范围，直接枚举 \(p\) 统计答案即可。

考虑钦定以 \(1\) 号点为根，发现只有下图情况合法：

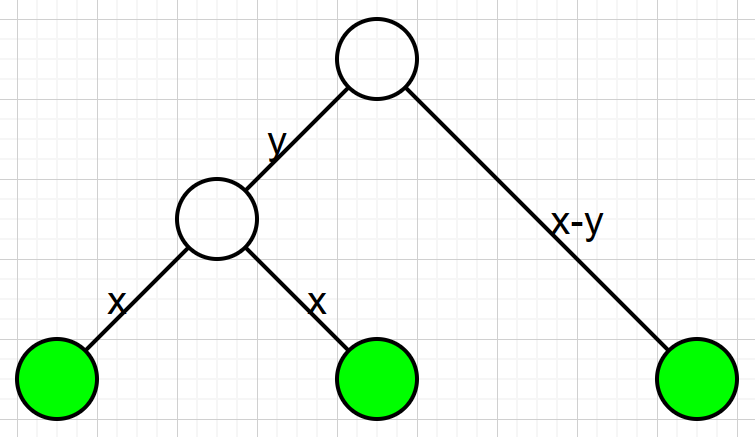
注意 \(y\) 可以等于 \(0\) ，此时要求 \(k\) 在不同于 \(i,j\) 的子树。

\(y\) 也可以等于 \(x\) ，此时 \(k\) 为 \(lca(i,j)\) 的 \(x\) 级祖先。

我们希望在最高点（ dep 最浅的点）统计答案。

令 \(f_{i,j}\) 为 \(i\) 子树中到 \(i\) 距离为 \(j\) 的点数， \(g_{i,j}\) 为 \(i\) 子树中满足 \(dep_a=dep_b\) ，上图中\(x-y=j\) 的无序点对 \((a,b)\) 个数。

转移方程如下：

\[res\gets f_{u,j-1}\cdot g_{v,j}+g_{u,j}\cdot f_{v,j-1}\\ g_{u,j}\gets f_{u,j}\cdot f_{v,j-1}+g_{v,j+1}\\ f_{u,j}\gets f_{v,j-1}\\ \]

第一行的转移是在枚举哪边出单点，哪边出二元组。

第二行的转移前者是两边分别出一个单点，后者是二元组在 \(v\) 子树内的情况。

时间复杂度 \(\mathcal O(n^2)\) ，核心代码如下：

void dfs(int u,int fa)
{
    f[u][0]=mxd[u]=1;
    for(auto v:h[u])
    {
        if(v==fa) continue;
        dfs(v,u);
        mxd[u]=max(mxd[u],mxd[v]+1);
        for(int j=1;j<=mxd[v];j++) res+=f[u][j-1]*g[v][j]+g[u][j]*f[v][j-1];
        for(int j=1;j<=mxd[v];j++) g[u][j]+=f[u][j]*f[v][j-1],g[u][j-1]+=g[v][j];
        for(int j=1;j<=mxd[v];j++) f[u][j]+=f[v][j-1];
    }
}

考虑长剖优化。

继承长儿子信息时，维护 \(f\) 是相对容易的，转移方程 \(f_{u,j}=f_{son_u,j-1}\) ，直接令 f[son[u]]=f[u]+1 即可（也就是按照 dfs 序分配空间）。

但更新 \(g\) 的方程为 \(g_{u,j-1}=g_{son_u,j}\) ，继承方向是反的，因此分配空间时 g[son[u]]=g[u]-1 ，具体可以看上面的易错点总结。

时间复杂度 \(\mathcal O(n)\) 。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+5;
int n,u,v,res;
int mxd[maxn],son[maxn];
int tmp[3*maxn],*now=tmp,*f[maxn],*g[maxn];
vector<int> h[maxn];
void dfs1(int u,int fa)
{
    mxd[u]=1;
    for(auto v:h[u])
    {
        if(v==fa) continue;
        dfs1(v,u),mxd[u]=max(mxd[u],mxd[v]+1);
        if(mxd[v]>=mxd[son[u]]) son[u]=v;
    }
}
void dfs2(int u,int fa)
{
    if(son[u]) f[son[u]]=f[u]+1,g[son[u]]=g[u]-1,dfs2(son[u],u),res+=g[u][0];
    f[u][0]=1;
    for(auto v:h[u])
    {
        if(v==fa||v==son[u]) continue;
        f[v]=now,now+=2*mxd[v]-1,g[v]=now,now+=mxd[v]+1;
        dfs2(v,u);
        for(int j=1;j<=mxd[v];j++) res+=f[u][j-1]*g[v][j]+g[u][j]*f[v][j-1];
        for(int j=1;j<=mxd[v];j++) g[u][j]+=f[u][j]*f[v][j-1],g[u][j-1]+=g[v][j];
        for(int j=1;j<=mxd[v];j++) f[u][j]+=f[v][j-1];
    }
}
signed main()
{
    scanf("%lld",&n);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%lld%lld",&u,&v);
        h[u].push_back(v),h[v].push_back(u);
    }
    dfs1(1,0);
    f[1]=now,now+=2*mxd[1]-1,g[1]=now,now+=mxd[1]+1;
    dfs2(1,0);
    printf("%lld\n",res);
    return 0;
}

例4、\(\texttt{P4292 [WC2010]重建计划}\)

双倍经验 \(\texttt{CF150E Freezing with Style}\) 的点分治做法可以看这里，现在讲一个长链剖分做法。

题目描述

给定一棵 \(n\) 个节点的树，边有边权 \(w_i\) 。

求一条边数在 \([l,r]\) 之间的路径，使得 \(w_i\) 的平均值最大。

数据范围

• \(1\le l\le r\lt n\le 10^5,1\le w_i\le 10^6\) ，保证至少存在一条合法路径。

时间限制 \(\texttt{4s}\) ，空间限制 \(\texttt{250MB}\) 。

分析

先二分答案 \(mid\) ，令 \(w_i\gets w_i-mid\) ，接下来需要判断是否存在一条长度 \(\in[l,r]\) ，权值和 \(\ge 0\) 的路径。

\(f_{u,i}\) 表示从 \(u\) 出发，走向子树内走长度为 \(i\) 的路径的最大权值。

类比重剖，按长剖的 dfs 序开一棵线段树维护答案，这样合并时枚举 \(f_{v,i}\) ，可以直接去线段树上统计答案。

注意到第二维和深度有关，用长剖优化，时间复杂度 \(\mathcal O(n\log n\log V)\) 。

转移时为避免线段树区间加的大常数，可以预处理 dis[u] 表示 \(1\to u\) 所有边的权值和，统计答案时减去相应的偏移量即可。

#include<bits/stdc++.h>
#define ls p<<1
#define rs p<<1|1
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=1e5+5;
const double eps=1e-4,inf=1e18;
int l,n,r,u,v,w,cnt;
int dfn[maxn],mxd[maxn],son[maxn],val[maxn];
double tmp[maxn],*f[maxn];
vector<pii> g[maxn];
double res,dis[maxn],mx[maxn<<2];
inline void chmax(double &x,double y)
{
    if(x<=y) x=y;
}
void modify(int p,int l,int r,int pos,double val)
{
    if(l==r) return chmax(mx[p],val);
    int mid=(l+r)/2;
    if(pos<=mid) modify(ls,l,mid,pos,val);
    else modify(rs,mid+1,r,pos,val);
    mx[p]=max(mx[ls],mx[rs]);
}
double query(int p,int l,int r,int L,int R)
{
    if(L<=l&&r<=R) return mx[p];
    if(L>r||R<l) return -inf;
    int mid=(l+r)/2;
    return max(query(ls,l,mid,L,R),query(rs,mid+1,r,L,R));
}
void dfs1(int u,int fa)
{
    mxd[u]=1;
    for(auto p:g[u])
    {
        int v=p.fi,w=p.se;
        if(v==fa) continue;
        dfs1(v,u),mxd[u]=max(mxd[u],mxd[v]+1);
        if(mxd[v]>=mxd[son[u]]) son[u]=v,val[u]=w;
    }
}
void dfs2(int u,int fa,double mid)
{
    if(!dfn[u]) dfn[u]=++cnt,f[u]=tmp+cnt;
    f[u][0]=dis[u],modify(1,1,n,dfn[u],dis[u]);
    if(son[u]) dis[son[u]]=dis[u]+val[u]-mid,dfs2(son[u],u,mid);
    for(auto p:g[u])
    {
        int v=p.fi,w=p.se;
        if(v==fa||v==son[u]) continue;
        dis[v]=dis[u]+w-mid,dfs2(v,u,mid);
        for(int i=1;i<=mxd[v];i++) chmax(res,f[v][i-1]+query(1,1,n,dfn[u]+max(l-i,0),dfn[u]+min(r-i,mxd[u]-1))-2*dis[u]);
        for(int i=1;i<=mxd[v];i++) if(f[u][i]<f[v][i-1]) f[u][i]=f[v][i-1],modify(1,1,n,dfn[u]+i,f[v][i-1]);
    }
    chmax(res,query(1,1,n,dfn[u]+l,dfn[u]+min(r,mxd[u]-1))-dis[u]);
}
bool check(double mid)
{
    for(int i=1;i<=4*n;i++) mx[i]=-inf;
    res=-inf,dfs2(1,0,mid);
    return res>=0;
}
int main()
{
    scanf("%d%d%d",&n,&l,&r);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        g[u].push_back(mp(v,w)),g[v].push_back(mp(u,w));
    }
    dfs1(1,0);
    double l=0,r=1e6;
    while(r-l>eps)
    {
        double mid=(l+r)/2;
        if(check(mid)) l=mid;
        else r=mid;
    }
    printf("%.3lf\n",l);
    return 0;
}

例5、\(\texttt{P5291 [十二省联考 2019] 希望}\)

由于题解过长，所以单开了一篇随笔，链接戳这里。

五、长链剖分优化贪心

一个经典的和长剖有关的小结论：

一棵有根树，选 \(k\) 个叶子，使得根到这些叶子的路径覆盖所有点的权值之和最大。

按照权值做长链剖分，选前 \(k\) 大的长链即可。

证明可以考虑贪心：每次选一个路径权值最大的叶子，再把整条路径权值清零，容易发现这和长剖等价。

例6、\(\texttt{BZOJ3252 攻略}\)

题目描述

给定一棵 \(n\) 个点的有根树，点有点权 \(w_i\) 。

选 \(k\) 个叶子，满足根到 \(k\) 个叶子覆盖的所有点权值之和最大。

数据范围

• \(1\le k\le n\le 2\cdot 10^5,1\le w_i\lt 2^{31}\) 。

时间限制 \(\texttt{10s}\) ，空间限制 \(\texttt{128MB}\) 。

分析

直接套用上述结论，时间复杂度 \(\mathcal O(n\log n)\) 。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+5;
int k,n,u,v,cnt,res;
int a[maxn],w[maxn];
int mxd[maxn],son[maxn];
vector<int> g[maxn];
void dfs1(int u,int fa)
{
    mxd[u]=w[u];
    for(auto v:g[u])
    {
        if(v==fa) continue;
        dfs1(v,u),mxd[u]=max(mxd[u],mxd[v]+w[u]);
        if(mxd[v]>=mxd[son[u]]) son[u]=v;
    }
}
void dfs2(int u,int fa,int top)
{
    if(u==top) a[++cnt]=mxd[u];
    if(son[u]) dfs2(son[u],u,top);
    for(auto v:g[u])
    {
        if(v==fa||v==son[u]) continue;
        dfs2(v,u,v);
    }
}
signed main()
{
    scanf("%lld%lld",&n,&k);
    for(int i=1;i<=n;i++) scanf("%lld",&w[i]);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%lld%lld",&u,&v);
        g[u].push_back(v),g[v].push_back(u);
    }
    dfs1(1,0),dfs2(1,0,1);
    sort(a+1,a+cnt+1,greater<int>());
    for(int i=1;i<=k;i++) res+=a[i];
    printf("%lld\n",res);
    return 0;
}

例7、\(\texttt{CF526G Spiders Evil Plan}\)

题目描述

给定一棵 \(n\) 个节点的树，边有边权 \(w_i\) 。

\(q\) 次询问，每次给定 \(x,y\) ，你需要选择 \(y\) 条路径，要求在包含点 \(x\) 的基础上，连通块中所有边的权值和最大。

输出最大的权值和，强制在线。

数据范围

• \(1\le n,q\le 10^5,1\le w_i\le 10^3\) 。

时间限制 \(\texttt{1s}\) ，空间限制 \(\texttt{256MB}\) 。

分析

先考虑单组询问如何处理。

以 \(x\) 为根，选择 \(2y-[deg_x=1]\) 个叶子并最大化连通块权值和，可以直接长剖解决。

注意到直径的两个端点中至少有一个一定被选，因此我们可以对两个端点分别计算答案。

假设一个端点是 \(a\) （一定是叶子），我们钦定 \(a\) 一定被覆盖，那么选 \(y\) 条路径等价于选 \(2y-1\) 个叶子，显然可以长剖预处理。

再来考虑如何限制 \(x\) 被覆盖。

如果前 \(2y-1\) 个叶子中存在 \(x\) 子树中的点，那么已经最优。

如果前 \(2y-1\) 个叶子中不存在 \(x\) 子树中的点，我们需要进行微调。

• 策略一：删除第 \(2y-1\) 条长链，加入 \(x\) 所在长链。
• 策略二：从 \(x\) 往上找到第一个在前 \(2y-1\) 条长链中的祖先，将这条长链的后半段改为 \(x\) 。

维护每个点所在长链排名 rnk ，询问时倍增向上跳即可。

时间复杂度 \(\mathcal O((n+q)\log n)\) 。

#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=1e5+5;
int n,q,w,x,y,res;
int dis[maxn];
vector<pii> g[maxn];
struct tree
{
    int cnt;
    int dis[maxn],mxd[maxn],son[maxn],fa[maxn][17];
    int s[maxn],rnk[maxn];
    pii p[maxn];
    void dfs1(int u,int f,int val)
    {
        for(auto p:g[u])
        {
            int v=p.fi,w=p.se;
            if(v==f) continue;
            fa[v][0]=u,dis[v]=dis[u]+w;
            for(int i=1;i<=16;i++) fa[v][i]=fa[fa[v][i-1]][i-1];
            dfs1(v,u,w);
            if(mxd[v]+w>=mxd[u]) son[u]=v,mxd[u]=mxd[v]+w;
        }
    }
    void dfs2(int u,int val)
    {
        if(u!=son[fa[u][0]]) p[++cnt]=mp(mxd[u]+val,u);
        for(auto p:g[u])
        {
            int v=p.fi,w=p.se;
            if(v==fa[u][0]) continue;
            dfs2(v,w);
        }
    }
    void init(int x)
    {
        dfs1(x,0,0),dfs2(x,0);
        sort(p+1,p+cnt+1,greater<pii>());
        for(int i=1;i<=cnt;i++)
        {
            s[i]=s[i-1]+p[i].fi;
            for(int j=p[i].se;j;j=son[j]) rnk[j]=i;
        }
    }
    int get(int x,int y)
    {
        for(int i=16;i>=0;i--) if(rnk[fa[x][i]]>y) x=fa[x][i];
        return fa[x][0];
    }
    int query(int x,int y)
    {
        y=min(2*y-1,cnt);
        if(rnk[x]<=y) return s[y];
        int u=get(x,y);
        return max(s[y-1]+(dis[x]-dis[get(x,y-1)])+mxd[x],s[y]-mxd[u]+(dis[x]-dis[u])+mxd[x]);
        ///如果删去第y条长链,加入x所在长链,收益get(x,y-1)->x->叶子
        ///如果将u所在长链后半段改成x,损失mxd[u],收益u->x->叶子
    }
}t1,t2;
void dfs(int u,int fa)
{
    for(auto p:g[u])
    {
        int v=p.fi,w=p.se;
        if(v==fa) continue;
        dis[v]=dis[u]+w,dfs(v,u);
    }
    if(dis[u]>dis[x]) x=u;
}
int main()
{
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d%d",&x,&y,&w);
        g[x].push_back(mp(y,w)),g[y].push_back(mp(x,w));
    }
    dis[1]=0,dfs(1,0),t1.init(x);
    dis[x]=0,dfs(x,0),t2.init(x);
    while(q--)
    {
        scanf("%d%d",&x,&y),x=(x+res-1)%n+1,y=(y+res-1)%n+1;
        printf("%d\n",res=max(t1.query(x,y),t2.query(x,y)));
    }
    return 0;
}