点分治学习笔记

一、点分治概述

参考资料：https://www.cnblogs.com/bztMinamoto/p/9489473.html。

点分治的题常见重要特征：需要处理大规模树上路径问题。

点分治的核心思想：每次选一个点，处理经过它的所有路径，然后删掉它，分成若干棵子树，继续分治。

为了保证时间复杂度，选择的这个点叫做重心。

二、树的重心

重心的定义：使得最大的一棵子树点数最小的点，称为重心。

重心的性质：

• 以重心为根，每棵子树大小均不超过总点数的一半。
• 重心到所有点的距离和最小。

注意任意一棵树至多只有两个重心，并且唯一一种有两个重心的情况如下图所示：

---

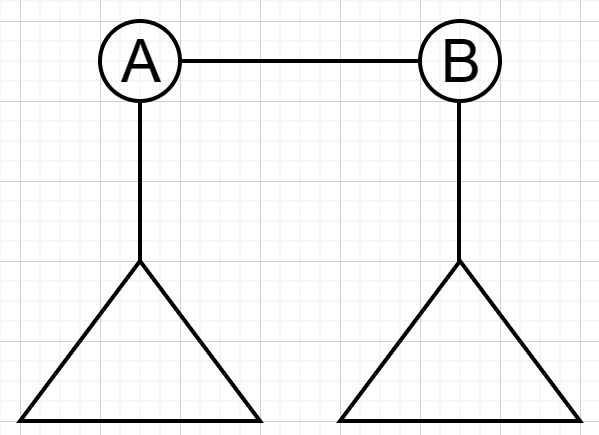
找重心只需要一个简单的树形 \(\texttt{dp}\) ：

void getroot(int u,int fa)
{
    sz[u]=1,mx[u]=0;
    for(auto v:g[u])
    {
        if(vis[v]||v==fa) continue;///常见错误 不判vis[v]
        getroot(v,u);
        sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
    }
    mx[u]=max(mx[u],all-sz[u]);///全局变量all为总点数
    if(mx[u]<mx[rt]) rt=u;
}

那分治的主函数又应该怎么写呢？先给一个伪代码：

void solve(int u)
{
    vis[u]=true;
    ///统计经过点u的所有路径信息
    for(auto v:g[u])
    {
        if(vis[v]) continue;///常见错误 不判vis[v]
        all=sz[v],getroot(v,rt=0),solve(rt);
    }
}

Warning：

• getroot 函数需要初始化 all=n,mx[0]=inf ，并且每次找重心之前需要初始化 rt=0 。

• getroot 和 solve 函数都不能访问此前已经作为重心出现（即 vis 为真）的点。

  如果只敲了一个点分治板子，统计信息啥都没干，却死循环了，不妨先检查一下有没有漏掉判断 vis 。

---

看上去感觉很对？

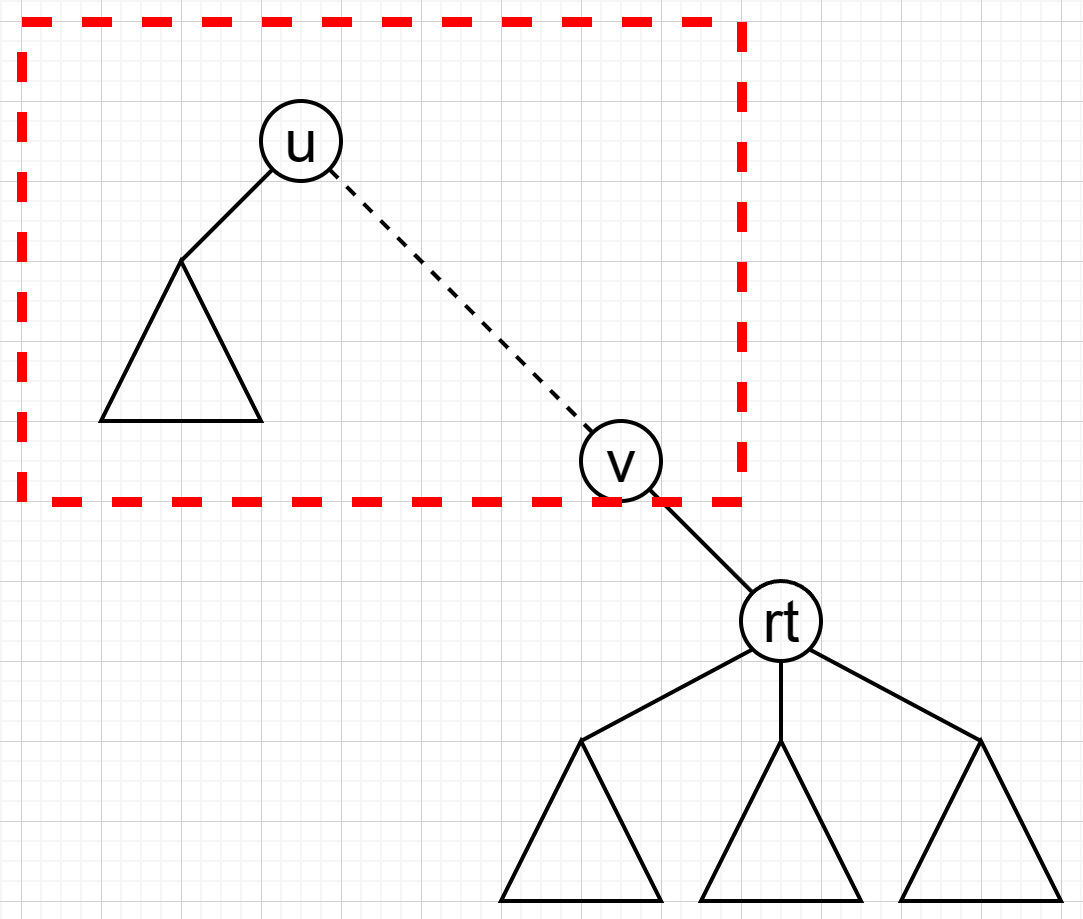
但如果出现下图这种情况，上一层以 \(u\) 为根做的树形 \(\texttt{dp}\) ，求出来重心为 \(rt\) 。那么删掉 \(rt\) 后，对于包含 \(u\) 的连通块，其真实大小为 all-sz[rt] ，但我们传入的子树大小却是 sz[v] ！

好在时间复杂度不会退化，这篇 blog 里面有详细证明。

不过递归层数不再是严格 \(\log n\) 而是 \(\mathcal O(\log n)\) ，如果数组大小和深度有关，还是需要注意一下。

---

其实正确的写法长这样：

void getroot(int u,int fa,int all)
{
    ///树形dp没啥变化
}
void solve(int u,int all)
{
    vis[u]=true;
    for(auto v:g[u])
    {
        if(vis[v]) continue;
        int nw=sz[v]<sz[u]?sz[v]:all-sz[u];
        getroot(v,rt=0,nw),solve(rt,nw);
    }
}

Warning：

• 总点数 all 需要当作参数往下传！

  否则的话，会被修改的全局变量用于 \(dfs\) ，后果你懂的。

论实用性，这种写法远没有错误的写法高；论效率，这种写法和错误写法也差不多。因此做题时几乎见不到这种写法，其实非常鸡肋。

毕竟错误的写法不仅时间复杂度没问题，而且代码实现要简洁得多，大胆用就行了！

三、点分治时间复杂度

先给结论，**点分治主体的时间复杂度为 \(\mathcal O(n\log n)\) **。（没有考虑统计信息的代价）

根据重心的性质，每分治一层，子树大小就会减半，因此**总层数为 \(\mathcal O(\log n)\) **。

由于每层每个点只会被访问一次，所以访问的总点数是 \(\mathcal O(n\log n)\) 级别。

因此，在统计信息时常常需要 \(dfs\) 整个连通块。不过千万不要惊讶，这一部分的代价仍然是 \(\mathcal O(n\log n)\) 。

预告：把 \(\sum sz=\mathcal O(n\log n)\) 理解透彻，对学习点分树有很大帮助。

温馨提示：

• 点分治主体部分常数一般很大，代码实现最好精细一点。

四、点分治相关例题

例1、\(\texttt{P3806 【模板】点分治1}\)

题目描述

给定一棵 \(n\) 个节点的树，边有边权， \(m\) 次询问树上距离为 \(k\) 的点对是否存在。

数据范围

• \(1\le n\le 10^4,1\le m\le 100,1\le k\le 10^7\) 。
• \(1\le u,v\le n,1\le w\le 10^4\) 。

时间限制 \(\texttt{200ms}\) ，空间限制 \(\texttt{500MB}\) 。

分析

所有点分治的题，分治过程都是相同的板子。所以我们只需解决如何统计信息的问题。

统计不同子树之间的贡献一般有两种方法：

• 先算任两棵子树之间的贡献，再容斥掉同一子树内部的贡献。这种方法的使用前提是统计的信息满足可减性。
• 维护已访问过的所有子树的信息（类似于前缀和），每加入一棵新的子树，先算贡献再更新前缀和数组。

记当前分治中心为 \(u\) ，我们需要统计经过 \(u\) 的所有路径中，是否存在长为 \(k\) 的路径。

注意到 dis(x,y)=dis(x,u)+dis(u,y) ，预处理 \(u\) 的每棵子树中的点到 \(u\) 的距离，用哈希表查询，然后再将这些距离加入哈希表。

注意\(m\)个询问可以一起做，但点分治只需要做一次，从而减小常数。

时间复杂度 \(\mathcal O(mn\log n)\) 。

#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=1e4+5;
int m,n,u,v,w,rt,all;
int k[maxn],mx[maxn],sz[maxn];
bool res[maxn],vis[maxn];
vector<pii> g[maxn];
vector<int> val;
unordered_set<int> h;
void getroot(int u,int fa)
{
    sz[u]=1,mx[u]=0;
    for(auto [v,w]:g[u])
    {
        if(vis[v]||v==fa) continue;
        getroot(v,u),sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
    }
    mx[u]=max(mx[u],all-sz[u]);
    if(!rt||mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa,int cur)
{
    val.push_back(cur);
    for(auto [v,w]:g[u])
    {
        if(vis[v]||v==fa) continue;
        dfs(v,u,cur+w);
    }
}
void solve(int u)
{
    vis[u]=1,h.clear(),h.insert(0);///dis(u,u)=0
    for(auto [v,w]:g[u])
    {
        if(vis[v]) continue;
        val.clear(),dfs(v,u,w);
        for(int i=1;i<=m;i++)
            for(auto j:val)
                res[i]|=h.count(k[i]-j);
        for(auto j:val) h.insert(j);
    }
    for(auto [v,w]:g[u])
    {
        if(vis[v]) continue;
        all=sz[v],getroot(v,rt=0),solve(rt);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        g[u].push_back(mp(v,w)),g[v].push_back(mp(u,w));
    }
    for(int i=1;i<=m;i++) scanf("%d",&k[i]);
    all=n,getroot(1,0),solve(rt);
    for(int i=1;i<=m;i++) printf(res[i]?"AYE\n":"NAY\n");
    return 0;
}

例2、\(\texttt{P2664 树上游戏}\)

题目描述

给定一棵 \(n\) 个节点的树，点有颜色 \(c_i\) 。

定义 \(s(i,j)\) 为树上 \(i\to j\) 的路径中不同颜色数量。

对 \(\forall 1\le i\le n\) ，求 \(sum_i=\sum_{j=1}^ns(i,j)\) 。

数据范围

• \(1\le n,c_i\le 10^5\) 。

时间限制 \(\texttt{1s}\) ，空间限制 \(\texttt{125MB}\) 。

分析

难点仍然是如何统计经过分治中心 rt 的所有路径的贡献。

本题和上一题最大的不同点，就是 \(s(i,j)\) 不再具有可加性。

对连通块中任一点 \(u\) ，如果颜色 \(c_u\) 是在 \(rt\to u\) 的路径上第一次出现，那么我们需要统计 \(c_u\) 产生的贡献；如果不是第一次出现，那我们就不管它了。

首先统计连通块对 \(sum_{rt}\) 的贡献，这个直接 dfs 一遍即可。如果 \(c_u\) 是第一次出现，其贡献为 \(sz_u\) 。

然后对于删掉 rt 后的每棵子树分别考虑。需要预处理一些东西：

• tot 表示其他子树（包含 \(rt\) ）的总点数。
• cnt[i] 表示所有从 \(rt\) 进入其他子树（包含 \(rt\to rt\) ）的路径中，包含颜色 \(i\) 的路径条数。

预处理方法为先统计连通块中整体的信息，再减去自己子树的贡献。

假设当前 dfs 到节点 \(x\) ，其他子树对 \(sum_x\) 的贡献为 \(\sum cnt_i\) 。对于 \(rt\to x\) 路径上出现的颜色 \(c\) ，还会额外贡献 \(tot-cnt_c\) 。

由于在 dfs 的过程中需要维护到根的路径上的贡献之和，所以直接把贡献当成一个参数并且在 dfs 过程中下传即可。

小细节：为保证单次时间复杂度和连通块大小同阶，我们需要统计连通块中所有出现的颜色。

时间复杂度\(\mathcal O(n\log n)\)。

本题点分治做法常数巨大，下面这份代码单个测试点跑了 \(\texttt{900ms}\) 。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+5;
int n,u,v,rt,all;
int c[maxn],mx[maxn],sz[maxn];
ll sum[maxn];
bool vis[maxn];
vector<int> g[maxn];
namespace solver
{///变量名重名太多了,单开一个结构体来统计贡献
    int rt,all,tot;///rt为分治中心,all为连通块总点数,tot为其他子树总点数
    ll tag;///tag为其他子树贡献之和,初始tag=\sum cnt_i
    int sz[maxn];///sz[i]表示子树大小
    int cnt[maxn];///cnt[i]表示从rt进入其他子树,包含颜色i的路径条数
    int exi[maxn];///dfs时标记每种颜色出现的数量
    vector<int> col;///统计连通块中出现过的颜色
    void dfs1(int u,int fa)
    {///预处理子树大小sz,总点数all,以及出现过的所有颜色col
        sz[u]=1,all++,col.push_back(c[u]);
        for(auto v:g[u]) 
        {
            if(vis[v]||v==fa) continue;
            dfs1(v,u),sz[u]+=sz[v];
        }
    }
    void dfs2(int u,int fa)
    {///预处理cnt数组,以及对sum[rt]的贡献
        if(!exi[c[u]]++) cnt[c[u]]+=sz[u],sum[rt]+=sz[u];
        for(auto v:g[u])
        {
            if(vis[v]||v==fa) continue;
            dfs2(v,u);
        }
        exi[c[u]]--;
    }
    void dfs3(int u,int fa,int op)
    {///统计信息前,容斥掉自己子树对tag和cnt的贡献;统计信息后,恢复现场
        if(!exi[c[u]]++) tag+=sz[u]*op,cnt[c[u]]+=sz[u]*op;
        for(auto v:g[u])
        {
            if(vis[v]||v==fa) continue;
            dfs3(v,u,op);
        }
        exi[c[u]]--;
    }
    void dfs4(int u,int fa,ll tag)
    {///统计连通块对子树内每个点的贡献
        if(!exi[c[u]]++) tag+=tot-cnt[c[u]];
        sum[u]+=tag;
        for(auto v:g[u])
        {
            if(vis[v]||v==fa) continue;
            dfs4(v,u,tag);
        }
        exi[c[u]]--;
    }
    void calc(int _rt)
    {
        rt=_rt,dfs1(rt,0),dfs2(rt,0);
        sort(col.begin(),col.end());
        col.erase(unique(col.begin(),col.end()),col.end());
        for(auto c:col) tag+=cnt[c];
        for(auto v:g[rt])
        {
            if(vis[v]) continue;
            tot=all-sz[v];
            cnt[c[rt]]-=sz[v],tag-=sz[v],exi[c[rt]]=1,dfs3(v,rt,-1);///准备工作
            dfs4(v,rt,tag);///统计信息
            cnt[c[rt]]+=sz[v],tag+=sz[v],dfs3(v,rt,1),exi[c[rt]]=0;///还原现场
        }
        for(auto c:col) cnt[c]=0;
        all=tag=0,col.clear();
    }
}
void getroot(int u,int fa)
{
    sz[u]=1,mx[u]=0;
    for(auto v:g[u])
    {
        if(vis[v]||v==fa) continue;
        getroot(v,u);
        sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
    }
    mx[u]=max(mx[u],all-sz[u]);
    if(mx[u]<mx[rt]) rt=u;
}
void solve(int u)
{
    vis[u]=true,solver::calc(u);
    for(auto v:g[u])
    {
        if(vis[v]) continue;
        all=sz[v],getroot(v,rt=0),solve(rt);
    }
}
int main()
{
    scanf("%d",&n),mx[0]=1e9;
    for(int i=1;i<=n;i++) scanf("%d",&c[i]);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d",&u,&v);
        g[u].push_back(v),g[v].push_back(u);
    }
    all=n,getroot(1,0),solve(rt);
    for(int i=1;i<=n;i++) printf("%lld\n",sum[i]);
    return 0;
}

例3、\(\texttt{P4075 [SDOI2016]模式字符串}\)

题目描述

\(T\) 组数据，给定一棵 \(n\) 个点的树，每个点有一个字符。

给定长为 \(m\) 的模式串 \(s\) ，求有多少个有序对 \((u,v)\) ，满足 \(u\to v\) 的所有字符拼接成的字符串是 \(s\) 重复整数次。

数据范围

• \(1\le T\le10,3\le\sum n\le 10^6,3\le\sum m\le 10^6\) 。

时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{128MB}\) 。

分析

考虑如何统计跨过分治中心 \(rt\) 的路径的贡献。

用字符串哈希判断匹配，在 \(dfs\) 的过程中维护 \(u\to rt\) 和 \(rt\to u\) 的哈希值。

维护 cnt[0/1][i] 表示已经访问过的子树中，循环匹配了 s[1~i] 和 s[i~m] 的路径条数。

注意匹配时 \(rt\) 在路径中出现了两次，因此统计答案时前后缀长度之和为 \(m+1\) 。

时间复杂度 \(\mathcal O(n\log n)\) 。

#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int maxn=1e6+5;
int m,n,u,v,rt,all,cas;
long long res;
char s[maxn],t[maxn];
int mx[maxn],sz[maxn];
ull pw[maxn],pre[maxn],suf[maxn];
bool vis[maxn];
int cnt[2][maxn];
vector<int> cur[2],vec[2],g[maxn];
void getroot(int u,int fa)
{
    sz[u]=1,mx[u]=0;
    for(auto v:g[u])
    {
        if(vis[v]||v==fa) continue;
        getroot(v,u);
        sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
    }
    mx[u]=max(mx[u],all-sz[u]);
    if(mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa,int dep,ull h0,ull h1)
{///h0表示u->rt的哈希值,h1表示rt->u的哈希值
    dep++,h0=pw[dep-1]*s[u]+h0,h1=131*h1+s[u];
    if(h0==pre[dep]) cur[0].push_back((dep-1)%m+1);
    if(h1==suf[dep]) cur[1].push_back((dep-1)%m+1);
    for(auto v:g[u])
    {
        if(vis[v]||v==fa) continue;
        dfs(v,u,dep,h0,h1);
    }
}
void calc(int rt)
{
    ///单独考虑rt->rt路径的贡献
    if(s[rt]==pre[1]) cnt[0][1]++,vec[0].push_back(1);
    if(s[rt]==suf[1]) cnt[1][1]++,vec[1].push_back(1);
    for(auto v:g[rt])
    {///每次加入一棵子树
        if(vis[v]) continue;
        cur[0].clear(),cur[1].clear();
        dfs(v,rt,1,s[rt],s[rt]);
        for(int i=0;i<=1;i++)
            for(auto l:cur[i])
                res+=cnt[i^1][m+1-l];
        for(int i=0;i<=1;i++)
            for(auto l:cur[i])
                cnt[i][l]++,vec[i].push_back(l);
    }
    for(int i=0;i<=1;i++)
    {///清空
        for(auto l:vec[i]) cnt[i][l]=0;
        vec[i].clear();
    }
}
void solve(int u)
{
    vis[u]=true,calc(u);
    for(auto v:g[u])
    {
        if(vis[v]) continue;
        all=sz[v],getroot(v,rt=0),solve(rt);
    }
}
int main()
{
    scanf("%d",&cas),mx[0]=1e9,pw[0]=1;
    for(int i=1;i<maxn;i++) pw[i]=131*pw[i-1];
    while(cas--)
    {
        scanf("%d%d%s",&n,&m,s+1),res=0;
        for(int i=1;i<=n;i++) vis[i]=false,g[i].clear();
        for(int i=1;i<=n-1;i++)
        {
            scanf("%d%d",&u,&v);
            g[u].push_back(v),g[v].push_back(u);
        }
        scanf("%s",t+1);
        for(int i=1;i<=n;i++)
        {
            int l=(i-1)%m+1;
            pre[i]=131*pre[i-1]+t[l];
            suf[i]=pw[i-1]*t[m+1-l]+suf[i-1];
        }
        all=n,getroot(1,rt=0),solve(rt);
        printf("%lld\n",res);
    }
    return 0;
}

例4、\(\texttt{P3714 [BJOI2017]树的难题}\)

题目描述

给定一棵 \(n\) 个点的树，边有颜色，总共 \(m\) 种颜色，编号 \(1\sim m\) ，第 \(i\) 种颜色权值为 \(c_i\) 。

对于一条树上路径 \(u\to v\) ，将路径上的所有边按顺序排成颜色序列，这条路径的权值为每个颜色段的颜色权值之和。

求边数在 \([l,r]\) 中的所有路径中，路径权值的最大值，保证至少有一条合法路径。

数据范围

• \(1\le n,m\le 2\cdot 10^5,0\le |c_i|\le10^4\) 。
• \(1\le l\le r\le n\) 。

时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{250MB}\) 。

分析

考虑如何统计跨过分治中心 \(rt\) 的路径的贡献。

一条 \(rt\to u\) 的链需要维护三个属性：

• len ：路径长度。
• val ：路径权值。
• col ：顶端边的颜色。

拼接两条链 \(rt\to x,rt\to y\) 的贡献可以这样算：如果 \(x\) 和 \(y\) 属于不同子树，并且 \(len_x+len_y\in[l,r]\) ，则路径权值为 \(val_x+val_y-[col_x=col_y]c_{col_x}\) 。

看上去一脸不可做的样子。

\(\texttt{Key observation}\) ：如果 \(x\) 和 \(y\) 的 \(col\) 不同，则路径权值为val[x]+val[y]，并且 \(x\) 和 \(y\) 互相独立！

同时还有一个性质：如果x和y的颜色不同，那么一定属于不同子树。

每次加入一种颜色的所有链，同时询问长度在[l-len[x],r-len[x]]之间的所有已经访问过的链的权值最大值，线段树维护即可统计异色链的贡献。

同色链做法和上面几乎相同，每次加入一棵子树，即可保证 \(x\) 和 \(y\) 属于不同子树。

点分治的题目每次 calc 完毕都是要清空的，但清空是个技术活。

方法一：用 queue/stack/vector 记录插入线段树的信息，最后一个个modify回来。

方法二：用 queue/stack/vector 记录访问到的节点，最后一起清空。

方法三：线段树多打一个覆盖 cov 标记或时间戳 tim 标记。

一般来说，方法一和方法二是通用的，如果维护的信息可逆（比如区间加）则更推荐用方法一。而方法三最为简洁，只需在递归访问到某节点时执行 if(f[p].tim!=tim) clean(p); 即可。

下面代码中用的是方法二。

时间复杂度 \(\mathcal O(n\log^2n)\) 。

#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,ll>
using namespace std;
const int maxn=2e5+5,maxm=4e5+5;
const ll inf=1e18;
int l,r,m,n,u,v,w,rt,all,tot=1;
ll res=-inf;
int head[maxn],to[maxm],nxt[maxm],val[maxm];
int mx[maxn],sz[maxn];
bool vis[maxn];
int c[maxn];
vector<int> col,vec[maxn];///col存储出现的颜色,vec[i]存储颜色为i的所有子树
vector<pii> h[maxn];///h[x]以pair<len,val>的形式存储x子树中所有链
void chmax(ll &x,ll y)
{
    if(x<=y) x=y;
}
struct sgmt
{
    #define ls p<<1
    #define rs p<<1|1
    int top,st[20*maxn];
    struct node
    {
        int l,r;
        ll mx;
    }f[4*maxn];
    void pushup(int p)
    {
        f[p].mx=max(f[ls].mx,f[rs].mx);
    }
    void build(int p,int l,int r)
    {
        f[p].l=l,f[p].r=r;
        if(l==r) return f[p].mx=-inf,void();
        int mid=(l+r)/2;
        build(ls,l,mid);
        build(rs,mid+1,r);
        pushup(p);
    }
    void modify(int p,int pos,ll val)
    {
        st[++top]=p;
        if(f[p].l==f[p].r) return chmax(f[p].mx,val);
        int mid=(f[p].l+f[p].r)/2;
        if(pos<=mid) modify(ls,pos,val);
        else modify(rs,pos,val);
        pushup(p);
    }
    ll query(int p,int l,int r)
    {
        if(l<=f[p].l&&f[p].r<=r) return f[p].mx;
        if(l>f[p].r||r<f[p].l) return -inf;
        return max(query(ls,l,r),query(rs,l,r));
    }
    void clean()
    {
        while(top) f[st[top--]].mx=-inf;
    }
}t1,t2;
void addedge(int u,int v,int w)
{
    nxt[++tot]=head[u],to[tot]=v,val[tot]=w,head[u]=tot;
}
void getroot(int u,int fa)
{
    sz[u]=1,mx[u]=0;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(vis[v]||v==fa) continue;
        getroot(v,u);
        sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
    }
    mx[u]=max(mx[u],all-sz[u]);
    if(mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa,int len,ll val,int col,int x)
{
    h[x].push_back(mp(len,val));
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i],w=::val[i];
        if(vis[v]||v==fa) continue;
        dfs(v,u,len+1,val+(w!=col)*c[w],w,x);
    }
}
void calc(int rt)
{
    for(int i=head[rt];i;i=nxt[i])
    {
        int v=to[i],w=val[i];
        if(vis[v]) continue;
        col.push_back(w),vec[w].push_back(v);
        dfs(v,rt,1,c[w],w,v);
    }
    sort(col.begin(),col.end());
    col.erase(unique(col.begin(),col.end()),col.end());
    t1.modify(1,0,0);///别忘了根节点的贡献
    for(auto u:col)
    {
        for(auto x:vec[u])
        {
            for(auto p:h[x])
            {
                chmax(res,p.se+t1.query(1,l-p.fi,r-p.fi));
                chmax(res,p.se+t2.query(1,l-p.fi,r-p.fi)-c[u]);
            }
            for(auto p:h[x]) t2.modify(1,p.fi,p.se);
        }
        t2.clean();
        for(auto x:vec[u])
            for(auto p:h[x])
                t1.modify(1,p.fi,p.se);
    }
    for(auto u:col)
    {
        for(auto x:vec[u]) h[x].clear();
        vec[u].clear();
    }
    col.clear(),t1.clean();
}
void solve(int u)
{
    vis[u]=true,calc(u);
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(vis[v]) continue;
        all=sz[v],getroot(v,rt=0),solve(rt);
    }
}
int main()
{
    scanf("%d%d%d%d",&n,&m,&l,&r),mx[0]=1e9;
    for(int i=1;i<=m;i++) scanf("%d",&c[i]);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        addedge(u,v,w),addedge(v,u,w);
    }
    t1.build(1,0,n-1),t2.build(1,0,n-1);
    all=n,getroot(1,0),solve(rt);
    printf("%lld\n",res);
    return 0;
}

例5、\(\texttt{CF150E Freezing with Style}\)

题目描述

给定一棵 \(n\) 个点的树，边有边权 \(w_i\) 。

求一条边数在 \([l,r]\) 中的路径，使得路径上边权中位数最大，并输出路径的两个端点。

注：若边权从大到小排序为 \(b_1,\cdots,b_x\) ，本题中位数定义为 \(b_{\lfloor\frac{x+1}2\rfloor}\) 。

数据范围

• \(1\le n\le 10^5,0\le w_i\le 10^9\) 。
• \(1\le l\le r\le n\) ，保证至少有一条合法路径。

分析

本题涉及到了一个新的套路：单调队列按秩合并。

其实这个套路和点分治关系不大，但是点分治和单调队列的搭配比较常见所以放在这里讲了。

上一题可以用这个套路做到 \(\mathcal O(n\log n)\) 的时间复杂度，但是线段树做法好想好写就没讲。

中位数常见转化：先二分答案，给 \(\lt mid\) 的边赋权值 \(-1\) ，给 \(\ge mid\) 的边赋权值 \(1\) 。

于是我们只需判断是否存在一条边数 \(\in[l,r]\) 的路径，权值和非负。

考虑点分治，每次统计跨过分治中心 \(rt\) 的路径。

显然每条到 \(rt\) 的路径可以用长度 len 和权值 val 两个属性表示。

如果按照上一题的套路，二分答案 & 点分治 & 线段树总共 \(3\) 只 \(\log\) ，过不去。

对于 len 相同的路径，显然只需要保留 val 最大的一条。并且 len 的上界（记为 mxd ）实际上就是从 \(rt\) 往子树中走的最大深度。

用一个长为 mxd 的数组存储访问过的子树的信息，注意到在 len 减小的过程中， \([l-len,r-len]\) 是一个滑动窗口，并且我们的目标是求每个窗口中的最大值。

因此，用单调队列代替线段树，就可以去掉一只 \(\log\) 。

但是别忘了单调队列初始化的复杂度！

每次我们需要把 len 在 \([l,r]\) 中的所有元素塞入单调队列，如果先碰到一个 mxd 非常大的子树，后面跟着一堆 mxd 比较小的节点显然是不划算的。

因此我们需要把所有子树按 mxd 升序排序后依次加入，初始化时间复杂度为 \(\mathcal O(\sum mxd)=\mathcal O(\sum sz)=\mathcal O(n\log n)\) 。

于是单次点分治的时间复杂度为 \(\mathcal O(n\log n)\) ，套上最外层二分以后时间复杂度为 \(\mathcal O(n\log^2n)\) 。

为了减小点分治的巨大常数带来的影响，我们只在预处理时执行一次点分治，存储每个连通块的重心并按 mxd 排序，二分过程中不再执行点分治的主体过程。

#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=1e5+5,maxm=2e5+5,inf=1e9+5;
int l,r,n,u,v,w,x,rt,all,flg,lim,tot=1;
pii res;
int head[maxn],to[maxm],val[maxm],nxt[maxm];
int mx[maxn],sz[maxn];
bool vis[maxn];
int q[maxn];
pii f[maxn],now[maxn];
vector<int> g[maxn];
vector<pair<int,pii>> s[maxn];
void addedge(int u,int v,int w)
{
    nxt[++tot]=head[u],to[tot]=v,val[tot]=w,head[u]=tot;
}
void getroot(int u,int fa)
{
    sz[u]=1,mx[u]=0;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(vis[v]||v==fa) continue;
        getroot(v,u);
        sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
    }
    mx[u]=max(mx[u],all-sz[u]);
    if(mx[u]<mx[rt]) rt=u;
}
void dfs1(int u,int fa,int dis,int &mxd)
{
    mxd=max(mxd,dis);
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(vis[v]||v==fa) continue;
        dfs1(v,u,dis+1,mxd);
    }
}
void prework(int u)
{
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i],w=val[i],mxd=0;
        if(vis[v]) continue;
        dfs1(v,u,1,mxd);
        s[u].push_back(mp(mxd,mp(v,w)));
    }
    sort(s[u].begin(),s[u].end());
}
void solve(int u)
{
    vis[u]=true,prework(u);
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(vis[v]) continue;
        all=sz[v],getroot(v,rt=0),g[u].push_back(rt),solve(rt);
    }
}
void chmax(pii &a,pii b)
{
    if(a<b) a=b;
}
void dfs3(int u,int fa,int dis,int val)
{
    chmax(now[dis],mp(val,u));
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i],w=::val[i];
        if(vis[v]||v==fa) continue;
        dfs3(v,u,dis+1,val+(w>=lim?1:-1));
    }
}
void calc(int u)
{
    int cur=0;
    f[0]=mp(0,u);
    for(auto p:s[u])
    {
        int v=p.se.fi,w=p.se.se,mxd=p.fi;
        for(int i=0;i<=mxd;i++) now[i]=mp(-inf,0);
        dfs3(v,u,1,w>=lim?1:-1);
        int h=1,t=0;
        for(int i=max(l-mxd,0);i<=min(r-mxd,cur);i++)
        {
            while(h<=t&&f[q[t]]<=f[i]) t--;
            q[++t]=i;
        }
        for(int i=mxd,j=r-i;i>=0;i--,j++)
        {
            while(h<=t&&q[h]<l-i) h++;
            if(j>=0&&j<=cur)
            {
                while(h<=t&&f[q[t]]<=f[j]) t--;
                q[++t]=j;
            }
            if(h<=t&&f[q[h]].fi+now[i].fi>=0)
            {
                flg=1,res=mp(f[q[h]].se,now[i].se);
                return ;
            }
        }
        for(int i=cur+1;i<=mxd;i++) f[i]=mp(-inf,0);
        cur=mxd;
        for(int i=0;i<=cur;i++) chmax(f[i],now[i]);
    }
}
void dfs2(int u)
{
    if(flg) return ;
    vis[u]=true,calc(u);
    for(auto v:g[u]) dfs2(v);
}
bool check(int mid)
{
    flg=0,lim=mid;
    for(int i=1;i<=n;i++) vis[i]=false;
    dfs2(x);
    return flg;
}
int main()
{
    scanf("%d%d%d",&n,&l,&r),mx[0]=inf;
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        addedge(u,v,w),addedge(v,u,w);
    }
    all=n,getroot(1,0),solve(x=rt);
    int L=-1,R=inf;
    while(R-L>1)
    {
        int mid=(L+R)/2;
        if(check(mid)) L=mid;
        else R=mid;
    }
    printf("%d %d\n",res.fi,res.se);
    return 0;
}

例6、\(\texttt{P4886 快递员}\)

题目描述

给定一棵 \(n\) 个点的树，边有边权 \(w_i\) 。

对固定的点 \(c\) ，定义点对 \((u,v)\) 的花费为 \(dis_{u,c}+dis_{c,v}\) 。

给定 \(m\) 个点对 \((u_i,v_i)\) ，求如何选取 \(c\) ，使得所有点对花费最大值最小。

数据范围

• \(1\le n,m\le 10^5\) 。

时间限制 \(\texttt{1s}\) ，空间限制 \(\texttt{128MB}\) 。

分析

本题涉及到了点分治的一类常见套路：点分治重心移动。

写完本题还可以去看看CF566C、P3345。

先来思考一个问题：如果把 \(c\) 换成某个邻点 \(c'\) ，答案会如何变化？

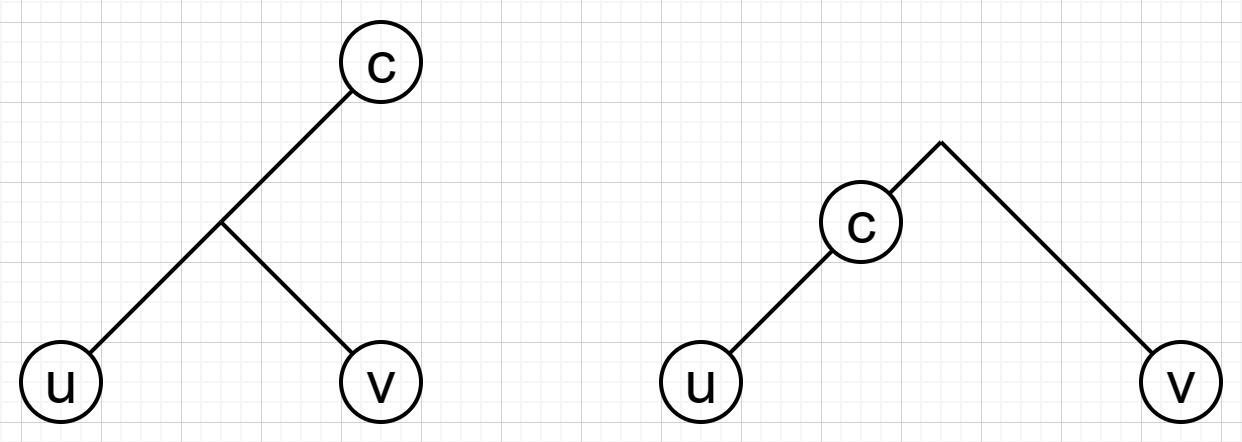
假设花费最大的一个点对为 \((u_i,v_i)\) ，分如下两种情况讨论。

• 对于左图的情况， \(u,v\) 在 \(c\) 的同一棵子树内，把 \(c\) 换成在 \(u,v\) 子树方向上的邻点可能最优。

  注意是可能最优，因为移动可能导致花费最大的点对发生变化。

• 对于右图的情况， \(u,v\) 在 \(c\) 的不同子树中，此时答案无法继续减小，输出这一对 \((u,v)\) 的花费即可。

  更准确的说法是，如果 \(c\) 在 \(u\to v\) 的路径上（包含 \(u,v\) ），那么答案无法继续减小。

如果花费最大的\((u_i,v_i)\)不只一对，和上面的分析类似，如果存在两个点对在 \(c\) 的不同子树中，那么答案也无法继续减小。

逐步尝试移动 \(c\) ，把访问过的所有点的答案取 \(\min\) ，就是最终答案。

伪代码如下：

void solve(int u)
{
    vis[u]=true;
    ///dfs求最大的点对花费,并对res取min
    ///如果答案无法继续减小,直接return
    ///否则求出往哪棵子树v递归可能使答案变优,注意这样的v只有一个
    if(vis[v]) return ;///不能走回头路
    solve(v);
}
///最后输出res即可

这个做法的时间复杂度仍为 \(\mathcal O(nm)\) 。

其中 \(n\) 表示移动次数，当树退化为链时，移动次数可以卡满 \(\mathcal O(n)\) 。

我们花费了 \(\mathcal O(m)\) 的代价，却只让 \(c\) 移动了一步，是不是有点浪费？

而减少移动次数的方法，就是点分治。

每次不再只移动一步，而是移到所在连通块的重心。这样每次候选点集的大小就会减半，只需要 \(\log n\) 次移动就一定可以找到最优的\(c\)。

点分治重心移动的伪代码如下：

void solve(int u)
{
    if(vis[u]) return ;
    vis[u]=true;
    ///dfs求最大的点对花费,并对res取min
    ///如果答案无法继续减小,直接return
    ///否则求出往哪棵子树递归最优,记为v
    if(vis[v]) return ;///不能走回头路
    ///否则继续递归v所在连通块的重心
}

时间复杂度 \(\mathcal O((n+m)\log n)\) 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5,maxm=2e5+5,inf=1e9;
int m,n,u,v,w,rt,all,res=inf,tot=1;
int x[maxn],y[maxn];
int head[maxn],to[maxm],val[maxm],nxt[maxm];
int mx[maxn],sz[maxn];
bool vis[maxn];
int d[maxn],bel[maxn];
void addedge(int u,int v,int w)
{
    nxt[++tot]=head[u],to[tot]=v,val[tot]=w,head[u]=tot;
}
void getroot(int u,int fa)
{
    sz[u]=1,mx[u]=0;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(vis[v]||v==fa) continue;
        getroot(v,u);
        sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
    }
    mx[u]=max(mx[u],all-sz[u]);
    if(mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa,int dis,int x)
{
    d[u]=dis,bel[u]=x;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i],w=val[i];
        if(v==fa) continue;
        dfs(v,u,dis+w,x);
    }
}
void solve(int u)
{
    vis[u]=true,d[u]=bel[u]=0;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i],w=val[i];
        dfs(v,u,w,v);
    }
    int mx=0;
    vector<int> vec;
    for(int i=1;i<=m;i++)
    {
        int cur=d[x[i]]+d[y[i]];
        if(cur>mx) mx=cur,vec.clear(),vec.push_back(i);
        else if(cur==mx) vec.push_back(i);
    }
    res=min(res,mx);
    int v=0;
    for(auto p:vec)
    {
        if(x[p]==u||y[p]==u||bel[x[p]]!=bel[y[p]]) return ;
        if(v&&bel[x[p]]!=v) return ;
        v=bel[x[p]];
    }
    if(vis[v]) return ;
    all=sz[v],getroot(v,rt=0),solve(rt);
}
int main()
{
    scanf("%d%d",&n,&m),mx[0]=inf;
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        addedge(u,v,w),addedge(v,u,w);
    }
    for(int i=1;i<=m;i++) scanf("%d%d",&x[i],&y[i]);
    all=n,getroot(1,0),solve(rt);
    printf("%d\n",res);
    return 0;
}