数据结构（4） 线段树

线段树真的是一个非常好用的算法。

线段树基础

以下描述均以线段树维护区间和为例。

基本结构

先看图（图源自链接）

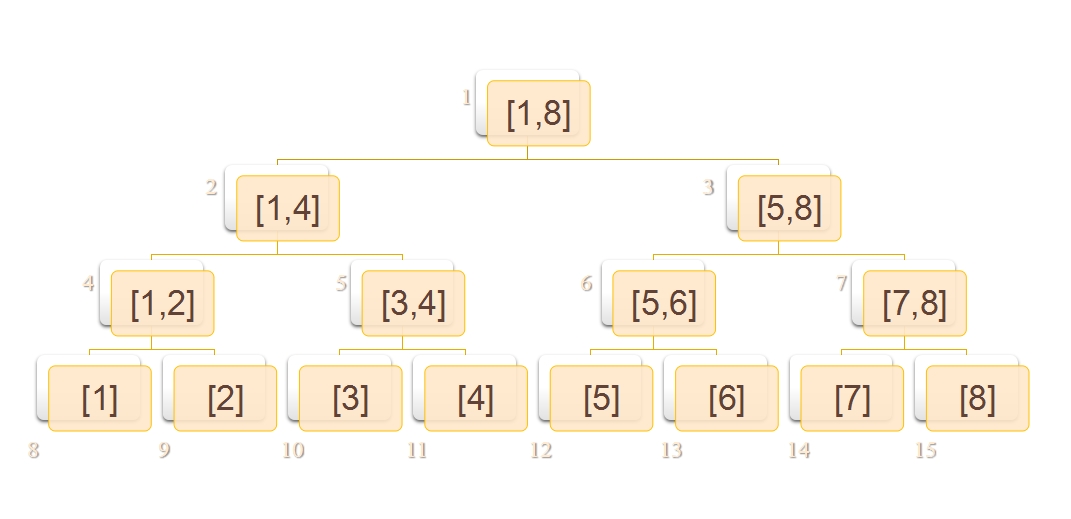
线段树就是这样一种结构，树上的每个节点都代表了原数组中的连续一段，每个节点维护了这一段的一些数据。

线段树将每个长度不为 \(1\) 的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。

最基本的线段树包含以下几个概念：

1. 线段树每个节点表示一个区间
2. 线段树的唯一根节点表示整个区间统计范围，如 \([1,N]\)。
3. 线段树的每个叶节点表示一个长度为 \(1\) 的元区间，如 \([x,x]\)。
4. 线段树上的每个节点 \([l,r]\)，它的左子节点是 \([l,mid]\)，右子节点是 \([mid+1,r]\)，其中 \(mid=(l+r)/2\)。

建树

不断从中点分割成两段，直到该节点为叶子节点时，进行赋值并将两段合并为父节点。

void build(ll l,ll r,ll o){
	sc[o]=r-l+1;
	if(l==r){
		t[o]=a[l];
		return;
	}
	else {
		ll mid=(l+r)>>1;
		build(l,mid,o<<1);
		build(mid+1,r,o<<1|1);
		push_up(o);
	}
}

区间修改

我们引入一个数组，也是线段树的核心：懒标记。

懒标记，简单来说，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。每次执行修改时，我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。

在修改时，如果该节点维护的区间，完全属于修改区间，我们就可以直接修改这个节点，并给这个节点打上懒标记，在需要他的子节点的数据时把懒标记下放。

void change(ll l,ll r,ll L,ll R,ll k,ll o){
	if(l>=L && r<=R)atg(o,k);
	else {
		push_down(o);
		int mid=(l+r)>>1;
		if(L<=mid)change(l,mid,L,R,k,o<<1);
		if(mid<R)change(mid+1,r,L,R,k,o<<1|1);
		push_up(o);
	}
}

区间查询

不断二分序列合并两者信息即可。

记得随时下放懒标记。

ll ask(ll l,ll r,ll L,ll R,ll o){
	if(l>=L && r<=R)return t[o];
	else{
		push_down(o);
		ll mid=(l+r)>>1;
		ll res=0;
		if(L<=mid)res+=ask(l,mid,L,R,o<<1);
		if(mid<R)res+=ask(mid+1,r,L,R,o<<1|1);
		return res;
	}
}

tip

我们为了方便代码的编写，我们会将一些在线段树模板中使用频率高的语句封装起来：

void atg(ll o,ll k){
	t[o]+=sc[o]*k;
	tg[o]+=k;
}
void push_up(ll o){
	t[o]=t[o<<1]+t[o<<1|1];
}
void push_down(ll o){
	if(tg[o]){
		atg(o<<1,tg[o]);
		atg(o<<1|1,tg[o]);
		tg[o]=0;
	}
}

其中，\(atg()\) 是单点修改，\(push\_up\) 是修改子节点后把新信息合并到父节点，\(push\_down\) 是将懒标记下放的操作。

还有一个 zkw 线段树，常数更小，但本质复杂度没变。

由于线段树的树形结构，所以在关于线段树的数组是需要开四倍空间的。

Code.

#include<bits/stdc++.h>
#define endl "\n"
#define pb push_back
#define mkp make_pair

using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value 
const int inf=2147483647;
const int mod=1e9+7;
const int N=1e5+5;
ll t[N*4],tg[N*4],a[N],sc[N*4];


//function 
void atg(ll o,ll k){
	t[o]+=sc[o]*k;
	tg[o]+=k;
}
void push_up(ll o){
	t[o]=t[o<<1]+t[o<<1|1];
}
void push_down(ll o){
	if(tg[o]){
		atg(o<<1,tg[o]);
		atg(o<<1|1,tg[o]);
		tg[o]=0;
	}
}
void build(ll l,ll r,ll o){
	sc[o]=r-l+1;
	if(l==r){
		t[o]=a[l];
		return;
	}
	else {
		ll mid=(l+r)>>1;
		build(l,mid,o<<1);
		build(mid+1,r,o<<1|1);
		push_up(o);
	}
}
void change(ll l,ll r,ll L,ll R,ll k,ll o){
	if(l>=L && r<=R)atg(o,k);
	else {
		push_down(o);
		int mid=(l+r)>>1;
		if(L<=mid)change(l,mid,L,R,k,o<<1);
		if(mid<R)change(mid+1,r,L,R,k,o<<1|1);
		push_up(o);
	}
}
ll ask(ll l,ll r,ll L,ll R,ll o){
	if(l>=L && r<=R)return t[o];
	else{
		push_down(o);
		ll mid=(l+r)>>1;
		ll res=0;
		if(L<=mid)res+=ask(l,mid,L,R,o<<1);
		if(mid<R)res+=ask(mid+1,r,L,R,o<<1|1);
		return res;
	}
}


 
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0); 
	
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	
	ll n,q;
	cin>>n>>q;
	for(int i=1;i<=n;i++)cin>>a[i];
	
	build(1,n,1);
	
	while(q--){
		int opt;
		cin>>opt;
		if(opt==1){
			ll x,y,k;
			cin>>x>>y>>k;
			change(1,n,x,y,k,1);
		}
		else {
			ll x,y;
			cin>>x>>y;
			cout<<ask(1,n,x,y,1)<<endl;
		}
	}
	
	
	
	return 0;
}

动态开点线段树

注意到我们在使用线段树时，有很多时候我们并不需要那么多点，我们可以在一个点真正被需要到的时候再建立它。实际实现我们只需要对每个点新建一个数组标记他的左右子节点即可。

支持区间修改区间查询 ，但是实际开点我脑测了一下好像优化的不多。

动态开点线段树有着一些优点，比如说当你让某个节点继承另一个节点的左儿子或者右儿子的时候，你可以不用新建一棵线段树，而是直接将该节点的左右儿子赋成那个节点的左右儿子就行了。

动态开点线段树的主要应用是一些可持久化数据结构和一些不可离散化的东西。