最优前缀码
1.问题
给定字符集C={x1,x2,...xn}和每个字符的频率f(xi),求关于C的最优前缀码
2.解析
构造最优前缀码的贪心算法就是哈夫曼编码。
下面给出证明哈夫曼编码是求解最优前缀码的其中一种解法。
引理1:给定字符集C={x1,x2,..xn}以及每个字符的频率f(xi),以此来构造哈夫曼树,假设xi和xj是出现频率最小的两个节点。
则这两个节点是兄弟节点,同时,这两个节点在二叉树中的深度不小于其他任意一个叶子节点的深度。
证明:如果xi和xj不是深度最深的节点,则假设存在一点xk的深度大于xi和xj,根据哈夫曼树的构造规则,
xk的出现频率是小于xi和xj与所给的条件相冲突。同时因为xi和xj是最小的两个节点,那么除去xi之后就会选择xj那么他们必是兄弟节点。
定理1:哈夫曼编码是最优的
下面用数学归纳法证明。
1.当所给的点数为两个的时候,即n=2时,由于树只有两种可能,两种树 在哈夫曼树下的最小权重外部路径是一样的。
2.假设n-1个叶子节点的哈夫曼树是成立的。
推导:设f(x1)<f(x2)<...<f(xn),灵v是x1和x2的父亲节点,由引理1知,不存在叶子节点深度大于x1和x2的深度。
若存在,我们可以将他们与w1和w2进行交换,得到更小的WPL,按例如以下方式得到到二叉树T:以结点V'替换结点V, 当中V'的权重是x1+x2,则T'是对应于{w1+w2,w3,...,wn}的一棵哈夫曼树。依据归纳如果。T具有最小权重外部路径,T是最优的(EPW最小)。在T'的结点V'上加入叶结点x1, x2。可得T。则T是具有最小权重外部路径的哈夫曼树。
可得定理一是正确的。
下面来看哈夫曼构造哈夫曼树的过程。
实例{2,3,4,4,5,7,8}

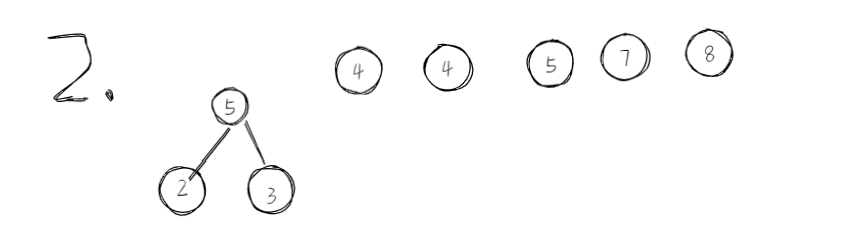
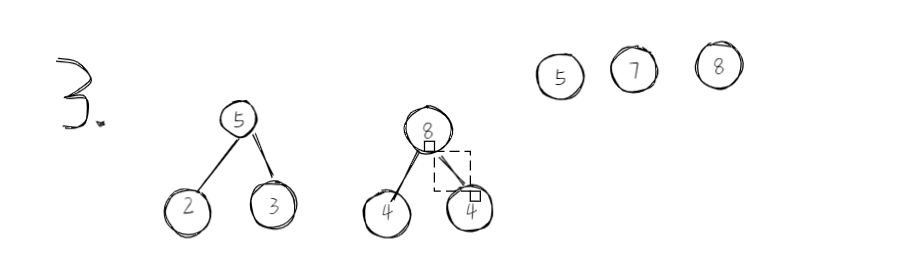
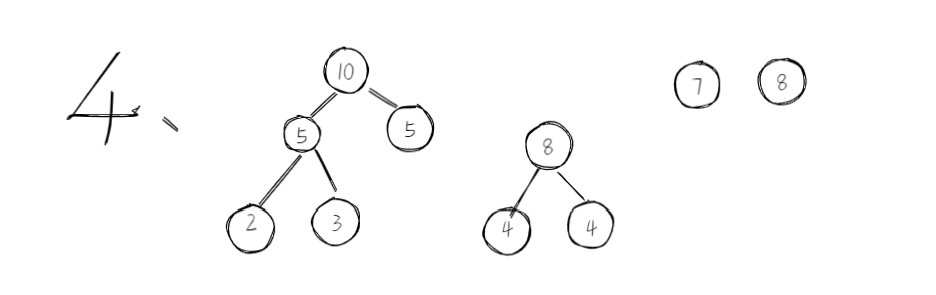
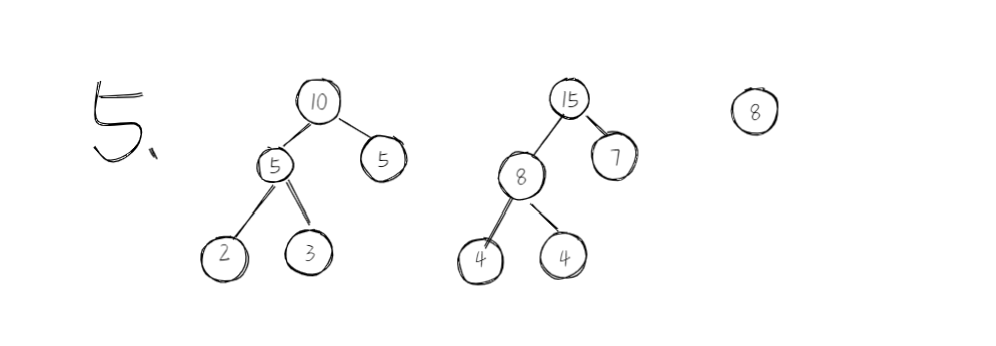
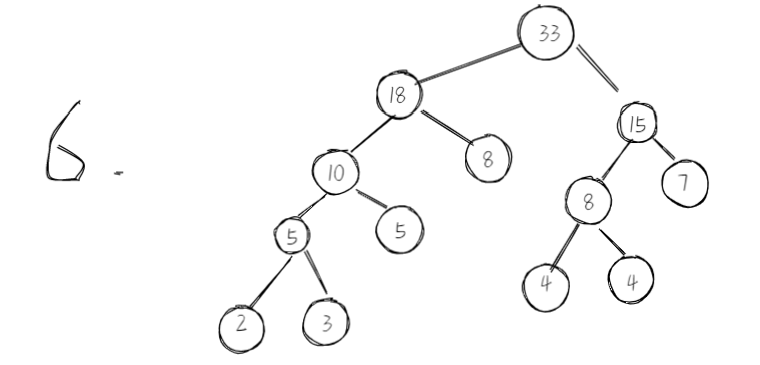
3.设计
4.分析
O(nlogn)频率排序;for 循环 O(n),插入操作 O(logn),算法时间复杂 度是 O(nlogn)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号