Deep Learning with Gaussian Differential Privacy
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!
Bu, Z., Dong, J., Long, Q., & Weijie, S. (2020). Deep Learning with Gaussian Differential Privacy. Harvard Data Science Review. https://doi.org/10.1162/99608f92.cfc5dd25

摘要
深度学习模型通常在包含敏感信息(如个人的购物交易、个人联系人和医疗记录)的数据集上进行训练。因此,越来越重要的工作已经寻求训练神经网络,受到隐私约束,这些约束由不同的隐私或其基于分歧的松弛来指定(fiff)。然而,这些隐私定义(Privacy Defi)在处理某些重要的基元(合成和子采样)方面存在弱点,从而给出了松散或复杂的训练神经网络的隐私分析。在这篇文章中,我们考虑最近提出的隐私定义,称为f-dififf隐私[18],用于训练神经网络的Re-fiNed隐私分析。利用f-ff差分隐私性在处理合成和次采样方面的吸引力,本文推导出随机梯度下降和ADAM在训练深度神经网络时所用的隐私性保证的解析表达式,而不需要像[3]那样开发复杂的技术。我们的结果表明,f-Diffential隐私框架允许新的隐私分析,它改进了先前的分析[3],这反过来又建议调整神经网络的某些参数,以便在不违反隐私预算的情况下获得更好的预测精度。这些理论上的改进被我们在一系列任务中的实验所证实,这些任务在图像分类fi定位、文本分类定位和推荐系统中都得到了验证。TensorFlow Privacy库中公开提供了计算这些实验的隐私成本的Python代码。
引言
在机器学习的许多应用中,数据集包含有关个人的敏感信息,如位置、个人联系人、媒体消费和医疗记录。利用机器学习算法的输出,对手可能能够识别数据集中的一些个人,从而呈现严重的隐私问题。这一现实引发了开发保护隐私的数据分析方法的广泛而紧迫的呼吁。因此,在许多fi领域-统计学、密码学、机器学习和法律-的学术文献中已经进行了大量的调查,以保护数据分析中的隐私。沿着这条路线,研究和研究人员一再提出,有必要对隐私进行严格而全面的定义(defffinition)。在其他方面,研究人员质疑是否使用隐私defi定义给出了可解释的隐私保证,如果是这样的话,该隐私defi定义是否允许可选的defi定义中的私有模型的高精确度。
具体地说,匿名化作为一种句法上的和特别的隐私概念已经被证明通常不能保证隐私。例如,匿名化的NetfiIX挑战数据集中的恐同个体的identifl阳离子[45],以及当时的马萨诸塞州州长的健康记录在公开的匿名医疗数据集中的identifi阳离子[56]。
在此背景下,(ε,δ)-Dierential Privacy(DP)作为一种数学上严格的隐私定义应运而生[23]。今天,这个definition已经发展成为私有数据分析的fiRM基础,其应用程序由谷歌[26]、苹果[5]、微软[16]和美国人口普查局[4]部署。尽管(ε,δ)-DP在学术文献和行业中都很受欢迎,但它的通用性不足以处理组合,这可能是统计隐私中最基本的原语。例如,深度神经网络的训练过程实际上是由许多被称为随机梯度下降的原始构件组成的(ff)。然而,在(ε,δ)-DP意义上适度的隐私预算下,如何保持深度学习的高预测精度并不清楚。这需要对(ε,δ)-DP框架中的组成进行严格的隐私分析。事实上,对深度学习中隐私成本的分析直到最近才开始使用一种名为时刻会计的复杂技术[3]。
理想情况下,我们希望有一个隐私定义(finition),允许以原则性的方式重新对各种算法进行隐私分析,而不需要求助于复杂的技术。进行RefiNed隐私分析不仅可以增强模型的可信性,而且可以通过牺牲ff隐私来换取效用来提高预测精度。一个可能的候选者是fdifferential Privacy,这是董、罗斯和苏最近提出的(ε,δ)-DP的一种放宽[18]。这种新的隐私定义忠实地保留了对差异隐私的假设检验解释,并且可以无损地推理与差异隐私相关的常见基元,包括合成、通过次采样的隐私放大以及组隐私。(fi)该定义忠实地保留了对差异隐私的假设检验解释,并且可以无损地推理与差异隐私相关的常见基元,包括合成、通过次采样的隐私放大和组隐私。此外,fdp还包括一个规范的单参数家族,称为高斯微分隐私(Gdp)。值得注意的是,gdp是焦点隐私定义(finition),因为中心极限定理表明,私有算法组合的隐私保证近似等于区分两个移位的正态分布。
1个
值得注意的是,训练深度学习模型一直是测试隐私检测的重要基准,因为其隐私分析的严密性关键取决于是否能紧密地说明合成和次抽样(Definition)。
封闭形式的隐私界限。在f-dp框架中,训练神经网络所造成的总体隐私损失允许服从闭合形式的表达式。相反,通过矩会计进行的隐私分析必须通过数值计算来完成[3],这种早期方法的隐含性质可能会阻碍我们理解调整参数aff是如何影响隐私界限的。这将在3.1节中讨论。
更强有力的隐私保障。f-dp方法比以前的方法[3]提供了更强的隐私保证,甚至在(ε,δ)-dp方面也是如此。这一改进归功于f-dp的中心极限定理的使用,它准确地捕捉了每个迭代训练深度学习模型。这在3.2节中介绍,并在4.1节中用数值实验进行说明。
提高了预测精度。利用f-dp提供的更强的隐私保证,我们可以牺牲一定的隐私来提高预测性能。例如,这可以通过适当降低在神经网络的训练过程中添加的噪声量以匹配(ε,δ)-DP方面的目标隐私级别来实现。有关此实用程序改进的开发,请参见第3.2节和第4.2节。
1.1 Related Work
还有很多ff可以用来理解在构图的情况下隐私是如何退化的。沿着这条线的发展包括基本合成定理和高级合成定理[22,24]。在一个开创性的工作中,[32]得到了(ε,δ)-dp的最优合成定理,这实际上是f-dp工作的动机之一[18]。然而,从它们的合成定理[44]来计算隐私界限是困难的。最近,[17]导出了指数机制总体隐私损失的尖锐合成界限。
从不同的角度来看,最近的一个相当大的研究方向是使用概率分布的分歧来放松不同的隐私,以克服(ff)-DP在处理合成方面的弱点[21,11,43,12]。(ff)-DP在处理合成方面的弱点[21,11,43,12]。不幸的是,这些放松要么缺乏通过次抽样放大隐私的论据,要么提出了一个相当复杂的论据,这是使用difi崇拜的理由[8,57]。由于神经网络训练中固有地使用了次抽样,因此将这些松弛直接应用到深度学习的隐私分析中是一种很有意义的做法(difficult)。
为了规避这些与(ffi)-DP及其基于分歧的放松相关的技术上的迷信,阿巴迪等人(Aabadi et al.)[3]发明了一种称为矩会计师的技术来跟踪深度神经网络训练过程中隐私损失的详细信息。使用Moments Accounter,他们的分析显著改进了sgd[14,55,10,53,61]的早期隐私分析,并允许在实际大小的数据集上训练的深度学习的有意义的隐私保证。fi[14,55,10,53,61]通过后续工作,这项技术已经扩展到各种情况[41,48]。相比之下,我们在f-dp框架中对私人深度学习的方法利用了这种新的隐私定义的一些强大的工具,然而提供了更敏锐的隐私分析,正如在第3和第4节中从理论和经验上看到的那样。
为了完整性,我们注意到,已经提出了不同的方法,将隐私考虑纳入深度学习,而没有利用训练深度学习模型的迭代和次采样性质。这项工作包括通过“教师”模型的集合来训练私人模型[47,46],开发带噪声的联合平均算法[42],以及通过神经网络的优化景观的镜头来分析隐私成本[59]。
2 Preliminaries
2.1 f-Differential Privacy
在差分隐私框架(DierentialffPrivacy Framework)中,我们设想除了单个个体之外,攻击者都非常了解数据集其他个体,并且该攻击者试图根据算法的输出来确定该个体是否在该数据集中。粗略地说,如果对很难确定任何人的存在或不存在在数据集中,该算法就被认为是隐私保护的。
非正式地,数据集可以被认为是一个矩阵,它的每一行都包含一个人的数据。如果两个数据集可以通过从另一个数据集中丢弃一个个体来派生,则称两个数据集为相邻数据集。因此,相邻数据集的不同的样本大小只为1。设s0和s1为相邻数据集,ε>0,0 6δ6 1为两个数,用以数据集为输入的MA(随机化)算法表示。
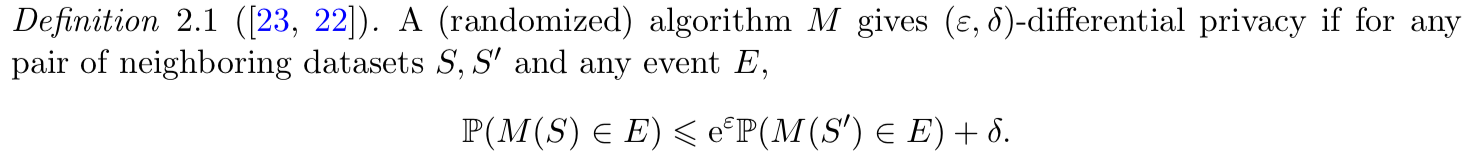
为了实现私密性,算法M必须是随机化的,而Definition 2.1中的两个数据集是确定性的。这种隐私性Definition确保了基于算法的输出,攻击对手在具有有限的(取决于ε,δ有多小)能力来识别任何个体的存在或不存在,而不管是否有任何个体选择加入或退出数据集。
本质上,对手试图用一次平局来区分两个概率分布M(S)和M(S0)。根据这一观察,很自然地将对手的行为解释为检验两个简单的假设:
H 0 : the true dataset is S
versus
H 1 : the true dataset is S 0 .
据我们所知,不同隐私和假设检验之间的联系首先在[58]中指出的,后来在[32,39,9]中得到了发展。
直观地说,如果假设检验问题很难,隐私就会得到很好的保障。根据这一直觉,(fi)-DP的定义实质上是使用分布M(S)和M(S0)的最坏情况似然比来衡量检验这两个简单假设的难度。
有没有更能提供信息的难度的测量方法?在[18]中,作者建议使用类型I错误(当H0为真时错误拒绝H0的概率)和类型II错误(当H1为真时错误接受H0的概率)之间的权衡ff来代替(ε,δ)-DP或基于散度的DP defi数组中的一些隐私参数。
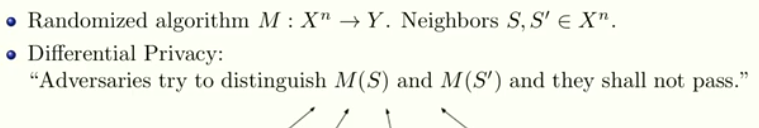

 浙公网安备 33010602011771号
浙公网安备 33010602011771号