20250824 XYD 001 T3

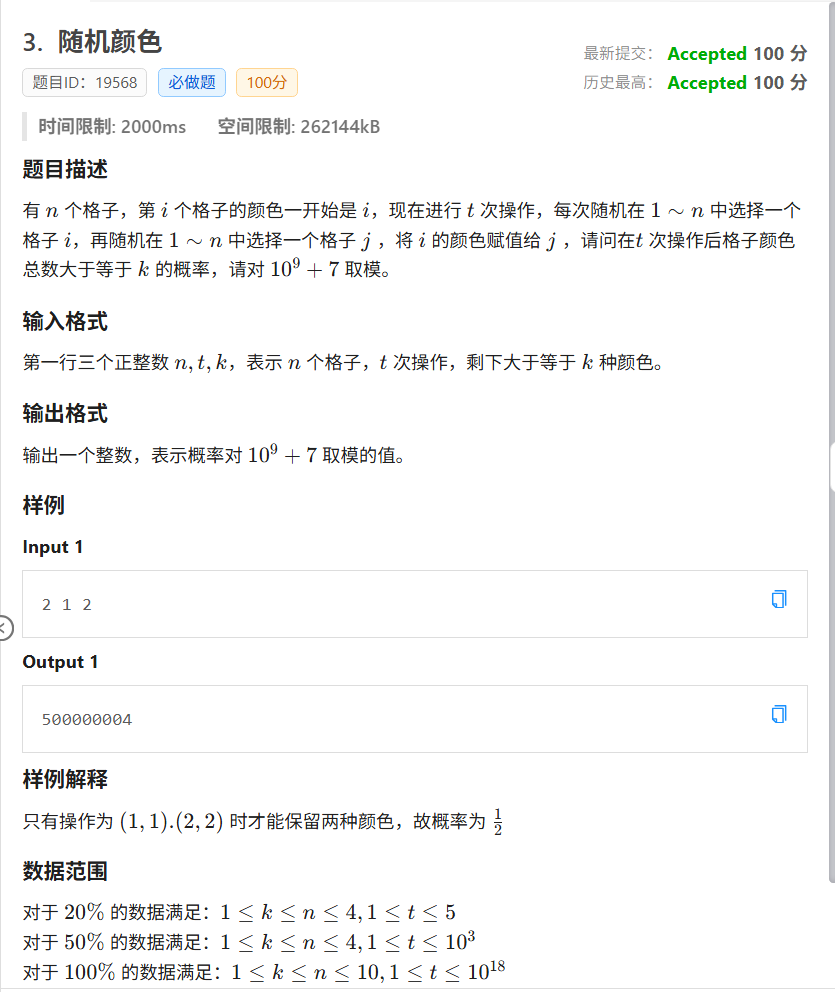
题面

思路

记方案数，考虑 DP。由于 \(t <= 10^{18}\)，联想到矩阵快速幂。

首先不会写 DP，考虑爆搜，可以以当前是第几步，整个 \(a\) 数组是什么样的，作为状态，每次转移枚举两个点。非常劣，考虑优化。先优化状态，因为我们不关注位置，也不关注具体是哪个颜色。所以考虑将每一个颜色的数量作为状态。那么总状态数就是分拆数级别。最后考虑矩阵快速幂即可。

将每个颜色有几个作为状态的正确性：我们发现，对于转移，我们只关注每个颜色有几个，但具体是那个颜色不重要，位置也不重要，对于答案，我们只关注有多少种不同的颜色，所以可以仅将每个颜色有几个作为状态。

Code

#include<bits/stdc++.h>
#define int long long

using namespace std;
using ll = long long;

const int N = 10, F = 45, MOD = 1e9 + 7;

struct Matrix {
	ll n, m, num[F][F];
	Matrix() {
		n = m = 0;
		for (int i = 0; i < 45; i++) {
			for (int j = 0; j < 45; j++) {
				num[i][j] = 0;
			}
		}
		return ; 
	}
	Matrix operator * (const Matrix x) {
		Matrix y;
		y.n = n, y.m = x.m;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= x.m; j++) {
				for (int k = 1; k <= m; k++) {
					y.num[i][j] = (y.num[i][j] + num[i][k] * x.num[k][j] % MOD) % MOD;
				}
			}
		}
		return y;
	} 
};

ll ans;
ll n, t, k, f;
int flag[F];
vector<int> cv[F], v; 
map<vector<int>, int> m;
Matrix a, dp;

ll Pow(ll a, ll b) {
	ll ans = 1;
	for (; b; b >>= 1ll, a = a * a % MOD) {
		if (b & 1ll) {
			ans = ans * a % MOD;
		}
	}
	return ans;
}

void DFS(int sum, int lst) {
	if (sum == 0) {
		f++;
		m[v] = f;
		cv[f] = v;
		flag[f] = v.size() >= k;
		return ;
	}
	for (int i = 1; i <= min(lst, sum); i++) {
		v.push_back(i);
		DFS(sum - i, i);
		v.pop_back();
	}
	return ;
}

void Init_I(Matrix &x) {
	x.n = x.m = f;
	for (int i = 1; i <= x.n; i++) {
		x.num[i][i] = 1;
	}
	return ;
}

void Init_DP(Matrix &x) {
	x.n = 1, x.m = f;
	x.num[1][1] = 1;
	return ;
}

void Build(Matrix &x) {
	x.n = x.m = f;
	for (int i = 1; i <= f; i++) {
		for (int j = 0; j < cv[i].size(); j++) {
			for (int k = 0; k < cv[i].size(); k++) {
				vector<int> v = cv[i];
				v[j]--, v[k]++;
				sort(v.begin(), v.end(), greater<int>());
				for (; v.back() == 0; v.pop_back()) ;
				x.num[i][m[v]] = (x.num[i][m[v]] + (ll) cv[i][j] * cv[i][k] % MOD * Pow(n * n % MOD, MOD - 2) % MOD) % MOD;
			}
		}
	}
	return ;
}

Matrix Pow(Matrix a, ll b) {
	Matrix ans;
	Init_I(ans);
	for (; b; b >>= 1ll, a = a * a) {
		if (b & 1ll) {
			ans = ans * a;
		}
	}
	return ans;
}

 main() {
	cin >> n >> t >> k; 
	DFS(n, n);
	Build(a);
	Init_DP(dp);
	a = Pow(a, t);
	dp = dp * a;
	for (int i = 1; i <= f; i++) {
		ans = (ans + flag[i] * dp.num[1][i] % MOD) % MOD;
	}
	cout << ans;
	return 0;
}

总结

分拆数。

缩减状态。