字符串问题的歪门奇宝：进制哈希

江湖中，剑客以快制胜，而算法竞赛里，字符串哈希（String Hashing）便是那柄出招如电的快剑。

各种字符串问题纷乱复杂，各种字符串算法招式繁复，需苦练内功心法。但字符串哈希算法却只凭一招：将字符串化作数字，以数论为刃，至简之道斩尽来犯之敌。

但此招并非无懈可击。若遇精心构造的数据，它可能一剑刺空，露出破绽。然而，在绝大多数情况，它仍是侠客们最趁手的兵器——七分准，三分险，却快得让人无从招架。

何为进制哈希？

哈希是复杂对象到较小整数的映射，而进制版本的字符串哈希是一种很有趣的哈希方式。他把字符串转化为一个b进制的数值。

例如，字符串 "ab"：

  • 若设 u=1, v=2，取 base=131（进制基数），则其哈希值为：

    \[H('uv') = 1 \times 131^1 + 2 \times 131^0 = 133 \]

既然是将字符视为数，那每个字符需要一个值，同时还需要一个进制大小。

考虑字符集（Character Set），一般就使用字符的编码即可（如 ascii 或 unicode），简单起见本文只考虑小写字母集：a-z（26个字符），对应1-26

注：为什么不使用0-25？因为把 0 放入编码，会导致出现"a"和"aa"相等，"aaabcd"和"aaaaabcd"相等的情况，太容易构造冲突。为了应对构造数据，不如直接使用 ascii 本身，或者至少让a-z（26个字符），对应1-26。

考虑基数（Base）的选择，基数显然至少大于字符集大小。若用a-z，26字符去除 0，需要 27进制，实际上也可以更大，常用质数基数：131、13331 等。

随着字符串长度增加，这个数迅速就变得非常大，所以要再对某个大质数取模，便得到最终的编码。

查询子串哈希

字符串哈希之所以是"快剑"，因为它有一个奇妙的性质：它能通过前缀哈希（Prefix Hash），在 O(1) 时间内斩出任意子串的哈希值。

选定编码和基数后，我们处理出a[i]：存储前 s[0..i] 的哈希值，显然有秦九韶算法：a[i] = a[i-1] * base + d;

现在我们要计算子串s[l..r]的哈希，其原理如同在进制数中取数：

  1. 将前缀哈希a[r]视为大数。
  2. 减去a[l-1]向左位移(r-l+1)位的干扰（通过乘p[r-l+1]实现，p为基数的幂次）

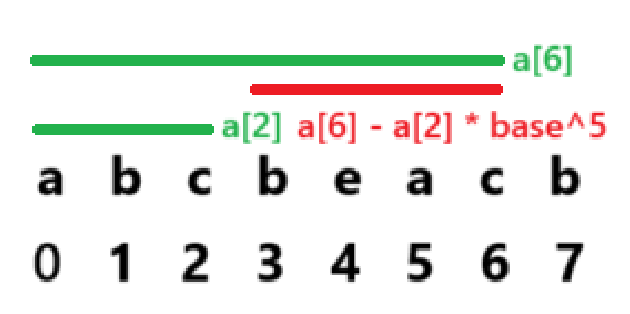
image

// 为了简单和效率，直接选用 unsigned long long，模数等价于2^64，称为自然溢出。
class hashstr {
    using u64 = unsigned long long;

    int n;
    u64 mod;
    vector<u64> a, p;

    const static int base = 131;
public:
    hashstr(const string &s, u64 mod = 0): n(s.size()), a(n), p(n+1) {
        u64 x = 0;
        for (int i = 0; i < n; ++i) {
            int d = s[i]; // ASCII
            a[i] = x * base + d;
        }

        p[0] = 1;
        for (int i = 1; i <= n; ++i) p[i] = p[i-1] * base;
    }

    u64 hash(int l, int r) {
        return a[r] - (l ? a[l-1]*p[r-l+1] : 0);
    }
};

// 示例：已处理"abcd"，计算"bcd"的哈希
hash(1,3) = a[3] - a[0]*p[3] 
           = (a*B^3 + b*B^2 + c*B^1 + d*B^0) - a*B^3
           = b*B^2 + c*B^1 + d*B^0 = hash(1,3)
操作 时间复杂度 空间复杂度
预处理 O(n) O(n)
子串查询 O(1) -

这就意味着，给定一个或多个字符串，我们可以瞬间判断出一个字符串的某子串和另一字符串的某子串是否相等，无需任何比较！

「赖皮」之道：四两拨千斤的解题哲学

在算法江湖中，字符串哈希被戏称为「赖皮算法」——它不似正统数据结构那般严谨，却总能用巧劲化解难题。其精髓在于：将字符串问题暴力转化为数字问题。

1 回文判定（Palindrome Detection）

正统解法：Manacher算法（O(n)）

哈希赖皮法：

  1. 准备原字符串和原字符串的反转的前缀进制哈希。正向计算前缀哈希，反向计算后缀哈希
  2. 比较子串[l,r]的正向哈希与反向哈希

2 字符串匹配（Pattern Matching）

正统解法：KMP（O(n+m)）

哈希赖皮法：

  1. 预处理模式串哈希H(pattern)
  2. 滑动窗口直接计算文本串所有长度为m的子串哈希

3 最长重复子串（Longest Repeated Substring）

正统解法：后缀数组（O(nlogn)）

哈希赖皮法：

  1. 二分可能的最大长度L
  2. 用哈希存储所有长度为L的子串，检查碰撞

4 最长公共子串（Longest Common Substring）

正统解法：后缀自动机（O(n)）

哈希赖皮法：

  1. 二分可能的最大长度L
  2. 分别计算两个字符串所有长度为L的子串哈希集
  3. 求哈希集合的交集

5 循环同构判定（Cyclic Isomorphism）

正统解法：最小表示法（O(n)）

哈希赖皮法：

  1. 构造原字符串的哈希环S = S + S
  2. 比较所有可能旋转位置的子串哈希

江湖箴言：
"哈希算法七分险，快剑无影胜有影。
若遇生死决赛场，双哈希出保太平。"

处理哈希碰撞问题

选择模数

飞刀轻快但易折，重剑无锋却难精，双剑合璧则近乎无敌。不同的场景需用不同的方法。

对于 \(n\) 个字符串和模数 \(p\)，生日悖论给出的冲突概率：

\[P \approx 1 - e^{-\frac{n(n-1)}{2p}} \]

  1. 小质数模数（如 1e9+7）需显式取模，常数较大，且碰撞风险高：若数据量超过 \(\sqrt{p}\)（约3e4），生日悖论导致碰撞概率显著上升

    • 例如：用p=1e9+7处理1e5个字符串时，碰撞概率约5%
    • 适用场景：
      • 小规模数据（n≤1e4）
      • 需严格控制哈希值范围的场景

  2. 大质数模数（如 1e18+3）的碰撞概率极低：值域巨大，可安全处理 1e6 级数据。不过计算的代价增加。自己选取大质数，更拥有抗构造性，难以针对随机大质数构造碰撞数据。

  3. 自然溢出（\(2^{64}\)）飞刀迅捷，却怕预判。利用 CPU 和无符号整数自动溢出，无显式取模操作，非常高效。但模数固定为 \(2^{64}\)，数字虽大，但已经确定。攻击者容易构造冲突数据。如 Thue-Morse 序列可导致大规模碰撞

    • 适用场景：
      • 非对抗性环境（如企业内部数据处理）
      • 时间极其敏感的竞赛场景

  4. 双哈希（Dual Hash）子母鸳鸯，万无一失。同时使用两个不同基数和模数的哈希系统，例如：(base1=131, mod1=1e9+7) + (base2=13331, mod2=1e18+3)

    • 优势：
      • 需两个哈希值同时碰撞才算冲突，概率非常非常非常低
      • 即使攻击者破解一组参数，另一组仍可保障安全
    • 代价：
      • 空间和时间翻倍
场景 推荐策略 理由
竞赛常规题 自然溢出 代码简洁，跑得快
对抗性构造数据 双哈希 绝对安全
超大字符集（如Unicode） 大质数+双哈希 避免基数不足导致冲突
内存敏感环境 单大质数 平衡安全与空间

选择基数

基数选择也对碰撞概率有影响。首先基数应该至少和字符集一样大，其次优质基数应满足三大特征：

  1. 与模数互质：若模数为质数，则基数只需非其倍数。互质可以避免出现周期性重复，最大化利用值域空间（如base=2时哈希值奇偶性固定）

  2. 远离模数的二次剩余：防止出现 \(base^k \equiv 1 \ (\text{mod} \ p)\) 的短周期。例如base=10与p=1e9+7的组合周期仅为 \(p-1\)，实际效果差

  3. 高熵分布：推荐使用不规则大质数

优质基数可将冲突率再降一个数量级：

// 此版本可以指定模数和基数，间接支持了多哈希
template <int BASE = 13331, unsigned long long MOD = 0>
class HashStr {
    using u64 = unsigned long long;
    int n;
    vector<u64> a, p;

public:
    HashStr(const string &s) : n(s.size()), a(n), p(n + 1) {
        u64 x = 0;
        for (int i = 0; i < n; ++i) {
            int d = s[i]; // 使用ASCII码，支持更广字符集
            if constexpr (MOD)
                a[i] = (x * BASE + d) % MOD;
            else
                a[i] = x * BASE + d;
            x = a[i];
        }
        p[0] = 1;
        for (int i = 1; i <= n; ++i) {
            if constexpr (MOD)
                p[i] = p[i - 1] * BASE % MOD;
            else
                p[i] = p[i - 1] * BASE;
        }
    }

    u64 hash(int l, int r) const {
        if (l) {
            if constexpr (MOD)
                return (a[r] - (a[l - 1] * p[r - l + 1]) % MOD + MOD) % MOD;
            else
                return a[r] - a[l - 1] * p[r - l + 1];
        }
        return a[r];
    }
};

（醒木一拍）

《哈希江湖志》

进制为基化剑芒，
子串快剑破风霜。
小质易折如薄柳，
大模稳坐似山冈。

自然溢出飞刀迅，
双哈希出鬼神慌。
莫道此招多取巧，
九成胜算即称王！

（醒木再拍）

posted @ 2025-03-26 00:26  Ofnoname  阅读(550)  评论(0)    收藏  举报