CF2164F2 奇怪做法
又难写又慢的做法。
按照值从小往大填,显然能填 \(1\) 的一定是当前树上,子树中没有别的 \(0\) 的 \(a_u=0\) 的 \(u\),将其加入备选队列 \(q\)。每次取出 \(u\),对子树内所有未删除的点 \(v\) 的 \(a_v\to a_v-1\)。用一个重构图 \(G\) 来描述限制,如果产生新的 \(a_v=0\),找到这些点中所有子树中没有别的 \(0\) 的位置,在 \(G\) 上向它们连边并加入队列;如果并没有,那么找到祖先中首个 \(0\) 向它连边。如果此时它的子树中没有别的 \(0\) 那么就加入队列。
如此可以构造图 \(G\),此时排列 \(p\) 合法当且仅当 \(p\) 是一个 \(G\) 的拓扑序。\(G\) 是一张极为特殊的 DAG,满足 \(1\) 在拓扑序的位置固定。对 \(G\) 进行:叠合杏仁,缩二度点构成的链这两种操作后,最终 \(G\) 的形态是:取出所有可达 \(1\) 的点,子图是一张以 \(1\) 为根的内向树;取出所有 \(1\) 可达的点,子图是一张以 \(1\) 为根的外向树;使用队列维护简化 \(G\) 的流程,最终贡献就与树的拓扑序求法类似。
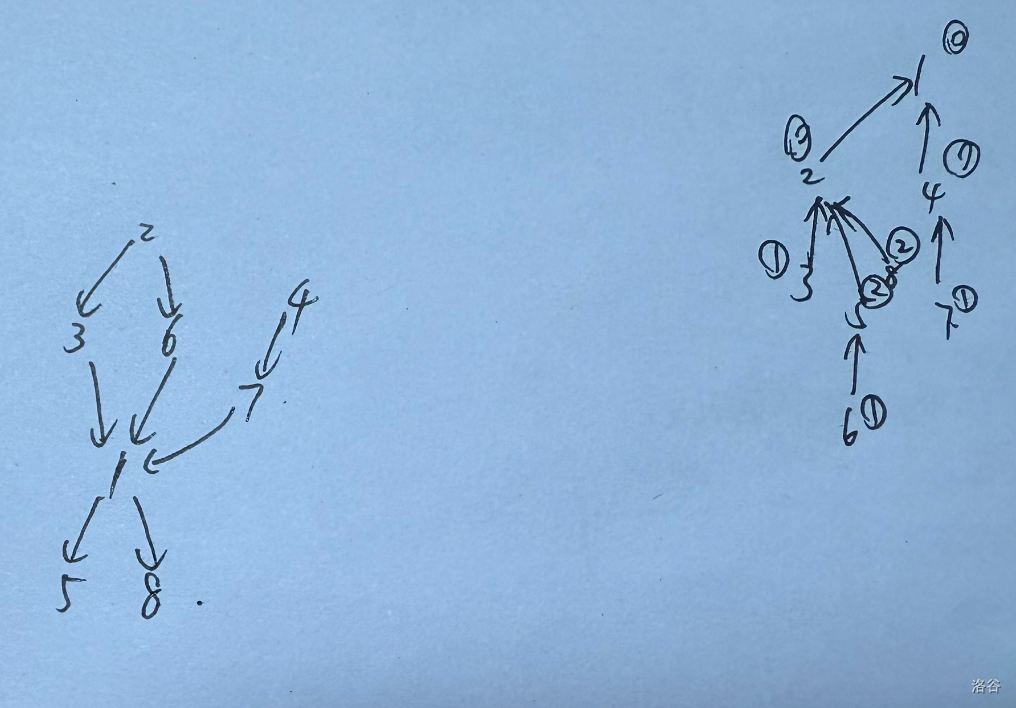
对拍时随便造的一组,可以对着理解一下。
现在 \(\mathcal O(n^2)\) 做法随便写。F1 提交记录。
在构造 \(G\) 的过程中使用树剖线段树维护区间最小值信息,每次取 \(\text{dfn}\) 最大的,以及在树链上倍增即可降低复杂度。取出来一个之后就把所有祖先 ban 掉,可以维护权值 \(b_i\)。线段树维护的信息为 \(\min(b_i)\) 以及所有 \(\min(b_i)\) 中的 \(\min(a_i)\),这样就可以合并了。线段树二分首先要求 \(\min(b_i)=0\),再要求这里面的 \(\min(a_i)=0\)。
时间复杂度 \(\mathcal O(n\log^2n)\),如果使用全局平衡二叉树,时间复杂度 \(\mathcal O(n\log n)\)。F2 提交记录。
code:
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define uint unsigned
#define pb push_back
#define mkp make_pair
#define fi first
#define se second
#define inf 1000000000
#define infll 1000000000000000000ll
#define pii pair<int,int>
#define rep(i,a,b,c) for(int i=(a);i<=(b);i+=(c))
#define per(i,a,b,c) for(int i=(a);i>=(b);i-=(c))
#define F(i,a,b) for(int i=a,i##end=b;i<=i##end;i++)
#define dF(i,a,b) for(int i=a,i##end=b;i>=i##end;i--)
#define eb emplace_back
#define SZ(x) ((int)x.size())
#define all(x) x.begin(),x.end()
using namespace std;
bool ST;
inline int lowbit(int x){ return x&(-x); }
template<typename T>inline void chkmax(T &x,const T &y){ x=std::max(x,y); }
template<typename T>inline void chkmin(T &x,const T &y){ x=std::min(x,y); }
const int mod=998244353,maxn=500005;
inline int qpow(int x,ll y){ int res=1; for(;y;y>>=1,x=1ll*x*x%mod)if(y&1)res=1ll*res*x%mod; return res; }
inline void inc(int &x,const int y){ x=(x+y>=mod)?(x+y-mod):(x+y); }
inline void dec(int &x,const int y){ x=(x>=y)?(x-y):(x+mod-y); }
inline int add(const int x,const int y){ return (x+y>=mod)?(x+y-mod):(x+y); }
inline int sub(const int x,const int y){ return (x>=y)?(x-y):(x+mod-y); }
int fac[maxn],ifac[maxn];
void init(const int N){
fac[0]=ifac[0]=1;
F(i,1,N)fac[i]=1ll*fac[i-1]*i%mod;
ifac[N]=qpow(fac[N],mod-2);
dF(i,N-1,1)ifac[i]=1ll*ifac[i+1]*(i+1)%mod;
}
vector<int>g[maxn],h[maxn],e[maxn];
int n,fa[maxn],a[maxn],num[maxn],dfn[maxn],rev[maxn],tim,siz[maxn],son[maxn],top[maxn];
void dfs(int u){
siz[u]=1,son[u]=0;
for(int v:g[u]){
dfs(v),siz[u]+=siz[v];
if(siz[v]>siz[son[u]])son[u]=v;
}
}
void dfs_(int u,int t){
top[u]=t,rev[dfn[u]=++tim]=u;
if(!son[u])return;
dfs_(son[u],t);
for(int v:g[u])if(v^son[u])dfs_(v,v);
}
namespace Sub{
vector<int>E[maxn];
bool vis[maxn];
void dfs1(int u){
if(vis[u])return;
vis[u]=1;
for(int v:E[u])dfs1(v);
}
set<int>sin[maxn],sout[maxn];
int siz[maxn],in[maxn],out[maxn],del[maxn];
pii dfs2(int u){
int sm=siz[u],pr=1;
for(int v:sout[u]){
auto[x,y]=dfs2(v);
sm+=y,pr=1ll*pr*x%mod;
}
pr=1ll*pr*fac[sm-siz[u]]%mod*ifac[sm]%mod;
return mkp(pr,sm);
}
#define H(u,v) (1ll*(n+1)*u+v)
int sol(){
F(i,1,n)vis[i]=in[i]=out[i]=del[i]=0,sin[i].clear(),sout[i].clear(),siz[i]=1;
dfs1(1);
vector<int>V;
F(i,1,n)if(vis[i])V.push_back(i);
for(int i:V)for(int j:E[i])if(vis[j])++in[j],++out[i],sin[j].insert(i),sout[i].insert(j);
queue<pii>st,st1;
unordered_map<ll,vector<int>>mp;
auto upd=[&](int x){
if(del[x])return;
in[x]=SZ(sin[x]),out[x]=SZ(sout[x]);
if(in[x]==1&&out[x]==1){
int u=*sin[x].begin(),v=*sout[x].begin();
mp[H(u,v)].push_back(x);
if(SZ(mp[H(u,v)])>1)st.push(mkp(u,v));
if(in[u]==1&&out[u]==1)st1.push(mkp(u,x));
if(in[v]==1&&out[v]==1)st1.push(mkp(x,v));
}
};
for(int i:V)upd(i);
int ans=1;
while(!st.empty()||!st1.empty()){
if(!st1.empty()){
const auto[u,v]=st1.front();st1.pop();
if(del[u]||del[v])continue;
const int x=*sout[v].begin();
sin[x].erase(v),sin[x].insert(u);
del[v]=1,sout[u]=sout[v],siz[u]+=siz[v],upd(u),upd(x);
continue;
}
const auto[u,v]=st.front();st.pop();
if(del[u]||del[v]||SZ(mp[H(u,v)])<=1)continue;
const vector<int>vec=mp[H(u,v)];
mp[H(u,v)]={vec[0]};
for(int x:vec)ans=1ll*ans*ifac[siz[x]]%mod;
F(i,1,SZ(vec)-1)del[vec[i]]=1,siz[vec[0]]+=siz[vec[i]],sout[u].erase(vec[i]),sin[v].erase(vec[i]);
ans=1ll*ans*fac[siz[vec[0]]]%mod;
upd(u),upd(v);
}
auto[A,B]=dfs2(1);
ans=1ll*ans*A%mod*fac[B]%mod;
return ans;
}
}
namespace seg{
#define ls (o<<1)
#define rs (o<<1|1)
int ban[maxn<<2],t[maxn<<2],tag[maxn<<2],btag[maxn<<2],tr[maxn<<2];
inline void init(){ F(i,1,n<<2)ban[i]=t[i]=tag[i]=btag[i]=tr[i]=0; }
inline void mt(int o,int val){ tag[o]+=val,t[o]+=val,tr[o]+=val; }
inline void bt(int o,int val){ ban[o]+=val,btag[o]+=val; }
inline void pd(int o){
if(tag[o])mt(ls,tag[o]),mt(rs,tag[o]),tag[o]=0;
if(btag[o])bt(ls,btag[o]),bt(rs,btag[o]),btag[o]=0;
}
inline void up(int o){
pd(o);
ban[o]=min(ban[ls],ban[rs]),tr[o]=min(tr[ls],tr[rs]);
if(ban[ls]<ban[rs])t[o]=t[ls];
else if(ban[ls]>ban[rs])t[o]=t[rs];
else t[o]=min(t[ls],t[rs]);
}
inline void update(int o,int l,int r,int ql,int qr,int val){
if(ql>qr)return;
if(ql<=l&&qr>=r)return mt(o,val),void();
int mid=(l+r)>>1;pd(o);
if(ql<=mid)update(ls,l,mid,ql,qr,val);
if(qr>mid)update(rs,mid+1,r,ql,qr,val);
up(o);
}
inline void addban(int o,int l,int r,int ql,int qr,int val){
if(ql>qr)return;
if(ql<=l&&qr>=r)return bt(o,val),void();
int mid=(l+r)>>1;pd(o);
if(ql<=mid)addban(ls,l,mid,ql,qr,val);
if(qr>mid)addban(rs,mid+1,r,ql,qr,val);
up(o);
}
inline int find(int o,int l,int r,int lim){
if(lim<l||t[o]>0||ban[o]>0)return -1;
if(l==r)return l;
int mid=(l+r)>>1;pd(o);
if(mid<lim){
int res=find(rs,mid+1,r,lim);
if(res>0)return res;
}
return find(ls,l,mid,lim);
}
inline int find1(int o,int l,int r,int ql,int qr){
if(tr[o]>0)return -1;
if(ql<=l&&qr>=r){
while(l<r){
int mid=(l+r)>>1;pd(o);
if(tr[rs]==0)l=mid+1,o=rs;
else r=mid,o=ls;
}
return l;
}
int mid=(l+r)>>1;pd(o);
if(qr>mid){
int res=find1(rs,mid+1,r,ql,qr);
if(res>0)return res;
}
if(ql<=mid)return find1(ls,l,mid,ql,qr);
return -1;
}
inline int qban(int pos){
int l=1,r=n,o=1;
while(l<r){
int mid=(l+r)>>1;pd(o);
if(pos<=mid)r=mid,o=ls;else l=mid+1,o=rs;
}
return ban[o];
}
#undef ls
#undef rs
}
void solve(){
cin>>n;
F(i,0,n)g[i].clear(),h[i].clear(),e[i].clear();
F(i,2,n)cin>>fa[i],g[fa[i]].push_back(i);
dfs(1),tim=0,dfs_(1,1),seg::init();
F(i,1,n)cin>>a[i],num[i]=(a[i]==0);
F(i,1,n)seg::update(1,1,n,dfn[i],dfn[i],a[i]);
auto linkban=[&](int u,int val){
for(;u;u=fa[top[u]])seg::addban(1,1,n,dfn[top[u]],dfn[u],val);
};
dF(i,n,2)num[fa[i]]+=num[i];
queue<int>q;
vector<int>inq(n+1,0);
F(i,1,n)if(a[i]==0&&num[i]==1)q.push(i),inq[i]=1,linkban(i,1);
while(!q.empty()){
const int u=q.front();q.pop();
seg::update(1,1,n,dfn[u],dfn[u],inf),linkban(u,-1);
seg::update(1,1,n,dfn[u]+1,dfn[u]+siz[u]-1,-1);
vector<int>vec;
int lst=dfn[u]+siz[u];
while(1){
if(lst<=1)break;
int v=seg::find(1,1,n,lst-1);
if(v==-1||v<=dfn[u])break;
linkban(rev[v],1),lst=v,vec.push_back(rev[v]);
}
if(!vec.empty()){
for(int v:vec)q.push(v),inq[v]=1,h[u].push_back(v);
} else{
int to=0;
for(int v=fa[u];v;v=fa[top[v]]){
int res=seg::find1(1,1,n,dfn[top[v]],dfn[v]);
if(res>0){
to=rev[res];
break;
}
}
if(!to)continue;
h[u].push_back(to);
if(!inq[to]&&seg::qban(dfn[to])==0)q.push(to),inq[to]=1,linkban(to,1);
}
}
F(u,1,n)for(int v:h[u])e[v].push_back(u);
F(u,1,n)Sub::E[u]=h[u];
int ans=Sub::sol();
F(u,1,n)Sub::E[u]=e[u];
ans=1ll*ans*Sub::sol()%mod;
cout<<ans<<'\n';
}
bool ED;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int wzq=1; cin>>wzq,init(maxn-3);
F(____,1,wzq)solve();
cerr<<"time used: "<<(double)clock()/CLOCKS_PER_SEC<<endl;
cerr<<"memory used: "<<abs(&ST-&ED)/1024.0/1024.0<<" MB"<<endl;
}
// g++ CF2164F1.cpp -o a -std=c++14 -O2
posted on 2025-11-09 12:36 nullptr_qwq 阅读(50) 评论(1) 收藏 举报

 浙公网安备 33010602011771号
浙公网安备 33010602011771号