第四范式笔试

第一题





Example:

Consider the following matrix:

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.
Given target = 20, return false.

// T(n) = O(m+n)
// S(n) = O(1)
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size();
        if (m == 0) return false;
        int n = matrix[0].size();

        int i = 0, j = n - 1;
        while (i < m && j >= 0) {
            if (matrix[i][j] == target)
                return true;
            else if (matrix[i][j] > target) {
                j--;
            } else 
                i++;
        }
        return false;
    }
};

第二题

二部图概念



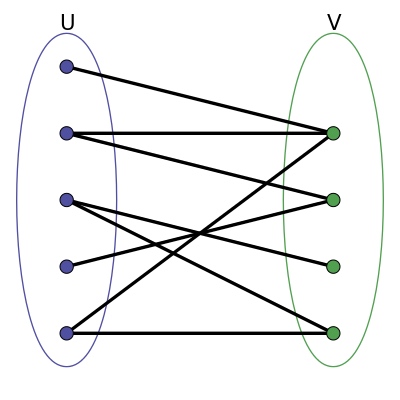
二分图又称双分图、二部图、偶图，指顶点可以分成两个不相交的集 U 和 V, U, V 皆为独立集（independent sets），使得在同一个集内的顶点不相邻（没有共同边）的图。

二分图又称作二部图，是图论中的一种特殊模型。 设 G=(V,E) 是一个无向图，如果顶点 V 可分割为两个互不相交的子集 (U, V)，并且图中的每条边 (i, j) 所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集 \(i \in U\), \(j \in V\)，则称图 G 为一个二分图。

可以将 U 和 V 当做着色图

U 中所有节点为蓝色, V 中所有节点着绿色，每条边的两个端点的颜色不同，符合图着色问题的要求。相反，用这样的着色方式对非二分图是行不通的，根据三角关系：其中一个顶点着蓝色并且另一个着绿色后，三角形的第三个顶点与上述具有两个颜色的顶点相连，无法再对其着蓝色或绿色(即非二分图, 存在一个顶点既属于 U, 又属于 V)。

解题思路

根据二分图的特性，一条边上的两个点，肯定是属于不同的组。如果它们出现在同一个组中，肯定就不是二分图了。

怎么判断，一条边上的两个点，分属于不同的组呢？

我们需要遍历图，如果找到一条边，两个节点，都在同一组，则不是二分图；如果图遍历完成之后，没有找到这样的边，则是二分图。我们在遍历的过程中，我们需要区分，一条边的两个节点分属于不同的组，这里我们用到了染色法。

核心思想如下：

从某一个点开始，将这个节点染色为白色，并且开始广度优先遍历，找到与其相邻的节点，如果是二分图，相邻节点的颜色都应该不同。如果是黑色，则不变；如果是无色，则染成黑色；如果是白色，也就是同色，程序退出。当图遍历完毕时，没有相邻节点同色的，则是二分图，标记为白色和黑色的两组就是一个划分。



input:
5 6
1 2
2 3
3 4
4 1
4 5
5 2

output:
Yes

input:
5 4
1 2
2 3
3 1  
4 5

output:
No
解释: 有三角形存在.

#include <queue>
#include <iostream>
using namespace std;

bool isBipartiteGraph(vector<vector<int>> &mygraph,
                      vector<int> &color, int vertex) {
    int n = mygraph.size();
    queue<int> vertexes;
    vertexes.push(vertex);
    // 对于还未被染色 vertex, 设置为 1 或者为 0 都可以, 这是由于该 vertex 已经在第二个连通图中
    // 如果 vertex 还在之前的连通图中的话,
    // 那么该 vertex 一定会被遍历, 所以该 vertex 不在之前的连通图中.
    color[vertex] = 1;
    while(!vertexes.empty()) {
        int from = vertexes.front();
        vertexes.pop();
        for(int to = 0; to < n; to++) {
            if(mygraph[from][to]) {
                if (color[to] == -1) {
                    vertexes.push(to);
                    color[to] = !color[from]; //染成不同的颜色, 使用!求反, 很骚气
                } else if (color[from] == color[to]) {
                    //颜色有相同，则不是二分图
                    return false;
                }
            }
        }
    }
    return true;
}

int main() {
    int num_vertex, num_edge;
    cin >> num_vertex >> num_edge;
    vector<vector<int>> adjMatrix(num_vertex, vector<int>(num_vertex));
    vector<int> color(num_vertex, -1);
    int u, v;
    for(int i = 0; i < num_edge; i++) {
        cin >> u >> v;
        u -= 1;
        v -= 1;
        adjMatrix[u][v] = adjMatrix[v][u] = 1;
    }

    bool isBipartite = true;
    for(int i = 0; i < num_vertex; i++)
        // 如果该节点还未被遍历
        if(color[i] == -1 ) {
            if (!isBipartiteGraph(adjMatrix, color, i)) {
                isBipartite = false;
                break;
            }
        }

    if (isBipartite) cout << "Yes" <<endl;
    else cout << "No" <<endl;

    return 0;
}