漂亮数组

分治主题

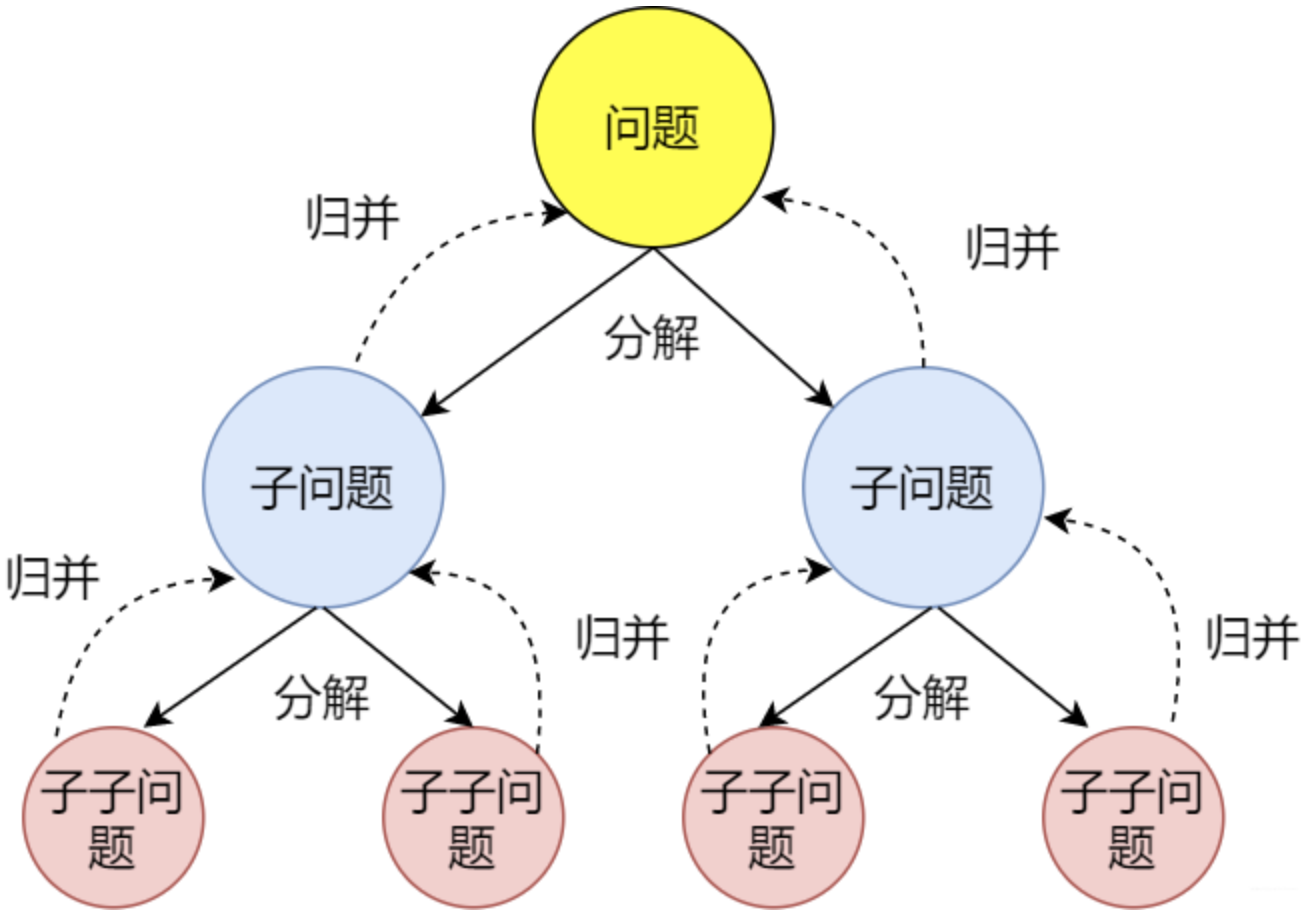
最典型的是快速排序算法和归并排序算法

1. 快速排序算法是先划分，再递归快速排序；
2. 归并排序算法是先递归归并排序，再合并；

932. 漂亮数组

对于某些固定的 N，如果数组 A 是整数 1, 2, ..., N 组成的排列，使得：

对于每个 i < j，都不存在 k 满足 i < k < j 使得 A[k] * 2 = A[i] + A[j]。

那么数组 A 是漂亮数组。

给定 N，返回任意漂亮数组 A（保证存在一个）。

示例 1：

输入：4
输出：[2,1,4,3]

示例 2：

输入：5
输出：[3,1,2,5,4]

提示：

1 <= N <= 1000

分析

数组A包含数字1、2、3 ... N

对于任意i < k < j，A[k] * 2 ≠ A[i] + A[j]

1. 看这个式子首先联想的是 奇数 + 偶数 ≠ 数字 * 2

   那么奇数放左边，偶数放右边，中间任意数，这样的三元组肯定符合条件，例如 N为5，[1, 3, 5, 2, 4]

2. 现在考虑如何让奇数之间满足条件，偶数之间满足条件

   这步思维有点跳跃，如何拼凑一个满足条件的奇数/偶数序列呢？

   直接求，想不出来，假设我现在有一个大小为N的漂亮数组呢？

   线程变换不影响等式的关系

   奇变换拼凑奇数序列，1，2，3， ...，i ——》1，3，5，...，2 * i - 1

   偶变换拼凑偶数序列，1，2，3， ...，i ——》2，4，6，...，2 * i

3. 假设ba(n)生成大小为n为的漂亮数组，n为\(2^i\)，先求出大小为\(\frac{n}{2}\)的漂亮数组，左边做奇变换（2*i-1），右边做偶变换（2*i），就能生成大小为n的漂亮数组，即ba(2n)再顺着捋一遍

   [1, 5, 3, 7,| 2, 6, 4, 8]《——[1, 3, 2, 4]

   [1, 3,| 2, 4]《——[1, 2]

   [1,| 2]《——[1]

   |表示左边界和右边界的分界线

4. 大小为\(2^i\)解决了，但给定n不会每次恰好都为幂次方的数，将n拆分为 \(\frac{n+1}{2}\)和\(\frac{n}{2}\)递归求漂亮数组

   当n为偶数时，\(\frac{n+1}{2}\)和\(\frac{n}{2}\)相等；

   当n为奇数时，\(\frac{n+1}{2}\)比\(\frac{n}{2}\)大1；

代码

// 逻辑版，无优化
class Solution {
    public int[] beautifulArray(int N) {
        if (N == 1) {
            return new int[]{1};
        }
        int[] l_base = beautifulArray((N + 1) / 2);
        int[] r_base = beautifulArray(N / 2);
        int[] res = new int[N];
      
        for(int i = 0; i < (N + 1) / 2; i++) {
            res[i] = 2 * l_base[i] - 1;
        }
        for(int i = (N + 1) / 2, j = 0; i < res.length; i++, j++) {
            res[i] = 2 * r_base[j];
        }
        return res;
    }
}

// 备忘录方法优化
class Solution {
    Map<Integer, int[]> memo = new HashMap<>();

    public int[] beautifulArray(int N) {
        if(memo.containsKey(N)) {
            return memo.get(N);
        }
        if (N == 1) {
            memo.put(1, new int[]{1});
            return memo.get(1);
        }
        int l_mid = (N + 1) / 2;
        int r_mid = N / 2;
        int[] l_base = memo.getOrDefault(l_mid, beautifulArray(l_mid));
        int[] r_base = memo.getOrDefault(r_mid, beautifulArray(r_mid));
        int[] res = new int[N];
        for(int i = 0; i < l_mid; i++) {
            res[i] = 2 * l_base[i] - 1;
        }
        for(int i = l_mid, j = 0; i < res.length; i++, j++) {
            res[i] = 2 * r_base[j];
        }
        memo.put(N, res);
        return res;
    }
}

思考

1. 当n≠\(2^i\)时，将n拆分为 \(\frac{n+1}{2}\)和\(\frac{n}{2}\)递归求漂亮数组，我求后\(\frac{n}{2}\)个数，直接基于 \(\frac{n+1}{2}\)的漂亮数组求偶变换不可以嘛？

2. 相似题：构造一个大小为N的数组，要求对于任意每个 i <k < j，arr[k] * 2 ≠ arr[i] + arr[j]，对比下与漂亮数组的不同，以及思考1的解决方式是否可行？

引用

1. 漂亮数组官网题解；

2. 左神美团算法题1讲解；