数论
前言
简单的这里就不放了,放几个比较有意思/新学的。
数学好困难QwQ
Ⅰ.整除/互质性质
若 \(a\) 与 \(b\) 互质,则 \(a+b\) 与 \(ab\) 互质.

Ⅱ. gcd/lcm神奇性质
- \(\gcd(F(a),F(b))=F(\gcd(a,b))\),\(F(n)\) 为斐波那契数列
我们熟知以下 \(A,B,C\) 等性质
\(A.F(n+m)=F(n)F(m+1)+F(n-1)F(m)\)
\(B.\sum\limits_{i=1}^{n}F(i)=F(n+2)-F(2)\)
\(C.\sum\limits_{i=1}^{n}F^2(i)=F(n)F(n+1)\)
即可证 \(\gcd(F(a),F(b))=\gcd(F(a-b),F(b))\),由 \(\gcd\) 性质可证。 - \(\gcd(a,b)=1,\)则\(\gcd(a^m,b^n)=1\)
- \(\gcd(a^n-1,a^m-1)=a^{\gcd(n,m)}-1\)
- \(\gcd(a^n-b^n,a^m-b^m)=a^{\gcd(n,m)}-b^{\gcd(n,m)}\),其中 \(\gcd(a,b)=1\)
- \(\sum\limits_{i=1}^n gcd (i,n)=∑_{d∣n} d \times \phi(n/d)\)
Ⅲ. 数论分块
数论分块可以快速计算一些形如 \(\sum\limits_{i=1}^{n}f(i)g(\lfloor\frac{n}{i}\rfloor)\) 的和式,时间复杂度为 \(\Theta(\sqrt n)\)。
令\(D(n)= \{ \lfloor \frac{n}{i} \rfloor : 1\le i \le n,i \in \mathbb{N}_{+} \}\),则有以下性质:
\(A.|D(n)|=\lfloor\sqrt{4n+1}\rfloor-1\le 2\sqrt n\).
\(B.\)对于 \(d \in D(n)\),满足\(\lfloor\frac{n}{i}\rfloor=d\) 的 \(i\) 范围是 \(\lfloor\frac{n}{d+1}+1\rfloor\le i \le \lfloor\frac{n}{d}\rfloor\).
\(C.\) 对于 \(m\in D(n)\),有 \(𝐷(𝑚)\subset 𝐷(𝑛)\).
由性质B,我们枚举 \(l\) 从 \(1\to n\),对于每一个块,我们令 \(r \gets \lfloor\frac{n}{\lfloor n/l \rfloor}\rfloor\),此时这个块的贡献是 \(\sum\limits_{i=l}^{r}f(i)*g(\lfloor\frac{n}{l}\rfloor)\)。此时令\(l=r+1\),开始统计下一个块。这样就完成了数论分块。
Ⅳ.积性函数
如果 \(\forall a,b \in \mathbb{N}^\star\) 且 \(a,b\) 互质时,满足 \(f(ab)=f(a) \times f(b)\) 的函数 \(f\) 称为积性函数.
如果 \(\forall a,b \in \mathbb{N}^\star\) 时,都满足 \(f(ab)=f(a) \times f(b)\) 的函数 \(f\) 称为完全积性函数。
积性函数实际上是由欧拉函数推广到一般的函数上得到的概念。

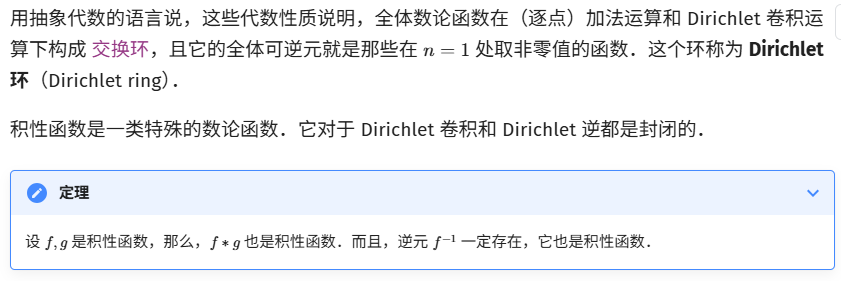
Ⅴ.狄利克雷卷积











 浙公网安备 33010602011771号
浙公网安备 33010602011771号