10.2 CSP-J mock
抽象。J组模拟题做成这个样子。但感觉J~S之间?
\(100+100+10+10=220 pts\)
T1 小 Z 买礼物
题目描述
小 Z 要去给朋友买礼物。
前面有 \(n\) 个人在排队,其中有一些独自前来的顾客和一些组团前来的顾客。
相邻的穿着一样的衣服的顾客在同一团队里。
一个团队里只要第一个人买了就会离开。
问小 Z 会在第几个排到。
输入格式
第一行一个 \(n\), 表示前面有多少个人。
接下来共 \(n\) 行,第 \(i\) 行一个大写英文字母,表示第 \(i\) 个人的衣服颜色。
输出格式
一行,表示小 Z 是第几个排到的。
输入输出样例 #1
输入 #1
6
C
C
P
C
Z
Z
输出 #1
5
说明/提示
【样例解释】
\(CCPCZZ\) 中,排队买到东西的顺序为 \(CPCZ\),所以,小 Z 会在第 5 个排到。
【数据范围】
\(n \le 25\),衣服颜色在 \(A-Z\) 之间。
Sol
模拟即可。
#include<bits/stdc++.h>
using namespace std;
char a[50];
int main(){
int n,sum=2;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
char now=a[1];
for(int i=2;i<=n;i++){
if(a[i]!=now){
now=a[i];
sum++;
}else continue;
}
cout<<sum;
return 0;
}
T2 编程考试
题目描述
小 Z 正在准备编程考试,向你寻求帮助。
给定字符串 \(S\) 及 \(Q\) 次查询。
每次查询给定正整数 \(A,B,C,D\),令字符串 \(X\) 由 \(S\) 中位置(字符串的位置都从 \(1\) 开始计数) \(A\) 到 \(B\) 之间的字符组成,\(Y\) 由 \(S\) 中位置 \(C\) 到 \(D\) 之间的字符组成,你需要判断能否以某种方式重新排列 \(Y\) 中的字符使 \(X\) 与 \(Y\) 相同。
若可以,则输出 DA,否则输出 NE。
输入格式
第一行输入包含字符串 \(S(1 \le |S| \le 50000)\),由英文字母的小写字母组成。
第二行输入包含正整数 \(Q(1 \le Q \le 50000)\)。接下来的 \(Q\) 行,每行给定正整数 \(A,B,C,D\),描述一次询问。
输出格式
对于每个查询,如果可能,输出 DA;如果不可能,则输出 NE。
输入输出样例 #1
输入 #1
kileanimal
2
2 2 7 7
1 4 6 7
输出 #1
DA
NE
输入输出样例 #2
输入 #2
abababba
2
3 5 1 3
1 2 7 8
输出 #2
DA
DA
输入输出样例 #3
输入 #3
vodevovode
2
5 8 3 6
2 5 3 6
输出 #3
NE
DA
说明/提示
【样例 1 解释】
第一次询问,X="i",Y="i",显然 \(Y\) 就是 \(X\),输出 DA。
第二次询问,X="kile",Y="ni",\(Y\) 的长度和 \(X\) 不相同,不管怎么排列都不可能变成 \(X\),所以输出 NE。
【数据范围】
对于 \(50\%\) 的数据满足,\(1 \le |S|,Q \le 10^3\)。
对于 \(100\%\) 的数据满足,\(1 \le |S|,Q \le 50000, 1 \le A,B,C,D \le |S|\),并且保证字符串中的所有字符都是小写字母。
Sol
前缀和即可。
#include<bits/stdc++.h>
using namespace std;
const int M=50005;
int Lim[M][30];
int main(){
string ss;
cin>>ss;
for(int i=0;i<ss.size();i++){
int pw=ss[i]-'a'+1;
for(int j=1;j<=26;j++){
Lim[i+1][j]=Lim[i][j];
}
Lim[i+1][pw]++;
}
int Q;
cin>>Q;
while(Q--){
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
bool flg=true;
for(int i=1;i<=26;i++){
if(Lim[b][i]-Lim[a-1][i]!=Lim[d][i]-Lim[c-1][i]){
printf("NE\n");
flg=false;
break;
}
}
if(flg)printf("DA\n");
}
return 0;
}
T3 最佳程序员
题目描述
小 Z 所在的公司要开始评选最佳程序员了,最后要评选两个人出来。
这个公司一共有 \(n\) 个员工,编号分别为 \(1,2,\dots,n\),每个人把自己心中的两名最佳程序员 \(a\) 和 \(b\) 告诉小 Z。
- 可能存在两个人,他们心中的两名最佳程序员是相同的。例如样例 1 所示。
现在小 Z 要选出两个人,为了让员工满意,至少需要 \(m\) 个人同意最后的决定。所谓同意指的是,某公司员工同意这最终名单,当且仅当该员工心中的两名最佳程序员至少有一个出现在最终名单里。
请你帮小 Z 算算,有多少种可能的组合(与选出来的人的顺序无关),符合条件。
输入格式
第一行两个整数 \(n\) 和 \(m\)。
接下来 \(n\) 行,每行两个整数 \(a\) 和 \(b\),表示一个员工心中的两名最佳程序员的编号。
输出格式
输出有多少种组合满足条件。
输入输出样例 #1
输入 #1
4 2
2 3
1 4
1 4
2 1
输出 #1
6
输入输出样例 #2
输入 #2
8 6
5 6
5 7
5 8
6 2
2 1
7 3
1 3
1 4
输出 #2
1
说明/提示
【样例 1 解释】
\((1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\) 这 \(6\) 种组合,都至少有 \(2\) 名队员同意。
【数据范围】
对于 \(60\%\) 的数据,\(n\) 的范围 \([3,10^4]\);
对于 \(100\%\) 的数据,\(n\) 的范围 \([3,10^5]\), \(m\) 的范围 \([0,n]\),并且保证 \(a≠b,1≤a,b≤n\)。
Sol
我们不能枚举每⼀对组合,所以我们考虑枚举\(i\),如何快速算出满⾜条件的\(j\)的点数。
枚举\(i\),我们可以知道\(j\)的度数⾄少应该为\(m-deg_i\),所有度数⼤于等于 \(d\) 的点都可能成为答案,所以我们可以⽤⼀个后缀和来维护度数⼤于等于 \(d\) 的点的个数。但是,这些答案中有⼀些是⾮法的,例如:
- 如果 i 这个点的度数也⼤于等于 d,不能成为答案
- 如果 i 和 j 直接相连,那么 实际有⽤的度数应该减去直接与 i 相连的边,这个答案也是⾮法的,需要排除
- 因为题⽬可能有重边,所以删除的时候要保证不会重复删除
- 这⼀点,我们可以通过枚举 i 的邻接点实现
#include<bits/stdc++.h>
using namespace std;
const int M=1e5+5;
int deg[M],cnt[M],sum[M],num[M],n,m;
bool vis[M];
vector<int>g[M];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
int a,b;
scanf("%d%d",&a,&b);
++deg[a],++deg[b];
g[a].push_back(b);
g[b].push_back(a);
}
for(int i=1;i<=n;i++)++cnt[deg[i]];
for(int i=n;i;i--)sum[i]=sum[i+1]+cnt[i];
long long ans=0;
for(int i=1;i<=n;i++){
int d=m-deg[i];
if(d<=0)ans+=n-1;
else {
int tmp=sum[d];
if(deg[i]>=d)--tmp;
for(int j=0;j<g[i].size();j++){
int v=g[i][j];
num[v]=0;
vis[v]=false;
}
for(int j=0;j<g[i].size();j++){
int v=g[i][j];
++num[v];
}
for(int j=0;j<g[i].size();j++){
int v=g[i][j];
if(vis[v]) continue;
vis[v]=true;
if(deg[v]>=d&°[v]-num[v]<d)--tmp;
}
ans+=tmp;
}
}
printf("%lld",ans>>1);
return 0;
}
T4 交叉匹配
题目描述
小 Z 有两个正整数数列,如果第一个数列中有一个数和第二个数列中的某个数相同,并且都为 \(r\),则我们可以将这两个数用线段连起来。我们称这条线段为 \(r\)-匹配线段。
小 Z 想要对于给定的输入,找到画出最多匹配线段的方式,并且满足以下条件:
-
每条 \(a\)-匹配线段 恰好和一条 \(b\)-匹配线段 相交,且 \(a \neq b\)(\(a\),\(b\) 表示任何值,并非某个特定的值)。我们称这样的匹配为交叉匹配。
-
不允许两条线段从同一个数出发。例如,下图所示的匹配是错误的。
-
不允许一条线段和多条其它线段相交。
编一个程序对于给定输入数据,计算匹配线段的最多条数。
注意这个数总是偶数。
输入格式
输入第一行,两个整数 \(N1, N2\),分别表示第一个数列和第二个数列的长度。
输入第二行,\(N1\) 个整数,表示第一个数列。
输入第三行,\(N2\) 个整数,表示第二个数列。
输出格式
输出仅一行,表示最多匹配线段的条数。
输入输出样例 #1
输入 #1
6 6
1 3 1 3 1 3
3 1 3 1 3 1
输出 #1
6
输入输出样例 #2
输入 #2
12 11
1 2 3 3 2 4 1 5 3 5 10 4
3 1 2 3 2 4 12 1 5 5 3
输出 #2
6
说明/提示
【样例 1 解释】
如下图所示方案是最佳的,总共有 \(6\) 条线段。
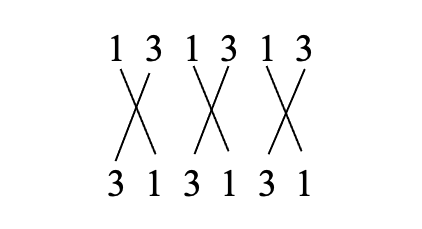
【数据范围】
对于 \(30\%\) 的数据,\(1\le N1, N2 \le 15\);
对于 \(70\%\) 的数据,\(1 \le N1, N2 \le100\);
对于 \(100\%\) 的数据,\(1 \le N1, N2 \le 2000\)。
Sol
显然DP。如果在\(i,j\)处要有两条相交的线段,⼀定会存在\(a_x=b_i\)且\(a_y=b_j\): 并且\(x,y\)是最接近\(i,j\)的,这样显然不劣。
所以预处理出两个\(find[i][j]\),表示\(a[i]\)之前最接近 \(i\) 的与 \(b[j]\) 相同的位置以及 \(b[j]\) 之前最接近 \(j\) 的与 \(a[i]\) 相同的位置。
然后类似最长公共子序列,\(dp[i][j]=\max(dp[x-1][y],dp[x][y-1],dp[i][j])\),递推即可。
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int M=2005;
int a[M],b[M],dp[M][M],f1[M][M],f2[M][M];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=m;i++){
cin>>b[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i-1]==b[j])f1[i][j]=i-1;
else f1[i][j]=f1[i-1][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i]==b[j-1])f2[i][j]=j-1;
else f2[i][j]=f2[i][j-1];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
if(a[i]==b[j]) continue;
if(f1[i][j]&&f2[i][j]){
int k1=f1[i][j],k2=f2[i][j];
dp[i][j]=max(dp[i][j],dp[k1-1][k2-1]+2);
}
}
}
cout<<dp[n][m];
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号