Codeforces Gym 102538 G. Giant Penguin (300iq Contest 3) 题解

题目链接

不错的点分树题。我之前只听说过有点分树这个东西，没做过几个题。

先考虑图是一棵树的情况怎么做。我们对这棵树建立点分树。所谓点分树，就是先对树进行重心分治(点分治)，然后把相邻两层的重心连边形成一棵新的树。容易发现新的树的高度是\(O(logn)\)的。看一开始重心分治的过程，在重心分治的每一层里，我们处理原树中所有满足"两个端点都在这一层内，且端点分别在重心的不同子树"的路径，路径指的是从标记点到询问点的路径。比如当前层的重心是c，我们要处理其两个不同子树内点x和点y之间的路径。在点分树中，c肯定是x和y的LCA。假设我们在某一次修改时标记了x，之后又询问了y，为了让x能更新到y的答案，我们给每个点设置一个权值\(val_i\)，在标记x时给它的所有(点分树上的)祖先的\(val_i\)都更新上从那个祖先到x的距离；询问y时枚举y的所有祖先，用每个祖先的\(val_i\)加上从它到y的距离更新答案即可。这样每对(x,y)都在其LCA处(也就是它们被分开的那一层的重心)被统计了。时间复杂度\(O(nlogn)\)。

原问题可以用类似的方法做。我们取原图的一棵生成树建点分树。先来分析重心分治的过程。在分治的每一层里，我们要统计的是在完全这一层内部(不经过这一层外面的点)且跨越子树的路径，有以下两种：


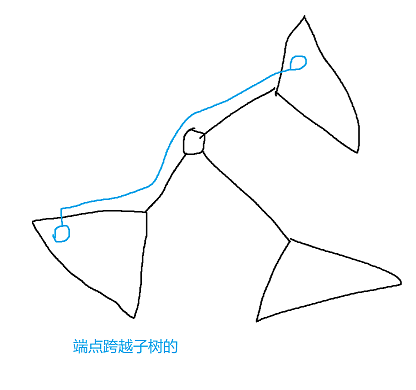
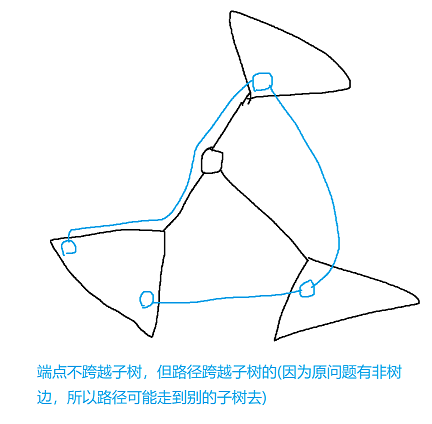
由于每个节点都在最多10个不经过重复点的环内，所以在层内所有的边中，最多只有k条是跨越子树的，因为每条这种边都能构成至少一个包含重心的简单环。层内边指的是两个端点都在层内的边。发现这一层内需要统计的所有路径，要么经过重心，要么经过至少一条跨越子树的边。把重心设为"关键点"，每条跨越子树的边也随便选一个点作为关键点，则每条要统计的边至少经过一个关键点，且每层关键点个数不超过k+1个。不妨像树的情况在重心处统计路径那样，我们在这些关键点处统计路径。我们以每个关键点为原点，用层内的点和边跑bfs，求出每个关键点到层内每个点的最短路。类似地，在标记一个点x时，枚举它(点分树上)所有的祖先，并更新这个祖先所在层的所有关键点的值。询问时类似。注意不要用map存距离，多一个log卡不过去的。(亲身试验) 可以用\(dist[pos][lev][i]\)表示点pos到它的第lev级祖先所在层的第i个关键点的距离。

时间复杂度\(O(nklogn)\)。

点击查看代码

#include <bits/stdc++.h>

#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back

void fileio()
{
  #ifdef LGS
  freopen("in.txt","r",stdin);
  freopen("out.txt","w",stdout);
  #endif
}
void termin()
{
  #ifdef LGS
  std::cout<<"\n\nPROGRAM TERMINATED";
  #endif
  exit(0);
}

using namespace std;

int n,m,t,fa[100010],sz[100010],col[100010],len,dis[100010],finalpar[100010],dep[100010],dist[100010][20][12],inList[100010],mark=0;
vector <int> g[100010],tg[100010],ttg[100010],List;
vector <pii> e,implist[100010];
vector <pair <pii,pii> > dists;//{{id,up},{dn,dist}}
bool ban[100010];
pii mn;

int Find(int x){return fa[x]==x ? x:fa[x]=Find(fa[x]);}

void dfsSz(int pos,int par)
{
  sz[pos]=1;
  rep(i,tg[pos].size()) if(tg[pos][i]!=par&& !ban[tg[pos][i]]) dfsSz(tg[pos][i],pos),sz[pos]+=sz[tg[pos][i]];
}
void getCen(int pos,int par,int tot)
{
  int val=tot-sz[pos];
  rep(i,tg[pos].size()) if(tg[pos][i]!=par&& !ban[tg[pos][i]]) val=max(val,sz[tg[pos][i]]),getCen(tg[pos][i],pos,tot);
  mn=min(mn,mpr(val,pos));
}
void dfsColor(int pos,int par)
{
  col[pos]=len;List.pb(pos);
  rep(i,tg[pos].size()) if(tg[pos][i]!=par&& !ban[tg[pos][i]]) dfsColor(tg[pos][i],pos);
}
int solve(int pos,int d)//建立点分树
{
  dfsSz(pos,0);
  mn=mpr(1e9,1e9);getCen(pos,0,sz[pos]);
  pos=mn.se;dep[pos]=d;
  len=0;List={pos};
  rep(i,tg[pos].size()) if(!ban[tg[pos][i]])
  {
    ++len;
    dfsColor(tg[pos][i],pos);
  }
  vector <int> imp={pos};
  ++mark;rep(i,List.size()) inList[List[i]]=mark;
  rep(i,List.size()) rep(j,g[List[i]].size())
    if(!ban[g[List[i]][j]]&&col[List[i]]!=col[g[List[i]][j]]&&List[i]!=pos&&g[List[i]][j]!=pos&&inList[g[List[i]][j]]==mark)
      imp.pb(min(List[i],g[List[i]][j]));
  sort(imp.begin(),imp.end());imp.erase(unique(imp.begin(),imp.end()),imp.end());
  rep(i,imp.size()) implist[pos].pb(mpr(imp[i],1e9));
  rep(i,imp.size())
  {
    rep(j,List.size()) dis[List[j]]=1e9;
    queue <LL> qq;qq.push(imp[i]);dis[imp[i]]=0;
    while(!qq.empty())
    {
      int f=qq.front();qq.pop();
      rep(j,g[f].size()) if(!ban[g[f][j]]&&dis[g[f][j]]>dis[f]+1)
      {
        dis[g[f][j]]=dis[f]+1;
        qq.push(g[f][j]);
      }
    }
    rep(j,List.size()) dists.pb(mpr(mpr(i,pos),mpr(List[j],dis[List[j]])));
  }
  ban[pos]=true;
  rep(i,tg[pos].size()) if(!ban[tg[pos][i]])
  {
    int nxt=solve(tg[pos][i],d+1);
    ttg[pos].pb(nxt);finalpar[nxt]=pos;
  }
  return pos;
}

void chmin(int &x,int y){if(x>y) x=y;}

int main()
{
  fileio();

  cin>>n>>m>>t;
  int x,y;
  rep(i,m)
  {
    scanf("%d%d",&x,&y);
    g[x].pb(y);g[y].pb(x);
    e.pb(mpr(x,y));
  }
  repn(i,n) fa[i]=i;
  rep(i,e.size()) if(Find(e[i].fi)!=Find(e[i].se))
  {
    tg[e[i].fi].pb(e[i].se);tg[e[i].se].pb(e[i].fi);
    fa[Find(e[i].fi)]=Find(e[i].se);
  }
  int root=solve(1,0);
  rep(i,dists.size()) dist[dists[i].se.fi][dep[dists[i].se.fi]-dep[dists[i].fi.se]][dists[i].fi.fi]=dists[i].se.se;

  int q;cin>>q;
  rep(qn,q)
  {
    scanf("%d%d",&x,&y);
    if(x==1)
    {
      int cur=y,cc=0;
      while(true)
      {
        rep(i,implist[cur].size()) chmin(implist[cur][i].se,dist[y][cc][i]);
        if(cur==root) break;
        cur=finalpar[cur];++cc;
      }
    }
    else
    {
      int ans=1e9,cur=y,cc=0;
      while(true)
      {
        rep(i,implist[cur].size()) chmin(ans,implist[cur][i].se+dist[y][cc][i]);
        if(cur==root) break;
        cur=finalpar[cur];++cc;
      }
      printf("%d\n",ans);
    }
  }

  termin();
}

PS: 官方题解英语水平太差了，完全看不懂