巧克力糖果（chocolate）

题目描述

你的工厂里有 \(n\) 个车间，每个车间里都有大量糖果。它们通过 \(n-1\) 条管道连接在一起，每个管道有特定的巧克力酱输送时间 \(w_i\)。

两个关键车间 \(a\) 和 \(b\) 已在一开始储满顶级巧克力酱，它们能通过相邻管道向其他车间输送巧克力。

每次，有巧克力的车间可选择一个相邻糖果车间（也只能选择一个）开始输送，这将花费对应的运输时间，运输中途不可以中断，不可以更改输送目标。时间结束后，另一个糖果车间将充满巧克力酱。（不同车间的输送可同时进行）新的充满巧克力浆的车间可立即开始输送任务。

你当然知道巧克力酱时间长的会冷却凝固，影响糖果光泽。所以，你希望知道，通过合理安排巧克力酱传递顺序，让每个车间都被输送巧克力酱需要的最少时间是多少？

数据范围

对于所有测试数据，保证：\(2\le n\le2\times10^5 , 1\le a,b\le n,a\not=b,1\le x_i,y_i\le n,x_i\not=y_i,1\le w_i \le 10^9\)

题解

先只考虑只有一个初始车间的情况，并且 \(w_i=1\) 的特殊情况。

设 \(f_i\) 表示把以 \(i\) 为根的子树全部运入巧克力酱的时间。

对于叶子结点， \(f_i=0\) ；

对于非叶子结点，当仅有 \(1\) 颗子树时，显然 \(f_i=f_{k \in subtree(x)}+1\) 。当子树颗数不止 \(1\) 颗我们需要考虑运输顺序。可以证明，我们应该按照 \(f_{k \in subtree(x)}\) 从大到小的顺序染色为最优。

证明：（邻项交换）

设 \(f_{k_1 \in subtree(i)}\) 和 \(f_{k_2 \in subtree(i)}\) 满足 \(f_{k1}>f_{k2}\) 且有且仅有 \(k_1\), \(k_2\) 两颗子树。

若先对 \(k_1\) 运输，则 $ f_i=\max (f_{k_1}+1,f_{k_2}+2)$ （\(+1\) 是 \(k_1\) 的运输时间，\(+2\) 是 \(k_2\) 等待 \(k_1\) 根节点先运输的时间加上自己的运输时间）。

假设交换顺序：先对 \(k_2\) 运输，则 \(f_i=\max (f_{k_1}+1,f_{k_2})+1\) （含义同上，只是把 \(+1\) 给提出来了）。

由 \(f_{k1}>f_{k2}\) 可得：

\[\begin{cases} f_{k1}+1>f_{k2}+1 \\ f_{k1}+1>f_{k1} \end{cases} \]

因此可得 \(\max (f_{k_1},f_{k_2}+1)<f_{k_1}+1\)，即 \(\max (f_{k_1},f_{k_2}+1)+1<\max (f_{k_1}+1,f_{k_2})+1\)。所以可知，在交换前更优，该结论可以推广到子树颗数大于等于 \(2\) 的情况下。

如果 \(w_i\) 不一定为 \(1\) 呢？我们继续通过邻项交换来证明。

证明：

设出 \(f_{k_1 \in subtree(i)}\) 和 \(f_{k_2 \in subtree(i)}\) ，\(i\) 节点有且仅有 \(k_1\), \(k_2\) 两颗子树。（\(w_{k_1}\) 和 \(w_{k_2}\) 分别表示 \(i\) 节点到 \(k_1\) 和 \(k_2\) 的边权值）（此处没有规定谁大，与上一个证明不同）

若先对 \(k_1\) 运输，\(f_1=\max(f_{k_1}+w_{k_1},f_{k_2}+w_{k_1}+w_{k_2})\)。

若先对 \(k_2\) 运输，\(f_2=\max(f_{k_1}+w_{k_1}+w_{k_2},f_{k_2}+w_{k_2})\)。

分类讨论：（下面三种情况一定覆盖了所有情况且不会出现同时满足的情况）

1. \(f_{k_1}\ge f_{k_2}+w_{k_2}\)

   此时 \(f_1=f_{k_1}+w_{k_1}\)，显然 \(f_2=f_{k_1}+w_{k_1}+w_{k_2}\)​。

   显然 \(f_1<f_2\)，我们应该先对 \(k_1\) 运输。

2. \(f_{k_1}+w_{k_1}\le f_{k_2}\)

   此时 \(f_2=f_{k_2}+w_{k_2}\)，显然 \(f_1=f_{k_2}+w_{k_1}+w_{k_2}\)​。

   显然 \(f_1>f_2\)，我们应该先对 \(k_2\) 运输。

3. \(f_{k_1}<f_{k_2}+w_{k_2}\) 且 \(f_{k_1}+w_{k_1}>f_{k_2}\)

   此时 \(f_1=f_{k_2}+w_{k_1}+w_{k_2},f_2=f_{k_1}+w_{k_1}+w_{k_2}\)。

   容易发现，若 \(f_{k_1}\) 更小，我们应先对 \(k_2\) 运输，若 \(f_{k_2}\) 更小，我们应先对 \(k_1\) 运输。相等则均可。

再重新审视前两种情况，发现也符合情况 \(3\) 的结论。该结论可以推广到子树颗数大于等于 \(2\) 的情况下。

所以，我们还是对 \(f_k\) 从大到小排序选择即可。

那如果现在有两个初始车间呢？我们找出两个点之间的这条路径，枚举切断哪一条边，这样分成两棵树，一半给一个初始车间完成。最后的答案是两棵树的答案的最大值。现在可以发现单调性：切断的边距离初始车间越远，该车间所在的树完成的时间一定不会减少。

画图：（横轴为这条路径，左侧初始车间答案对应绿色线，右侧初始车间答案对应红色线。实线为最终的答案）

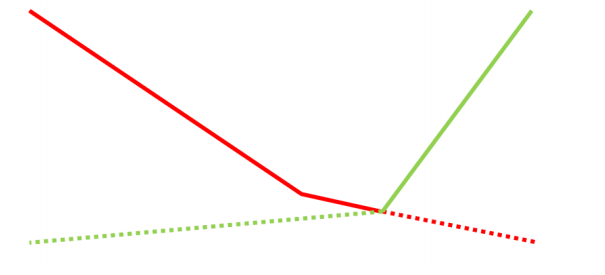
可以发现，答案是一个非严格的凹函数，但是，由于不是严格单调的，我们不能三分。（可能可以用爬山算法乱搞试试）

再次观察：左侧的一段前驱，其答案来自一棵树；右侧的一段后驱，其答案来自另一棵树。这是二分的两段性。我们二分最右侧的以左子树为答案的点。然后我们的答案一定来自这个点和这个点往右一个点（最左侧的以右子树为答案的点）。（如果相等给谁都可以，但要统一）

时间复杂度 \(O(n\log^2 n)\)。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=4e5+5;
int ver[M],edge[M],nxt[M],head[N],tot=1;
int v[N],cnt=0;
int n,a,b,disable;
bool fd;
long long f[N];
const int SIZE=1<<23;
char buf[SIZE],*p_1=buf,*p_2=buf,pbuf[SIZE],*p_=pbuf;
#define getchar() (p_1==p_2&&(p_2=(p_1=buf)+fread(buf,1,SIZE,stdin),p_1==p_2)?EOF:*p_1++)
#define putchar(c) (p_-pbuf==SIZE?(fwrite(pbuf,1,SIZE,stdout),p_=pbuf,*p_++=(c)):*p_++=(c))
#ifdef putchar
#define flush fwrite(pbuf,1,p_-pbuf,stdout),p_=pbuf,0
#else
#define flush 0
#endif
inline int read()
{
	int x=0,f=1; char c=getchar();
	while (c<'0'||c>'9') f=(c=='-'?-1:f),c=getchar();
	while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}
char out_[40];
inline void write(long long x)
{
	if (x<0) x=-x,putchar('-');
	int cnt=0;
	do out_[++cnt]=(char)((x%10)^48),x/=10; while (x);
	while (cnt) putchar(out_[cnt--]);
}
inline void addedge(const int &x,const int &y,const int &w)
{
	ver[++tot]=y,edge[tot]=w,nxt[tot]=head[x],head[x]=tot;
}
inline void dfs(const int &x,const int &fa)
{
	if (x==b) { fd=true; return; }
	for (int i=head[x];i;i=nxt[i]) if (ver[i]!=fa)
	{
		v[++cnt]=i,dfs(ver[i],x);
		if (fd) return; 
		--cnt;
	}
}
inline void dp(const int &x,const int &fa)
{
	int cnt=0;
	for (int i=head[x];i;i=nxt[i]) if (ver[i]!=fa&&disable!=i&&(disable^1)!=i)
		dp(ver[i],x),++cnt;
	vector < pair<long long,int> > son(cnt);
	for (int i=head[x];i;i=nxt[i]) if (ver[i]!=fa&&disable!=i&&(disable^1)!=i)
		son[--cnt]=make_pair(f[ver[i]],edge[i]);
	sort(son.begin(),son.end(),[](const auto &x,const auto &y){ return x.first>y.first; });
	long long res=0,ans=0;
	for (auto s:son) res+=s.second,ans=max(ans,res+s.first);
	f[x]=ans;
}
inline bool check(const int &x)
{
	disable=v[x];
	dp(a,0),dp(b,0);
	return f[a]<f[b];
}
int main()
{
//	freopen("chocolate.in","r",stdin);
//	freopen("chocolate.out","w",stdout); 
	n=read(),a=read(),b=read();
	for (int i=1;i<n;i++)
	{
		int x=read(),y=read(),w=read();
		addedge(x,y,w),addedge(y,x,w);
	}
	dfs(a,0);
	int l=0,r=cnt;
	while (l<r)
	{
		int mid=(l+r+1)>>1;
		if (check(mid)) l=mid;
		else r=mid-1;
	}
	long long ans=0x7fffffffffffffff;
	if (l) check(l),ans=min(ans,max(f[a],f[b]));
	if (l+1<=cnt) check(l+1),ans=min(ans,max(f[a],f[b]));
	write(ans);
	return flush;
}