动态规划思考题 1

CF1542D

容易想到对每个数字计算方案数，接下来可接受的复杂度是 \(O(n^2)\)，考虑设计一个二维 \(f_{i.j}\) 表示前 \(i\) 个数选出来有 \(j\) 个比这个数小的方案数，特别的，数字大小相同时按位置大小比较，原理是我们不在于具体的数字大小，只在意这个数比选的数大还是小。

考虑转移，发现是 \(O(1)\) 的，注意特判 \(f_{i,0}\) 的转移不太一样即可。

CF1131G

容易根据数据范围得到状态 \(f_i\) 表示只考虑前 \(i\) 个牌并推倒前 \(i\) 个牌的最小代价。原因是这样转移没有啥后效性。

从每个点开始 \(dp\)，可以得到如下式子：

• 向左推倒第 \(i\) 个骨牌，由于最多只能推倒 \(l_i\)，\([l_i,i)\) 这些是可以选择性在 \(i\) 之前推的，所以这部分答案为
  \[\min\{f_j|l_i-1\le j< i\}+c_i \]

• 不推倒第 \(i\) 个骨牌，那么必须由前面的某个骨牌向右推倒，答案为
  \[\min\{f_{j-1}+c_j|j<i\le r_j\} \]

发现第一个转移可以优化为 \(f_{l_i-1}+c_i\)，具体原因可以证明：

• 若最优解是从 \(i\) 向左推，但是从 \(l_i-1\le j<i\) 的点也需要推动，那么只有 \(i\) 的后缀的那一部分向右倒才可能更优，与假设矛盾，所以可以优化这个转移。

用单调栈维护 \(l_i,r_i\) 是简单的，具体来说就是 \(i\) 能推倒 \(i+1\) 就把 \(i+1\) 加入，否则就退栈并赋值直到能加入或者栈空。

接下来考虑怎么优化，这个推牌的 \([i,r_i]\) 是很有意思的，根据 \(l_i,r_i\) 的求法我们发现任意两个区间只可能是包含或者相离的关系。所以我们把这个包含关系转化成树上的父亲儿子关系。那么这些个区间就会形成树，我们要求的值也就是到根的链的最小值。看看怎么做。

我们可以在从左向右走到这个点的时候将其加入树，集体来说就是加入这个点本来对应的区间的儿子，然后两个区间对应的值取 \(\min\)，如果离开了这个区间，那么就一直跳父亲直到可以容下下一个点。然后继续取 \(\min\)。

CF1781F

以前讲题被这个题折磨惨了，不做。

推荐阅读题解

CF1140G

树上倍增妙题

题意

两颗同构的树，对应的节点间连边，边有正边权，回答 \(q\) 次询问，每次询问两节点 \(u,v\) 之间的最短路。

思路

约定记号：若 \(u\) 是树 \(1\) 上某点，则 \(u'\) 为其在树 2 上的对应点。

假如现在只有一棵树，那么倍增处理树上路径即可。

现在有两棵树，切换树可能有三种情况：跳到父亲换，跳到子树换，直接换。设 \(w[u]\) 为在 \(u\) 点换树的代价。

首先有 \(w[u]\) 在 \(u\) 点直接换树的代价。现在考虑跳到父亲或儿子换树的可能性。

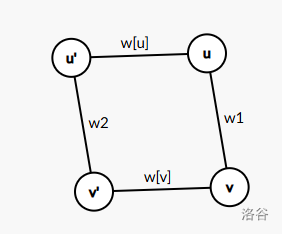
设 \(v\) 为 \(u\) 儿子，\(w_1,w_2\) 为 \((u,v)\) 在两棵树中的边权，有：

\[w[u]=\min(w[u],w[v]+w_1+w_2) \]

和

\[w[v]=\min(w[v],w[u]+w_1+w_2) \]

据此进行两次 dfs 求出 \(w[u]\)。

然后是倍增求 lca，与树上路径相似，设 \(dp[i][j][0/1][0/1]\) 为 \(i\) 点往上跳 \(2^j\) 步，起点是/否在 \(1\) 号树，终点是否在 \(1\) 号树的最小权值。

考虑先求初始状态，还是上面的那个图。

从 \(v\) 到 \(u\) 有两种情况，直接走 \((u,v)\) 间的连边 \(w_1\)，或者换树走，\(v\rightarrow v'\rightarrow u'\rightarrow u\)，权值 \(w[v]+w[u]+w_2\)。其它情况同理。

所以有转移：

\[\operatorname{dp}[v][0][0][0]=\min(w1,w[v]+w_2+w[u]) \]

\[\operatorname{dp}[v][0][0][1]=\min(w_1+w[u],w[v]+w_2) \]

\[\operatorname{dp}[v][0][1][0]=\min(w_1+w[v],w[u]+w_2) \]

\[\operatorname{dp}[v][0][1][1]=\min(w_2,w[v]+w_1+w[u]) \]

初始状态完考虑倍增。倍增要复杂一些，建议配合图来理解。

求出 \(\operatorname{dp}[i][j][0/1][0/1]\) 需要分两步跳，首先跳到 \(\operatorname{fa}[i][j-1]\) ，然后跳到 \(\operatorname{fa}[\operatorname{fa}[i][j-1]][j-1]\) 即 \(\operatorname{fa}[i][j]\)。

下面设 \(a\) 点为 \(\operatorname{fa}[i][j-1]\)，\(b\) 点为 \(\operatorname{fa}[i][j]\)，以 \(i\) 点转移到 \(b\) 点为例：

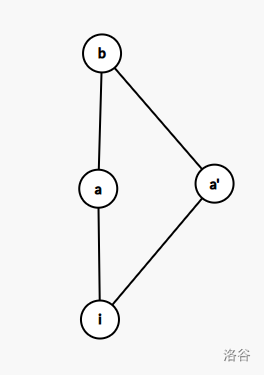
显然有 \(i\rightarrow a\rightarrow b\) 和 \(i\rightarrow a'\rightarrow b\) 两种走法，得到转移：

\[\operatorname{dp}[u][i][0][0]=\min(\operatorname{dp}[u][i-1][0][0]+\operatorname{dp}[fa[u][i-1]][i-1][0][0],\operatorname{dp}[u][i-1][0][1]+\operatorname{dp}[fa[u][i-1]][i-1][1][0]) \]

其余同理，得到：

\[\operatorname{dp}[u][i][0][1]=\min(\operatorname{dp}[u][i-1][0][0]+\operatorname{dp}[fa[u][i-1]][i-1][0][1],\operatorname{dp}[u][i-1][0][1]+\operatorname{dp}[fa[u][i-1]][i-1][1][1]) \]

\[\operatorname{dp}[u][i][1][0]=\min(\operatorname{dp}[u][i-1][1][0]+dp[fa[u][i-1]][i-1][0][0],\operatorname{dp}[u][i-1][1][1]+\operatorname{dp}[fa[u][i-1]][i-1][1][0]) \]

\[\operatorname{dp}[u][i][1][1]=\min(\operatorname{dp}[u][i-1][1][0]+\operatorname{dp}[fa[u][i-1]][i-1][0][1],\operatorname{dp}[u][i-1][1][1]+\operatorname{dp}[fa[u][i-1]][i-1][1][1]) \]

至此预处理完成。考虑询问。

先把询问的点编号转换成我们树上的编号，即 $u\leftarrow \left \lfloor \frac{u+1}{2} \right \rfloor , v\leftarrow \left \lfloor \frac{v+1}{2} \right \rfloor $，并判断两点所在树的编号。

肯定先求 lca，求完后设 \(\operatorname{dpu}[0/1]\) 表示 \(u\) 跳到 lca 时在树 1/2 的代价，\(\operatorname{dpv}[0/1]\) 同理。

所以倍增跳即可。

答案即为 \(\min(dpu[0]+dpv[0],dpu[1]+dpv[1])\)。

思路总结：

1. 考虑普通树上用倍增解决。
2. 扩展到两棵树上用增加维度的方法解决。

CF1279F

题意简化

• 给你一个字符串，长度为 \(n\)，区分大小写，也可看成零一串。
• 每次操作把 \([i,i+len-1]\) 的所有字符变成大写或小写（\(0\) 或 \(1\)），最多可以进行 \(k\) 次操作。
• 你需要最小化大小写字母个数的最小值（或 \(0\)，\(1\) 个数的最小值）。
• \(n,len\le 10^6\)

分析

这里讲正解，我们考虑二分+动规。

摆在我们面前的有两个问题：

• 二分枚举什么？如何判断可行？正确性？
• \(dp_i\) 表示什么？ \(dp_i\) 如何转移？

我们发现每一次操作的长度为 \(len\)，那么每次最多将小写或大写字母的个数减少 \(len\) 个，最少一个都没变。（为了和二分的 \(l\) 区分，这里用了 \(len\)，而不是 \(l\)，注意。）

那么对于小写的情况，我们就可以二分枚举每次操作将小写字母数量最少减少了 \(mid\)。\(dp_i\) 表示经历了若干次操作，当前点为 \(i\) 时，在每次操作最少减少 \(mid\) 个小写字母之外，额外减少的个数（就是还多删了几个）。我们可以判断在当前情况下，所需要的操作次数是否小于等于 \(k\)。这样我们就能找到最小的 \(mid\)。大写字母的情况相同。

二分具体说是这样：

    l = 0, r = len;
    while(l < r){
		int mid = l + r >> 1;
		if(check(mid, 0) <= k)//判断是否满足操作次数小于等于k。
			r = mid;
		else
			l = mid + 1;
    }
    check(l, 1);//表示找到了一个最优解,记录答案。

关于二分的正确性，如果我们找到一个满足的值 \(mid\),它需要的操作次数不大于 \(k\),那么就继续寻找最小的 \(mid\) 值。

关于 \(dp_i\) 的转移：

\[dp_i = \begin{cases} \max(dp_{i-1},sum_i-mid) &\text i<len\\ \max(dp_{i-1},dp_{i-len}+sum_i-sum_{i-len}-mid) &\text i\geq len \end{cases}\]

其中 \(sum_i\) 为 \(a_i\) 的前缀和，对大小写分别计算，\(mid\) 为每次操作最少减少的小写字母数量。

• 第一个式子中， 因为 \(i<len\),那么它不可能是从第一个数之前开始操作的，既它操作的左起点一定小于 \(1\)。它只可能不操作或以 \(1\) 为左起点来操作所以它不是终点。\(sum_i-mid\) 即为在 \([1,i]\) 中多删的个数。

• 第二个式子中，它仍能不操作或在一个操作之间，或者作为一个操作的终点。于是这个操作是从 \(i-len+1\) 开始的。那么 \(sum_i-sum_{i-len}\) 即为在 \([i-len+1,i]\) 中 \(1\) 的个数，减去 \(mid\)，即为这次操作中多去掉的数。它从 \(i-len+1\) 上来，就加上 \(dp_{i-len}\)，于是就有了上述的转移（注意是 \(dp_{i-len}\) 哦）。

我们还需要一个数组 \(ans_i\) 来记录当前在第 \(i\) 位时，每次操作最小减少 \(mid\) 个数，最少需要几次操作。

\[ans_i = \begin{cases} ans_{i-1} &\text x<dp_{i-1}\\ ans_{i-len}+1 &\text x>dp_{i-1} \\ \min(ans_{i-1},ans_{i-len}+1) &\text x=dp_{i-1} \end{cases}\]

\[x = \begin{cases} sum_i-mid &\text i<len\\ dp_{i-len}+sum_i-sum_{i-len}-mid &\text i\geq len \end{cases}\]

\(x\) 其实就是上面求 \(dp_i\) 中，\(\max\) 的右边部分。

不难明白：

• 如果当前多删除的个数比前一个要多，那么肯定以 \(i-len+1\) 处进行一次操作更好。
• 如果比之前小，则不用进行操作，因为还不如之前的。
• 如果等于，则取前一个和第 \(i-len+1\) 个的最小值（但是算的时候是在 \(i-len\) 的）。

那么我们的答案即为：

\[\min(sum_n-dp_n-k\times mid,sum_n-dp_n-k\times mid) \]

上式左右分别是小写和大写的情况。

因为在条件允许的情况下，操作次数肯定越多越好，所以是 \(k\times mid\)。

到这分析完毕。二分复杂度为 \(O(\log n)\), 维护 \(dp_i\) 和 \(ans_i\) 的复杂度为 \(O(n)\)。总复杂度为 \(O(n\log n)\)。

总结

思路为二分+动规，关键点在于二分的条件和状态转移。其实就是带权二分入门。

可以这么理解，就是二分来修改 \(dp\) 的操作限制，这个限制二分了保证可以找到最优点。

下面这个 \(dp\) 的修改和判断部分还是很巧妙的， \(ans\) 的判断部分值得学习。

CF1372E

容易感觉出来是枚举那一列尽量填，但是区间dp不好想到。

同类型题目：P4766。特点：区间dp枚举第一步/最后一步。转态都为所有子区间完全包含在 \([l,r]\) 之间。

难点在于怎么注意到这个类似贪心的放置。

由于是取平方和，所以有明显的结论：一定存在一种最优方案，第 \(1\) 列是全 \(1\) 的。

这个结论看似没什么用，但却可以反应出如下性质：

定义“可取的位置”为：此时其所在区间还没有 \(1\) 的位置。那么答案必定是按照
某个优先级从大到小，逐列把列上所有“可取的位置”都变为 \(1\)。

拿样例解释一下，它优先取第一列，发现当前所有包含了形如 \((i,1)\) 的区间都是全 \(0\) 的，所以贡献为 \(4^2\)；其次是最后一列，发现贡献也是 \(4^2\)；接着是第二列，发现第 \(3\) 行的第二个区间、第 \(4\) 行的第二个区间是全 \(0\) 的，贡献是 \(2^2\)；最后是剩下的 \(3,4\) 两列，贡献都是 \(0^2\)。所以答案是 \(4^2+4^2+2^2+0^2+0^2\)。

会发现上述性质反证法可得。

考虑使用区间 \(\text{DP}\)。\(f_{l,r}\)：满足 \(l \leq l' \leq r' \leq r\) 的所有区间 \([l',r']\) 能得到的最大贡献；再钦定 \(c_{l,r,i}\) 为：满足 \(l \leq l' \leq i \leq r' \leq r\) 的区间对 \([l', r']\) 的个数。

转移显然，枚举 \([l,r]\) 中优先级最高的点 \(i\)：

\[f_{l,r} \gets f_{l,i-1}+f_{i+1,r}+c_{l,r,i} \]

但是现在还存在一个问题：没有完全被 \([l,r]\) 覆盖的区间是否可能对 \(i\) 产生贡献？

其实不然。当我们转移到一个区间时，端点处要不是边界，就是优先级比它高的点。所以不存在这种情况。

\(c\) 的预处理可以看下，是有意思的。

#include <bits/stdc++.h>
#define FL(i, a, b) for(int i = (a); i <= (b); i++)
#define FR(i, a, b) for(int i = (a); i >= (b); i--)
using namespace std;
const int N = 110;
int n, m, f[N][N], c[N][N][N];
int main(){
	scanf("%d%d", &n, &m);
	FL(i, 1, n){
		int len, l, r; scanf("%d", &len);
		FL(j, 1, len){
			scanf("%d%d", &l, &r);
			FL(k, l, r) c[l][r][k]++;
		}
	}
	FL(len, 1, m) FL(l, 1, m - len + 1){
		int r = l + len - 1;
		FL(i, l, r){
			c[l][r][i] += c[l + 1][r][i] + c[l][r - 1][i] - c[l + 1][r - 1][i];
			f[l][r] = max(f[l][r], f[l][i - 1] + f[i + 1][r] + c[l][r][i] * c[l][r][i]);
		}
	}
	printf("%d\n", f[1][m]);
	return 0;
}

CF1279E

我们先套路性 \(x\to p_x\) 连边，可以发现好排列一定有如下性质：

• 每一个环一定是连续的。
• 每一个环第一个点是最大值。

考虑先怎么计数。我们考虑连续段计数，设计 \(f_i\) 表示长度为 \(i\) 的好排列的方案数，\(g_i\) 为长度为 \(i\) 且满足限制的环。

我们容易得到方程：3424

\[f_0=1,f_i=\sum^{i-1}_{J=0}f_j\times g_{i-j} \]

\(g\) 数组也是好求的，考虑连边过程，我们把这个环的遍历过程的下标排成序列，那么第一个数和第二个数的都是确定的，所以答案是 \((n-2)!\)，特殊的 \(g_1=1\)。

现在问题就在于，我们如何构造出字典序第 \(k\) 小的满足条件的排列。

首先假设我们要构造长度为 \(n\) 的第 \(k\) 小的排列 \(p\)，一个显然的思路是先枚举 \(p_1\) 的值。由于 \(p_1\) 的值决定了这个排列第一段的长度，于是 \(p_1\) 的值就很容易确定了。假设求出了 \(p_1=m\)，我们先将 \(k\) 减去 \(p_1\) 取 \(1,\dots,m-1\) 的方案数，此时排列被分成两部分：左边一个长度为 \(m\) 的环，然后是右边一个长度为 \(n-m\) 的排列。由于左边的环具体长什么样对右边的方案数没有影响，那么我们就可以确定左边的环的排名 \(t_1=\lceil\frac{k}{f_{n-m}}\rceil\)，这样也可以确定右边的排列在所有相同长度的排列中排名为 \(t_2=k-(t-1)\times f_{n-m}\)。

对于右边的部分，直接递归就好了，那么问题就是如何算左边的部分。

这个也相当简单，确定 \(p_1\) 之后，我们还是从 \(p_2\) 开始往后一个一个确定对应位置的取值，只是枚举的时候不要让排列在第 \(m\) 个位置之前成环就可以了。时间复杂度 \(O(Tn^3)\)

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const long long INF=1e18+7;
long long f[53],fac[53];
long long add(long long a,long long b)
{
	return min(INF,a+b);
}
long long mul(long long a,long long b)
{
	if(INF/a<b)return INF;
	return a*b;
}
const int N=50;
long long g(int n)
{
	if(n==1)return 1;
	return fac[n-2];
}
void init()
{
	fac[0]=1;
	for(int i=1;i<=N;i++)
		fac[i]=mul(fac[i-1],i);
	f[0]=1;
	for(int i=1;i<=N;i++)
		for(int j=1;j<=i;j++)
			f[i]=add(f[i],mul(f[i-j],g(j)));
	return ;
}
int p[53];
int q[53];
bool vis[53];
int find(int x)
{
	while(q[x])x=q[x];
	return x;
}
void getq(int n,long long k)
{
	if(n==1){
		q[1]=1;
		return ;
	}
	for(int i=1;i<=n;i++)
		q[i]=vis[i]=0;
	q[1]=n;vis[n]=1;
	for(int i=2;i<n;i++)
	{
		long long num=fac[n-i-1];
		for(int j=1;j<=n;j++)
			if(j!=i&&!vis[j]&&find(j)!=i)
			{
				if(k<=num){
					q[i]=j;
					vis[j]=true;
					break;
				}
				k-=num;
			}
	}
	for(int i=1;i<=n;i++)
		if(!vis[i])q[n]=i;
	return ;
}
void getp(int n,long long k)
{
	if(!n)return ;
	int len=0;
	for(int i=1;i<=n;i++)
	{
		long long num=mul(g(i),f[n-i]);
		if(k<=num){
			len=i;
			break;
		}
		k-=num;
	}
	long long num=f[n-len];
	long long need=(k-1)/num+1;
	getp(n-len,k-(need-1)*num);
	for(int i=n;i>len;i--)
		p[i]=p[i-len]+len;
	getq(len,need);
	for(int i=1;i<=len;i++)
		p[i]=q[i];
	return ;
}
int main()
{
	init();
	int t;scanf("%d",&t);
	while(t--)
	{
		int n;long long k;
		scanf("%d %lld",&n,&k);
		if(f[n]<k)printf("-1\n");
		else{
			getp(n,k);
			for(int i=1;i<=n;i++)
				printf("%d ",p[i]);
			printf("\n");
		}
	}
	return 0;
}

CF1295F

题意即 \(a_i\) 在 \([l_i, r_i]\) 等概率随机，求 \(a_{1 \dots n}\) 不增的概率。

跟 P3643 [APIO2016]划艇 几乎一样：\(a_i\) 在 \([l_i, r_i]\) 等概率随机，也可以跳过，求形成的序列递增的方案数。

先考虑这题。

首先将区间离散化成若干个左闭右开的区间。

设 \(f_{i, j}\) 表示考虑到 \(a_i\)，\(a_i\) 在第 \(j\) 个区间内的方案数。

枚举上一个在 \(j\) 之前的位置 \(a_k\) 转移。

设 \(k + 1 \sim i\) 中有 \(c\) 个位置可以选择第 \(j\) 个区间，设第 \(j\) 个区间的长度为 \(l_j\)，则方案数为 \(\binom{l_j + c}{c}\)。

需要前缀和优化，时间复杂度 \(\mathcal O(n^3)\)。

const int N = 507;
int n, a[N], b[N], c[N*2], t;
modint f[N], g[N], ans;

int main() {
	rd(n);
	for (int i = 1; i <= n; i++)
		rd(a[i]), rd(b[i]), c[++t] = a[i], c[++t] = ++b[i];
	sort(c + 1, c + t + 1), t = unique(c + 1, c + t + 1) - (c + 1);
	for (int i = 1; i <= n; i++)
		a[i] = lower_bound(c + 1, c + t + 1, a[i]) - c,
		b[i] = lower_bound(c + 1, c + t + 1, b[i]) - c;
	f[0] = 1;
	for (int j = 1; j < t; j++) {
		int l = c[j+1] - c[j];
		g[0] = 1;
		for (int i = 1; i <= n; i++) g[i] = g[i-1] * (l + i - 1) / i;
		for (int i = n; i; i--)
			if (a[i] <= j && j < b[i])
				for (int c = 1, k = i - 1; ~k; k--) {
					f[i] += g[c] * f[k];
					if (a[k] <= j && j < b[k]) ++c;
				}
	}
	for (int i = 1; i <= n; i++) ans += f[i];
	print(ans);
	return 0;
}

再来看原题就很简单了，照着做即可。两个限制的修改但是代码等价，有点神奇。

const int N = 57;
int n, a[N], b[N], c[N*2], t;
modint f[N], g[N], ans;

int main() {
	rd(n);
	for (int i = 1; i <= n; i++)
		rd(a[i]), rd(b[i]), c[++t] = a[i], c[++t] = ++b[i];
	sort(c + 1, c + t + 1), t = unique(c + 1, c + t + 1) - (c + 1);
	for (int i = 1; i <= n; i++)
		a[i] = lower_bound(c + 1, c + t + 1, a[i]) - c,
		b[i] = lower_bound(c + 1, c + t + 1, b[i]) - c;
	f[0] = 1;
	for (int j = t - 1; j; j--) {
		int l = c[j+1] - c[j];
		g[0] = 1;
		for (int i = 1; i <= n; i++) g[i] = g[i-1] * (l + i - 1) / i;
		for (int i = n; i; i--)
			if (a[i] <= j && j < b[i])
				for (int c = 1, k = i - 1; ~k; k--, ++c) {
					f[i] += g[c] * f[k];
					if (a[k] > j || j >= b[k]) break;
				}
	}
	ans = f[n];
	for (int i = 1; i <= n; i++) ans /= c[b[i]] - c[a[i]];
	print(ans);
	return 0;
}

ABC158E

遇到神题了。

思路

首先发现一个事情，任意一个子串都可以由 \(s\) 的某一个后缀的后面删除一些字符得到。

因此假如 \(s\) 的某一个后缀的值为 \(x\)，那么我们可以减去后面的我们不用的数字 \(a\)，然后除以 \(10\) 的若干次幂得到，即 \(\frac{x - a}{10^n}\)。

于是得到：

\[\frac{x - a}{10^n} \equiv 0 \pmod p \]

可以推出：

\[x \equiv a \pmod p \]

因此考虑处理后缀模 \(p\) 的结果，同时用桶存起来即可。

注意到有可能 \(a\) 比 \(x\) 大的情况，因此需要把这种情况删掉；同时注意到当 \(p = 2/5\) 时，\(\frac{x - a}{10^n} \bmod p\) 不存在（因为 \(10\) 与 \(p\) 不互质了），需要特殊处理。

CF1750F

很厉害的 DP 啊！感觉难点在于状态设计。

首先注意到我们的合并方式一定是这样的：每次选择相邻两段极长的 \(1\)，然后合并。注意到如果相邻的两端无法合并，那么跨过它们的也一定无法直接合并。

也就是说，如果一个序列不合法，那么当不可合并时序列一定长这样：序列能被分为 \(2k+1\) 段，其中有 \(k+1\) 段能被变为全 \(1\)，中间穿插排布着 \(k\) 段 \(0\)，且设一段 \(0\) 长度为 \(b\)，两端的 \(1\) 长度为 \(a,c\)，则必有 \(b>a+c\)。

那么考虑如何刻画这样的序列。现在就很容易想到状态 \(f_{i,j}\) 表示前 \(i\) 个位置中，最后一段连续 \(1\) 长度为 \(j\) 的方案数。满足条件的序列即为 \(f_{i,i}\)。

对于 \(i=j\) 的情况，我们可以容斥求出来。首先总序列数为除掉两边的 \(1\) 外中间随便选，即 \(2^{i-2}\)。然后再去除中间的，即

\(f_{i,i}=2^{i-2}-\sum\limits_{j=1}^{i-1}f_{i,j}\)

然后考虑 \(j<i\) 的转移。直接枚举上一段 \(0\) 和上上段 \(1\) 的长度 \(p,q\)。则有

\(f_{i,j}=f_{j,j}\sum\limits_{p,q}f_{i-j-p,q}[p+q+j\le i][p\ge j+q+1]\)

首先第一个限制可以去掉，因为 \(f_{i-j-p,q}\) 存在的前提就是 \(p+q+j\le i\)。而后面一个条件可以变成 \(p-q\ge j+1\)，化为两维和的形式就是 \((i-j-p)+q\le i-2j-1\)。

也就是说，只要维护一个数组 \(g_{k}\) 表示两维和 \(\le k\) 的 \(f\) 之和，就能 \(O(1)\) 转移。

总复杂度成功变为 \(O(n^2)\)。代码。