构造专练2
https://www.luogu.com.cn/problem/CF1214H
小思维+corner
考虑怎么染色,先找到直径,直径肯定是轮换染色,然后找到中心,
拉出来相同 dep 染一个颜色就行,这样如果寄了肯定无解了。
https://www.luogu.com.cn/problem/CF1365G
二进制性质+分组优化
先考虑二进制分组,原理是任意两个不同的数一定至少有一位二进制不同,但是这样询问次数多了。
考虑怎么优化,发现如果对于每个数,存在一定有一位这个数为 \(0\) 时,其他数字会为 \(1\)。
这样的话每个二进制位就只用访问一次了。
考虑直接构造把每个数换成二进制在 \(13\) 位下二进制位有 \(6\) 个位 \(1\) 的就好了因为 \(1\) 的次数 > \(0\) 的次数。
https://www.luogu.com.cn/problem/CF1379E
使用上下界构造并结合+分讨
祖先关系还是比较好构造的,考虑两种极限情况,一种长链每个节点多拉一个儿子,另一种是线段树。
然后直接组合就可以了,因为第二种没有个数限制,而第一种有一点。有一些corner,比如 \(n=9,k=2\) 无解。
https://www.luogu.com.cn/problem/CF1383D
矩阵填数+队列辅助构造
好题,考虑怎么样保留原始 \(S\) 中的数,那就是从大到小,每放一个就往自己原来是行还是列上移动一下。
考虑如何满足先增后降的性质,考虑从填的这个数的左侧和上侧一次从从右到左,从下到上,
大到小填数,想象一下就知道了肯定满足。
https://www.luogu.com.cn/problem/CF1491F
思考磁极性质 + 构造方案+观察
考虑先找到一个有磁极的磁铁,然后把这个磁铁一一匹配。
这时我们发现找到第一个有磁极的磁铁很有难度,因为要用到后面,所以我们找第二个有磁极的磁铁。
我们每次查询 \(1\to i\) 和 \(i+1\) 就可以知道 \(i+1\) 是不是第二个有磁极的磁铁了。
然后我们可以和后面每个磁铁一一匹配找到后面的磁铁是不是有磁极的磁铁。这两步加起来用了 \(n-1\) 次。
发现 \([1,i]\) 只有一个有磁极的磁铁,考虑二分,然后就做完了。
https://www.luogu.com.cn/problem/CF1491G
建图+环融合处理+corner case
挺好一道题,先套路性自己的位置和自己的大小连边,形成很多个简单环。
考虑没有翻转怎么做,就是一个点交换一圈这样就好了,如图:
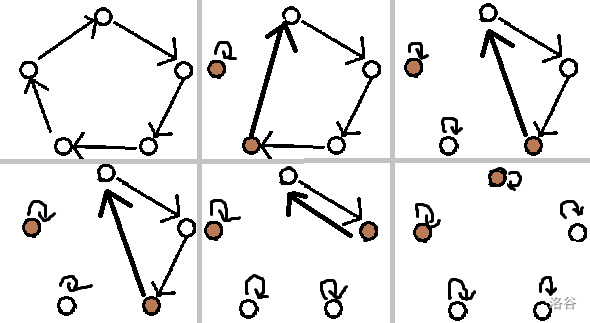
考虑加了翻转,我们发现一个环要能直接删干净要有两个背面的点,如图:
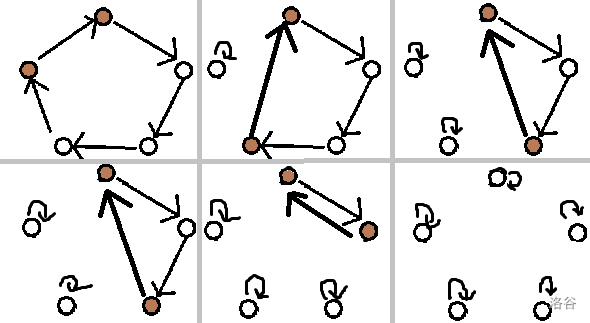
发现环内无法自己解决,考虑将两个环内两点交换,这样就有两个背面了,接下来是 corner。
如果只有一个环,最后一个环可以用 \(size+1\) 步做完。
考虑先交换两个环上相邻点,形成一个背面自环和一个带一个背面点的环。
再把这个自环和一个环上正面点交换,这样就有两个背面的环了。
如果是 \(>1\) 个环且有奇数个环,考虑直接交换一个正面自环和环上一点,产生 两个背面的环了。
分成两种 corner 的原因是第二种环长可能为 \(2\)。
https://www.luogu.com.cn/problem/CF991F
大分讨+时间复杂度分析
考虑任意一种情况都是 \(a\times b+c\) 其中 \(a,b,c\) 都是 \(X^Y\) 或者 \(X\) 或者无的形式,复杂度是对的直接分讨。
https://www.luogu.com.cn/problem/CF1477D
图上补图构造+性质
先减少限制然后转化为补图,最后构造一种合法方案(菊花),我认为十分困难。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号