#P13586 [NWRRC 2023] First Solved, Last Coded

题意：

给一个长度为 \(n\) 的入栈序列 \(a\)，问能否产生出栈序列 \(b\)，若可以请给出一种方案。

数据范围：\(1\le n\le 100\)。

题解：

看到 \(n\) 这么小先想到 dp，接下来就是确定要用什么种类的 dp。

我们从 \(a\) 中的第一个数下手，假设这个数在 \(b\) 中的第 \(k\) 个位置，那么 \(a\) 和 \(b\) 有如下对应关系。

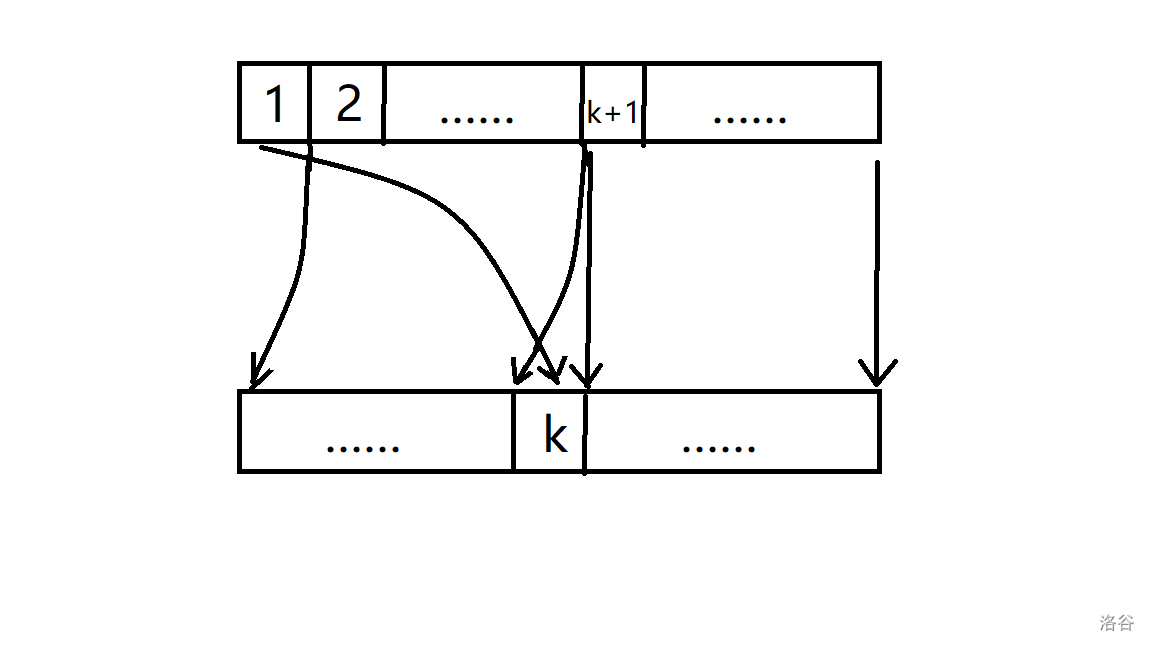
其中：

• \(a\) 中第一个数匹配 \(b\) 中第 \(k\) 个数。
• \(a\) 中第 \(2\to k\) 个数匹配 \(b\) 中第 \(1\to k-1\) 个数。
• \(a\) 中第 \(k+1\to n\) 个数匹配 \(b\) 中第 \(k+1\to n\) 个数。

为什么呢，应为 \(a\) 中一号元素出栈时必定栈只有这一个元素了，所以其前边的元素都要退栈。自然分成两个区间了。

接下来就很明显了，区间 dp。我们设 \(f_{i,j,k}\) 为从 \(a_i\) 和 \(b_j\) 开始匹配 \(k\) 位，是否能匹配上。那么答案就是 \(f_{1,1,n}\)。

考虑递归做这个事情，那么要使得 \(f_{i,j,len}\) 为真，需要同时满足如下条件：

存在一个 \(k\in [1,len]\)，使得其满足。

• \(a_i=b_{j+k-1}\)
• \(f_{i+1,j,k-1}=1\)
• \(f_{i+k,j+k,len-k}=1\)

考虑时间复杂度：状态数 \(O(n^3)\) 转移要枚举 \(k\) 所以是 \(O(n)\) 的，总时间复杂度是 \(O(n^4)\) 的。

接下来考虑怎么输出答案，考虑继续用递归，对于一种可行的转移，我们先把第一位放进去，即为输出一个 \(S\),然后递归第一部分。弹出第一位，也就是输出一个 \(C\)，接着递归第二部分，最后直接 break，不用再找第二个方案了。

code：

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
using namespace std;
const int N=110;
int n,m,k,T,a[N],f[N][N][N],b[N];
int dfs(int x,int y,int l){
	if(l<=0) return 1;
	if(f[x][y][l]!=-1) return f[x][y][l];
	if(l==1){
		if(a[x]==b[y]) f[x][y][l]=1;
		else f[x][y][l]=0;
		return f[x][y][l];
	}int ans=0;
	rep(k,1,l){
		if(a[x]!=b[y+k-1]) continue;
		ans|=(dfs(x+1,y,k-1)&dfs(x+k,y+k,l-k));
	}return f[x][y][l]=ans;
}
void solve(int x,int y,int l){
	if(l<=0) return;
	if(l==1){
		cout<<"S"<<"C";return;
	}rep(k,1,l){
		if(a[x]!=b[y+k-1]) continue;
		if(f[x+1][y][k-1]&f[x+k][y+k][l-k]){
			cout<<"S";solve(x+1,y,k-1);cout<<"C";solve(x+k,y+k,l-k);
			return;
		}
	}
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	rep(i,1,n) cin>>a[i];
	rep(i,1,n) cin>>b[i];
    memset(f,-1,sizeof(f));
    if(dfs(1,1,n)){
    	cout<<"YES\n";
    	solve(1,1,n);
	}else cout<<"NO";
	return 0;
}