CSP-S训练赛（2025.9.4）

t1 骑行

运气比较好，想到了 kruskal重构树，然后就想到了从小到大枚举点，然后计算贡献，这下就简单了（主要是做过类似的题也是先对点排序然后计算相邻点贡献，那道题是对联通快做主席树然后线段树合并做这道题）。

t2 有向图删点

比较巧妙，我们把所有点拍到序列上，一个点会被计入贡献当且仅当其所有的祖先都在他的后面，那我们也可以算出来每个点被计入答案的概率就是祖先个数的倒数，我们记作 \(p_i\)。而答案就是 \(\sum p_i\)。

我们发现计算祖先可以用传递闭包来算 \(O(\large\frac{n^3}{w})\)。

code:

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e3+10,mod=998244353;
int n,ans,ni[N];
bitset<N> T[N];
signed main(){
	freopen("graph.in","r",stdin);
	freopen("graph.out","w",stdout);
	cin>>n;ni[1]=1;
	for(int i=2;i<N;i++) ni[i]=(-mod/i*ni[mod%i]%mod+mod)%mod;
	for(int i=1;i<=n;i++){
		string s;cin>>s;
		for(int j=0;j<n;j++){
			if(s[j]=='1') T[i].set(j+1);
		}
		T[i].set(i);
	}
	for(int j=1;j<=n;j++){
		for(int i=1;i<=n;i++) if(T[i][j]) T[i]|=T[j];
	}
	for(int j=1;j<=n;j++){
		int cnt=0;
		for(int i=1;i<=n;i++) if(T[i][j]) cnt++;
		ans=(ans+ni[cnt])%mod;
	}
	cout<<ans;
	return 0;
}

t3 跑步

dp好题：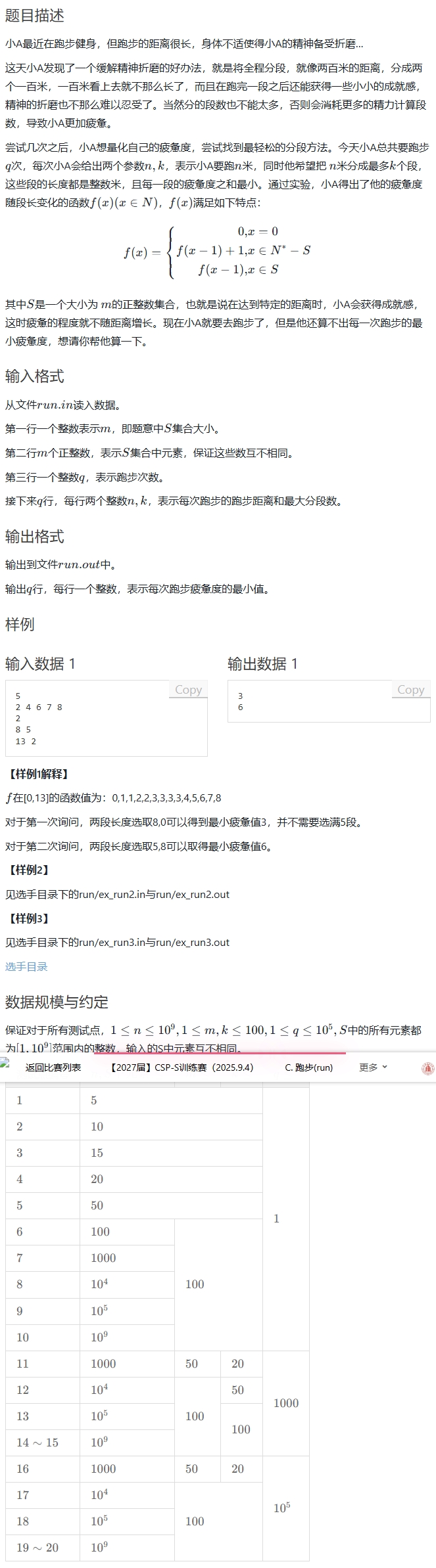

t4 数字
猎奇暴力，我就不讲这题的做法了，讲点性质。

1.这种树的树高是 \(\log\) 级别的。
2.在 \(4\times 10^4\) 下素数有 \(4\times 10^3\)，这么多个。
3.vector跑的真的很快。

t5 trip

很好的题，但是似乎只能用点分治，线段树分治/整体二分似乎都是不可做的。所以题出的很好，但是基本上用不到，贴一篇题解吧。
题目大意: 一棵树, 每条边有一个区间, 问有多少路径, 使得路径上所有区间的交集不为空。

算法 1

根据题意模拟, 枚举起终点并计算交集。

时间复杂度 \(0\left(\mathrm{n}^{3}\right)\) 。

期望得分 16 分。

算法 2

对于同一个起点, 通过一次 dfs 即可算出所有终点的答案。

时间复杂度 \(0\left(n^{2}\right)\) 。

期望得分 \(32-60\) 分。

算法 3

对于 \(r \leq 10\), 可以枚举一段区间, 然后只保留包含这段区间的所有边, 形成一些连通块, 计算路径数量。容斥即可。

时间复杂度 \(0\left(r^{2} n\right)\)

结合前面, 期望得分 \(44-64\) 分。

算法 4

对于完全二叉树的测试点, 我们先求出每个点向上跳到一个祖先的位置的过程中, 区间的交集。然后在祖先处离散化统计答案。暴力排序复杂度 \(O\left(n \log ^{2}(n)\right)\), 使用归并排序可以做到 \(O(n \log (n))\)

结合前面, 期望得分56-68分

算法 5

对于一条链的测试点, 考虑分治, 每次在中点处统计左半边到右半边的答案。同样是暴力排序复杂度 \(O\left(n \log ^{2}(n)\right)\), 使用归并排序可以做到 \(O(n \log (n))\) 。

结合前面, 期望得分 \(68-72\) 分。

算法 6

算法 5 提示了分治的做法, 不妨考虑点分治, 每次找到重心然后统计跨过重心的答案。这个就利用 dfs, 算出每个点到重心路径上道路的区间交集。比较方便的做法是先统计交集为空的情况数，这时只需要统计有多少交集区间的 \(\mathrm{l}\) 大另外的交集区间的 \(\mathrm{r}\) 。做的过程中仍然要对 \(\mathrm{l}, \mathrm{r}\) 离散化, 采用归并排序, 或者离线等方法, 可以把复杂度由 \(O\left(n \log ^{2}(n)\right)\) 降为 \(O(n \log (n))\), 但常数较大。实现良好的 \(O\left(n \log ^{2}(n)\right)\) 做法应该也可以通过。期望得分 100 分。