CSP-S训练赛（2025.9.2）

t1 分蛋糕

打表题，我用了 25 min 来发现规律，发现是组合数就写完了。

t2 膜法

这一道是原题，用插头 dp 中的经典优化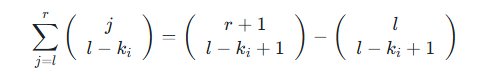
就写完了。

t3 木棍

分类讨论 分成 \(3~1~1~1\) 和 \(2~2~1~1\) 两种情况，都能枚举得到答案

t4 计数

高妙题，首先我们把限制当成一条 \(x\)，\(y\) 之间的无向边，然后发现一个点的度数只能小于等于 \(2\)，所以限制最后会形成链/环。考虑每一种形状的贡献。

• 环，让答案贡献 \(\times 2\).
• 长链（点数大于 \(2\)），答案贡献 \(\times 2\) 且创造一个可以随便放的点.
• 短链（点数为 \(2\)），答案贡献 \(\times 2\) 且创造一个可以随便放的点。但是会有重复的情况，需要容斥.
• 单点，对答案贡献一个可以随便放的点.
• 不管的单点（自己连自己）对答案没有任何贡献，直接不管。

对于容斥我们枚举 $x\to p_y $ 且 $y\to p_x $ 的个数，贡献是:

\[\sum^{n}_{i=0}(-1)^i \cdot C^{i}_{n}\cdot 2^{n-i}\cdot (k+n-i)! \]

其中 \(n\) 是短链个数，\(k\) 是单点数加上长链数。

不要忘了最后把环和长链的 \(\times 2\) 的贡献算上。
code:

#include<bits/stdc++.h>
#define pb push_back
#define int long long
using namespace std;
const int N=5e5+10,mod=998244353;
int n,m,k,T,a[N],jie[N],d[N],vis[N],mk,pw;
int del[N];
map<pair<int,int>,int> mp;
int ni[N];
int c(int n,int m){
	if(n>m) return 0;
	return jie[m]*ni[m-n]%mod*ni[n]%mod;
}
vector<int> g[N];
int ksm(int x,int k){
	int ans=1;
	while(k){
		if(k&1) ans=ans*x%mod;
		x=x*x%mod;k>>=1;
	}return ans;
}
int dfs(int u,int fa){
	vis[u]=1;int tag=2;if(d[u]==1) tag=1;
	if(fa==0&&d[u]==1&&d[g[u][0]]==1){
		vis[g[u][0]]=1;return 0;
	}for(int v:g[u]){
		if(v==fa||vis[v]) continue;
		tag=min(tag,dfs(v,u));
	}return tag;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
	cin>>n>>m;jie[0]=1;
    for(int i=1;i<N;i++) jie[i]=jie[i-1]*i%mod;
    ni[N-1]=ksm(jie[N-1],mod-2);
    for(int i=N-2;i>=0;i--){ni[i]=ni[i+1]*(i+1)%mod;}
	for(int i=1;i<=m;i++){
		int u,v;cin>>u>>v;
		if(u==v) del[u]=1;
		else if(mp[{u,v}]==0){
			d[u]++,d[v]++;
			g[u].pb(v);
			g[v].pb(u);
			if(d[u]==3||d[v]==3){
				cout<<0;return 0;
			}
		}
		mp[{u,v}]=mp[{v,u}]=1;
	}
	for(int i=1;i<=n;i++){
		if(vis[i]==0&&d[i]&&del[i]==0){
			int x=dfs(i,0);
			if(x==0) mk++;
			else if(x==1) k++,pw++; 
			else pw++;
		}
		if(del[i]==0&&d[i]==0) k++;
	}int res=0;
	for(int i=0;i<=mk;i++){
		int t=ksm(2,mk-i)*c(i,mk)%mod*jie[k+mk-i]%mod;
		if(i&1) (res-=t)%=mod; 
		else (res+=t)%=mod;
	}
	cout<<ksm(2,pw)*(res+mod)%mod;
	return 0;
}

t5 「雅礼集训 2018 Day1」图

难点在状态设计和转换，不太会先鸽了。