P12578 [UOI 2021] 彩色矩阵 题解

P12578\(\mathbf{} \begin{Bmatrix} \frac{{\Large LUOGU-P12578} }{{\color{Red}\Large Solution} }\mathbf{} {No.28} \end{Bmatrix}\times{}\) NeeDna

题意

给定一个 \(n \times m\) 的网格，即包含 \(n\) 行和 \(m\) 列。

要求不存在两个颜色相同的单元格，且它们之间的曼哈顿距离等于 \(k\)。

两个单元格 \((x_1, y_1)\) 和 \((x_2, y_2)\) 之间的曼哈顿距离为 \(|x_1 - x_2| + |y_1 - y_2|\)。

请找到所需的最少颜色数量，并输出着色后的网格。其中（\(1 \leq n, m, k \leq 100\)，\(k < \min(n, m)\)）。

题解

这道题明显是一道构造题，看一下我们如何构造它：

有一个明显的情况是：当 \(k\) 为奇数的时候黑白格子相间染色即可，颜色数量为2，因为黑白图染色后颜色相同的点距离一定为偶数。

接下来 \(k\) 为偶数怎么办，我们可以想象一下，一个点的限制是一个斜着的矩形：

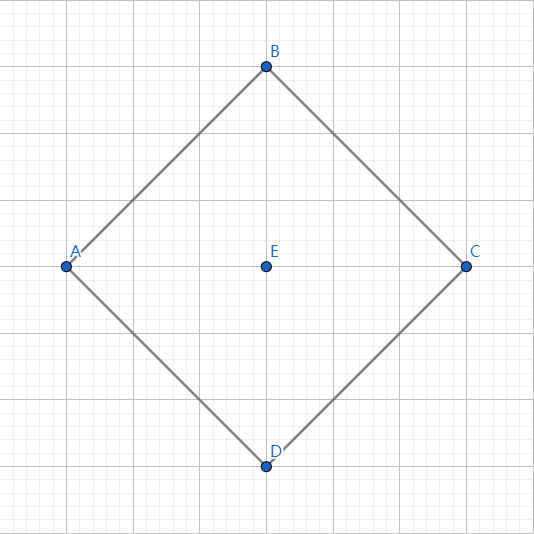
我们只需要保证这个边界上的点都和中心点不同即可。

在众多尝试以后，我们可以发现以下只需要4种颜色的构造方法：

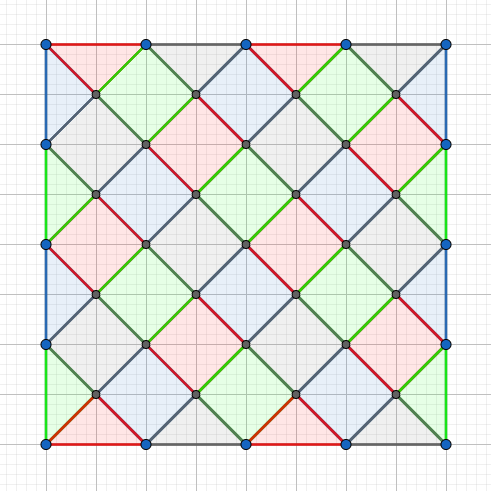
其中每个小正方形的对角线长度为 \(k\)，放在网格图上会有些边界问题，这里个大家放一个 \(k=4\) 时候的矩形来方便大家理解（由于大正方形可以拆成多个小正方形，我们只提供一个最小的单元）。

至于为什么，大家可以手玩一下，证明是显然的。代码实现估计大家都不一样，但还是贴一下代码。

code:

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m,k,cnt,mo[N][N],mp[N][N],col;
int main(){
	cin>>n>>m>>k;
	if(k%2==1){
		if(n==m&&m==1){cout<<1<<'\n'<<0;return 0;}
		cout<<2<<'\n';
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				if((i+j)%2==1) cout<<0<<" ";
				else cout<<1<<" ";
			}cout<<'\n';
		}return 0;
	}
	cout<<4<<'\n';
	for(int i=1;i<=k/2;i++){
		for(int j=1;j<=k/2;j++){
			if(i>=j) mo[i][j]=3;
		}
		for(int j=k/2+1;j<=k;j++){
			mo[i][j]=mo[i][k-j+1];
			if(mo[i][j]==3) mo[i][j]=1;
		}
	}
	for(int i=k/2+1;i<=k;i++){
		for(int j=1;j<=k/2;j++){
			mo[i][j]=mo[i-k/2][j+k/2];
			if(mo[i][j]) mo[i][j]=2;
			else mo[i][j]=3;
		}
		for(int j=k/2+1;j<=k;j++){
			mo[i][j]=mo[i-k/2][j-k/2];
			if(mo[i][j]) mo[i][j]=2;
			else mo[i][j]=1;
		}
	}
	
	for(int i=1;i<=k;i++){
		for(int j=k+1;j<=k*2;j++){
			mo[i][j]=mo[i][2*k-j+1];
			if(mo[i][j]==2) mo[i][j]=0;
			else if(mo[i][j]==0) mo[i][j]=2;
		}
	}
	for(int i=k+1;i<=2*k;i++){
		for(int j=1;j<=k;j++){
			mo[i][j]=mo[i-k][j+k];
		}
		for(int j=k+1;j<=k*2;j++){
			mo[i][j]=mo[i-k][j-k];
		}
	}//实现上述最小单元的构造
    k*=2;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cout<<mo[(i-1)%k+1][(j-1)%k+1]<<" ";
		}cout<<'\n';
	}
	return 0;
}