题解：P9433 [NAPC-#1] Stage5 - Conveyors

P9433 题解

题面

原题传送门

思路

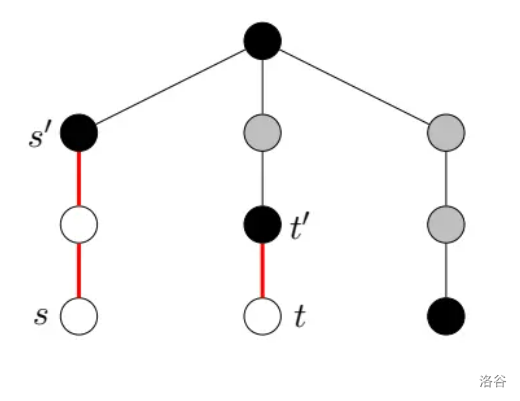
任取一个关键点作为根，这样，关键点就构成了一个包含根节点的连通块。如图中的黑色 (关键点) 和灰色部分所示。

由于关键点连通块的根就是树根，\(s\)（或 \(t\)）一定存在一个祖先 \(s'\)，使得 \(s'\) 以上的结点都在连通块内，而 \(s'\) 以下（不含 \(s'\)）到 \(s\) 的结点都不在连通块内。我们预处理出每个结点在不在关键点连通块，然后利用倍增数组向上跳跃，就能求出 \(s'\) 和 \(t'\)，如下图红色部分。

所以答案就为 \(2w-\operatorname{dis}(s',t')+\operatorname{dis}(s,s')+\operatorname{dis}(t,t')\)。

其中，\(w\) 为联通快内所有边权和。减去 \(\operatorname{dis}(s',t')\) 是因为 \(s'\) 到 \(t'\) 不用多算一遍。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
#define ll long long
using namespace std;
const int MN=1e5+5;
ll n,q,k,x,sum[MN],sz[MN],deep[MN],head[MN],tot,fa[MN][20],cnt;
bool flag[MN],vis[MN];
char buf[1<<23],*p1=buf,*p2=buf;
struct edge{ll to,nxt,w;}e[MN<<1];
void write(ll n){if(n<0){putchar('-');write(-n);return;}if(n>9)write(n/10);putchar(n%10+'0');}
ll read(){ll x=0,f=1;char ch=gc();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=gc();}return x*f;}
void add(ll u, ll v, ll w){e[++tot].nxt=head[u];head[u]=tot;e[tot].to=v;e[tot].w=w;}
void lca_dfs(ll u, ll lst){
    deep[u]=deep[lst]+1;fa[u][0]=lst;
    if(flag[u]) sz[u]=1;
    for(int i=1; i<20; i++) fa[u][i]=fa[fa[u][i-1]][i-1];
    for(int i=head[u]; i; i=e[i].nxt){
        ll v=e[i].to,w=e[i].w;
        if(v==lst) continue;
        sum[v]=sum[u]+w;
        lca_dfs(v,u);
        sz[u]+=sz[v];
    }
}
ll lca(ll x, ll y){
    if(deep[x]<deep[y]) swap(x,y);
    for(int i=19; ~i; i--) if(deep[x]-(1<<i)>=deep[y]) x=fa[x][i];
    if(x==y) return x;
    for(int i=19; ~i; i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
void dfs(ll u, ll lst){
    if(!sz[u]) return;
    vis[u]=true;
    for(int i=head[u]; i; i=e[i].nxt){
        ll v=e[i].to,w=e[i].w;
        if(v==lst) continue;
        dfs(v,u);
        if(vis[u]&&vis[v]) cnt+=w;
    }
}
ll dist(ll u, ll v){return sum[u]+sum[v]-sum[lca(u,v)]*2;}
ll getrt(ll u){
    if(vis[u]) return u;
    for(int i=19; ~i; i--) if(fa[u][i]&&!vis[fa[u][i]]) u=fa[u][i];
    return fa[u][0];
}
int main(){
    //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    n=read();q=read();k=read();
    for(int i=1; i<n; i++){
        ll u=read(),v=read(),w=read();
        add(u,v,w);add(v,u,w);
    }
    for(int i=1; i<=k; i++){x=read();flag[x]=true;}
    lca_dfs(x,0);dfs(x,0);
    while(q--){
        ll s=read(),t=read(),fs=getrt(s),ft=getrt(t);
        write(2*cnt-dist(fs,ft)+dist(s,fs)+dist(t,ft));putchar('\n');
    }
    return 0;
}//250316