P7697 题解

P7697 题解

前置知识

1. 单调队列求区间最值。（可以看后记）

题面

原题传送门

思路

第一个答案

先看样例解析图：

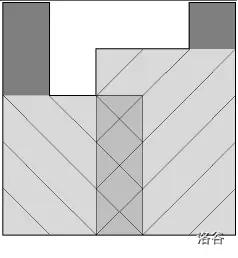
我们需要满足题目刷的限制，保证刷子完全接触栅栏，也就是每次刷的时候不能刷到空的；

所以，我们可以求得在 \(i\) 到 \(i+x-1\) 刷的高度就是 \(\min(a[j])(j\in[i,i+k-1])\)。

我们用一个数组 \(h\) 来记录这个值。

于是，两眼一瞪，就可以看出来这就是裸的单调队列求最小值嘛！简简单单的进行一次单调队列就可以求出 \(h\)。

当然，继续往下考虑，会发现，只有一个 \(h\) 这个求区间的数组远远不够，我们需要的是一个能记录每个木板能刷到的最大值。

于是再设一个数组 \(mx\) 来存每个木板能刷到的最大值。

由 \(h,mx\) 数组的定义，我们可以知道 \(mx[i]=\max(h[j])(j\in[i-k+1,i])\)。

于是又一瞪，这不又是一个单调队列求区间最大值模板吗？简简单单解决了！

于是，第一问就解决了，只要累加一下 \(a[i]-mx[i]\) 即可（原先高度减去最大能刷的高度）。

第一问代码

for(int i=1; i<=n; i++){//单调队列求最小值。
        while(head<=tail&&a[q[tail]]>a[i]) tail--;
        q[++tail]=i;
        while(head<=tail&&i-q[head]+1>x) head++;
        if(i-x+1>=0) h[i-x+1]=a[q[head]];
    }
    head=1,tail=0;
    for(int i=1; i<=n; i++){//单调队列求最大值。
        while(head<=tail&&h[q[tail]]<h[i]) tail--;
        q[++tail]=i;
        while(head<=tail&&i-q[head]+1>x) head++;
        mx[i]=h[q[head]];
    }
	for(int i=1; i<=n; i++) ans+=a[i]-mx[i];//记录第一个答案。
	printf("%lld\n",ans);

第二个答案

来到了第二问，这一看，难道是要再写一遍？？？不不不，只要求出的 \(mx\) 就足够了。有以下两种情况:

• \(i\sim i+x-1\)：如果遇到了 \(mx[i]\) 不同的情况那就是要新刷一次，重新把不同的地方当 \(i\) 来算。
• \(i\sim i+x-1\)：如果全部相同，那就新刷一次，把 \(i+x\) 当做 \(i\) 来算。

累加即可。

第二问代码

long long lst=0,nxt=0;
	for(int i=1; i<=n; i++){
		if(mx[i]!=lst||nxt<i){//长度超了或者两个不同 
			lst=mx[i];
			nxt=i+x-1;
			ans++;
		}
	}

总代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int MN=1000005;
long long n,x,a[MN],q[MN],h[MN],mx[MN],head=1,tail=0,ans;
int main(){
	scanf("%lld %lld",&n,&x);
	for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
	for(int i=1; i<=n; i++){//单调队列求最小值。
        while(head<=tail&&a[q[tail]]>a[i]) tail--;
        q[++tail]=i;
        while(head<=tail&&i-q[head]+1>x) head++;
        if(i-x+1>=0) h[i-x+1]=a[q[head]];
    }
    head=1,tail=0;//初始化。
    for(int i=1; i<=n; i++){//单调队列求最大值。
        while(head<=tail&&h[q[tail]]<h[i]) tail--;
        q[++tail]=i;
        while(head<=tail&&i-q[head]+1>x) head++;
        mx[i]=h[q[head]];
    }
	for(int i=1; i<=n; i++) ans+=a[i]-mx[i];//记录第一个答案。
	printf("%lld\n",ans);
	ans=0;//初始化。
	long long lst=0,nxt=0;
	for(int i=1; i<=n; i++){
		if(mx[i]!=lst||nxt<i){
			lst=mx[i];
			nxt=i+x-1;
			ans++;
		}
	}
    printf("%lld\n",ans);
	return 0;
}

后记

这是到练单调队列的好题，当然，你翻到这可能是你不咋了解单调队列，那我也来讲解一下吧。

问题引入

单调队列模板题

算法介绍

队列大家应该都知道，那单调队列单调队列，顾名思义就是要保持元素的单调性的队列。

算法流程

其实由介绍就可以知道代码大概要怎么写了，我也不多说，会模拟的可以先自己去尝试尝试，实在不行，请自行理解下面的代码：

//求最小值，最大值同理，代码不放，要自行思考才能完全理解这个算法 
head=1;tail=0;//为啥要这样呢?因为head要严格对应首元素，tail要严格对应尾元素，所以当tail>=head时，说明有元素。而一开始队列为空，说一要这样赋值。其实这跟普通队列一样。
for(int i=1; i<=n; i++){//a[i]表示当前要处理的值
    while(head<=tail&&q[tail]>=a[i]) tail--;//只要队列里有元素，并且尾元素比待处理值大，即表示尾元素已经不可能出场，所以出队。直到尾元素小于待处理值，满足"单调"。
    q[++tail]=a[i];//待处理值入队。
    p[tail]=i;//同时存下其编号
    while(p[head]<=i-k) head++;//如果队首元素已经"过时"，出队。
    if(i>=k) printf("%d ",q[head]);//输出最值，即队首元素。i>=k表示该输出，至于why就自己看题目。
}

题目迁移

好消息，坏消息（值得一做的单调队列训练题）