Games 101: 旋转矩阵

旋转矩阵

本文主要介绍了旋转矩阵的推导，分为两种方式：

• 旋转坐标
• 旋转坐标轴
  以下坐标系都是右手坐标系

旋转坐标

已知坐标点\(A(x_a,y_a)\), 旋转\(\theta\)角后变为坐标点\(B(x_b,y_b)\),求解旋转矩阵.

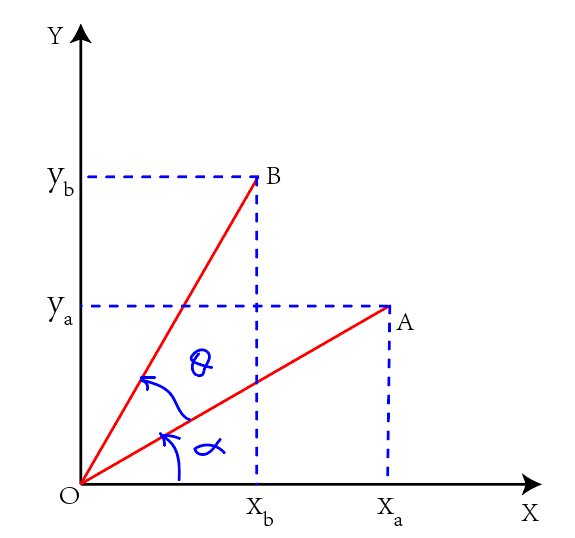
\[{\large \begin{align*} \begin{split} x_a &=r_a \cdot cos(\alpha) =r_b \cdot cos(\alpha) \\ y_a &=r_a \cdot sin(\alpha) =r_b \cdot sin(\alpha) \\ x_b &=r_b \cdot cos(\alpha+\theta) \\ &=r_b \cdot cos(\alpha) \cdot cos(\theta)-r_b \cdot sin(\alpha) \cdot sin(\theta) \\ &=x_a \cdot cos(\theta) - y_a \cdot sin(\theta) \\ y_b &=r_b \cdot sin(\alpha+\theta) \\ &=r_b \cdot cos(\alpha) \cdot sin(\theta)+r_b \cdot sin(\alpha) \cdot cos(\theta) \\ &=x_a \cdot sin(\theta) + y_a \cdot cos(\theta) \end{split} \end{align*} } \]

即：

\[{\large \begin{align*} \begin{split} \begin{bmatrix} x_b \\ y_b \\ \end{bmatrix} =\begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix} \cdot \begin{bmatrix} x_a \\ y_a \\ \end{bmatrix} \end{split} \end{align*} } \]

推广到三维以及其他轴，可以得到三维坐标点的旋转矩阵为：

\[{\large \begin{align*} \begin{split} R_x(\alpha)= \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha) & -sin(\alpha) \\ 0 & sin(\alpha) & cos(\alpha) \\ \end{bmatrix} \qquad R_y(\beta)= \begin{bmatrix} cos(\beta) & 0 & sin(\beta)\\ 0 & 1 & 0 \\ -sin(\beta) & 0 & cos(\beta) \\ \end{bmatrix} \qquad R_z(\theta)= \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split} \end{align*} } \]

旋转坐标

坐标轴\(OX_1Y_1\)绕z轴旋转\(\theta\)角后变为坐标轴\(OX_2Y_2\)，点A在坐标轴\(OX_1Y_1\)中坐标为\((x_a,y_a)\)， 在坐标轴\(OX_2Y_2\)中\((x_b,y_b)\),求解旋转矩阵.
坐标轴\(OX_1Y_1\),两个方向的单位向量为\(\vec{x_1},\vec{y_1}\)，坐标轴\(OX_2Y_2\),两个方向的单位向量为\(\vec{x_2},\vec{y_2}\)

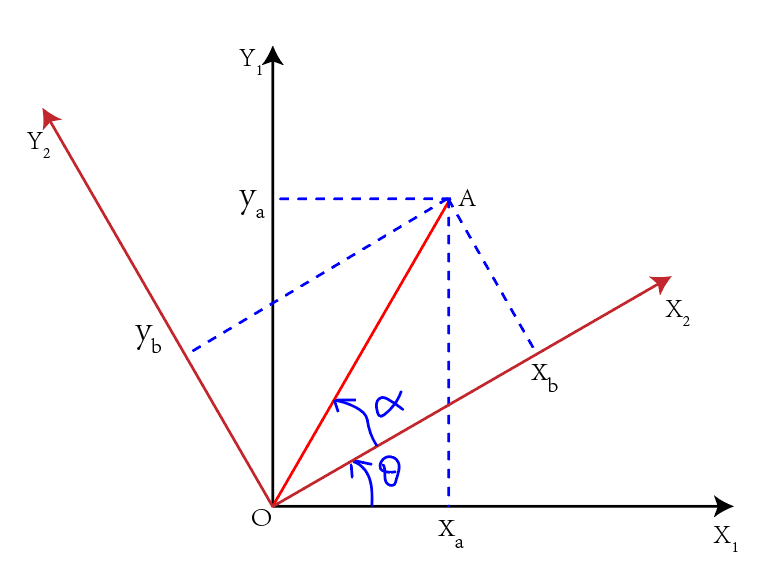
分解单位向量：

\[{\large \begin{align*} \begin{split} \vec{x_1} &=\left | \vec{x_1} \right | \cdot cos(\theta) \cdot \vec{x_2} - \left | \vec{x_1} \right | \cdot sin(\theta) \cdot \vec{y_2} = cos(\theta) \cdot \vec{x_2} - sin(\theta) \cdot \vec{y_2} \\ \vec{y_1} &=\left | \vec{y_1} \right | \cdot sin(\theta) \cdot \vec{x_2} + \left | \vec{x_1} \right | \cdot cos(\theta) \cdot \vec{y_2} = sin(\theta) \cdot \vec{x_2} + cos(\theta) \cdot \vec{y_2} \end{split} \end{align*} } \]

向量变换：

\[{\large \begin{align*} \begin{split} \vec{r_a} &= x_a \cdot \vec{x_1} + y_a \cdot \vec{y_1} \\ &= x_a \cdot ( cos(\theta) \cdot \vec{x_2} - sin(\theta) \cdot \vec{y_2}) + y_a \cdot ( sin(\theta) \cdot \vec{x_2} + cos(\theta) \cdot \vec{y_2})\\ &=(x_a \cdot cos(\theta) +y_a \cdot sin(\theta)) \cdot \vec{x_2} +(-sin(\theta) \cdot x_a + cos(\theta) \cdot y_a)\cdot \vec{y_2} \\ \vec{r_a} &= x_b \cdot \vec{x_2} + y_b \cdot \vec{y_2} \end{split} \end{align*} } \]

即

\[{\large \begin{align*} \begin{split} \begin{bmatrix} x_b \\ y_b \end{bmatrix} =\begin{bmatrix} cos(\theta) & sin(\theta)\\ -sin(\theta) & cos(\theta) \end{bmatrix} \cdot \begin{bmatrix} x_a \\ y_a \end{bmatrix} \end{split} \end{align*} } \]

推广到三维以及其他轴，可以得到三维坐标轴的旋转矩阵为：

\[{\large \begin{align*} \begin{split} R_x(\alpha)= \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha) & sin(\alpha) \\ 0 & -sin(\alpha) & cos(\alpha) \\ \end{bmatrix} \qquad R_y(\beta)= \begin{bmatrix} cos(\beta) & 0 & -sin(\beta)\\ 0 & 1 & 0 \\ sin(\beta) & 0 & cos(\beta) \\ \end{bmatrix} \qquad R_z(\theta)= \begin{bmatrix} cos(\theta) & sin(\theta) & 0 \\ -sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split} \end{align*} } \]