Games 101: 透视插值

透视插值

本文主要讨论图形学中三角形重心插值相关内容，主要涉及：

1. 重心坐标
2. 透视插值

重心坐标

在图形学中，重心坐标是用来根据三角形三个顶点属性，插值计算三角形内部任意一点的属性值。如下图：

对于三角形内任意一点\(P(x_p,y_p)\),求解\(\alpha, \beta, \gamma\),使得\(P=\alpha \cdot A + \beta \cdot B + （1-\alpha -\beta) \cdot C\),则可得方程：

\[{\large \begin{align*} \begin{split} x_p &=\alpha \cdot x_a +\beta \cdot x_b + (1-\alpha-\beta) \cdot x_c \\ y_p &=\alpha \cdot y_a +\beta \cdot y_b + (1-\alpha-\beta) \cdot y_c \end{split} \end{align*} } \]

求解得:

\[{\large \begin{align*} \begin{split} \alpha & =\frac{(x_p-x_c)\cdot (y_b-y_c)-(y_p-y_c)\cdot (x_b-x_c)}{(x_a-x_c) \cdot (y_b-y_c)-(y_a-y_c)\cdot(x_b-x_c)} \\ \beta &=\frac{(x_p-x_c)\cdot (y_a-y_c)-(y_p-y_c)\cdot (x_a-x_c)}{(x_b-x_c) \cdot (y_a-y_c)-(y_b-y_c)\cdot(x_a-x_c)} \end{split} \end{align*} } \]

记\(S_A=S_{PCB}\),\(S=S_{ACB}\)有:

\[{\large \begin{align*} \begin{split} S_A &=\left | \vec{PC} \times \vec{BC} \right |=\left | (x_p-x_c)\cdot (y_b-y_c)-(y_p-y_c)\cdot (x_b-x_c) \right | \\ S &=\left | \vec{AC} \times \vec{BC} \right |=\left | (x_a-x_c) \cdot (y_b-y_c)-(y_a-y_c)\cdot(x_b-x_c)\right | \end{split} \end{align*} } \]

由于\({\large0 \leq \alpha \leq 1 }\), 所以\({\large \alpha= \left | \alpha \right |}\)即\({\large \alpha=\frac{S_A}{S}}\),
综上可以推得：

\[{\large P=\frac{S_A}{S}A+\frac{S_B}{S}B+\frac{S_C}{S}C } \]

透视插值

这一部分首先参考论文Perspective-Correct Interpolation

已知图中直线AB，A的坐标\((X_1,Z_1)\)，B的坐标\((X_2,Z_2)\)，投影到屏幕上为\(a(u_1,d)\)和\(b(u_2,d)\)，现在对于直线ab上任意一点\(c(u_s,d)\)需求原坐标点C的坐标
根据三角相似,可以推导：

\[{\large \begin{align*} \begin{split} Z_t &=\frac{d\cdot X_t}{u_s}=\frac{d(X_1+t(X_2-X_1))}{u_1+s(u_2-u_1)}=\frac{d(\frac{u_1Z_1}{d}+t(\frac{u_zZ_z}{d}-\frac{u_1Z_1}{d}))}{u_1+s(u_2-u_1)}=\frac{u_1Z_1+t(u_2Z_2-u_1Z_1)}{u_1+s(u_2-u_1)} \\ Z_t &=Z_1+t(Z_2-Z_1) \end{split} \end{align*} } \]

求解得到

\[t=\frac{sZ_1}{sZ_1+(1-s)Z_2} \]

则可以得到：

\[\begin{align*} \begin{split} X_t &=X_1+\frac{sX_1}{sX_1+(1-s)X_2}(X_2-X_1) \\ Z_t &=Z_1+\frac{sZ_1}{sZ_1+(1-s)Z_2}(Z_2-Z_1) \end{split} \end{align*} \]

化简得到：

\[{\large \begin{align*} \begin{split} X_t &= \frac{1}{\frac{1}{X_1}+s(\frac{1}{X_2}-\frac{1}{X_1})} \\ Z_t &= \frac{1}{\frac{1}{Z_1}+s(\frac{1}{Z_2}-\frac{1}{Z_1})} \\ \end{split} \end{align*} } \]

对于任意直线上，已知点A、B的属性\(I_1,I_2\)，插值点的属性应该为

\[{\large I_t=I_1+t(I_2-I_1)=\frac{\frac{I_1}{Z_1}+s(\frac{I_2}{Z_2}-\frac{I_1}{Z_1})}{\frac{1}{Z_1}+s(\frac{1}{Z_2}-\frac{1}{Z_2})}=\frac{\frac{I_1}{Z_1}+s(\frac{I_2}{Z_2}-\frac{I_1}{Z_1})}{\frac{1}{Z_t}} } \]

即下列等式成立：

\[{\large \begin{align*} \begin{split} \frac{I_t}{Z_t}=\frac{I_1}{Z_1}+s(\frac{I_2}{Z_2}-\frac{I_1}{Z_1}) \\ \frac{I_t}{Z_t}=(1-s)\frac{I_1}{Z_1}+s\frac{I_2}{Z_2} \end{split} \end{align*} } \]

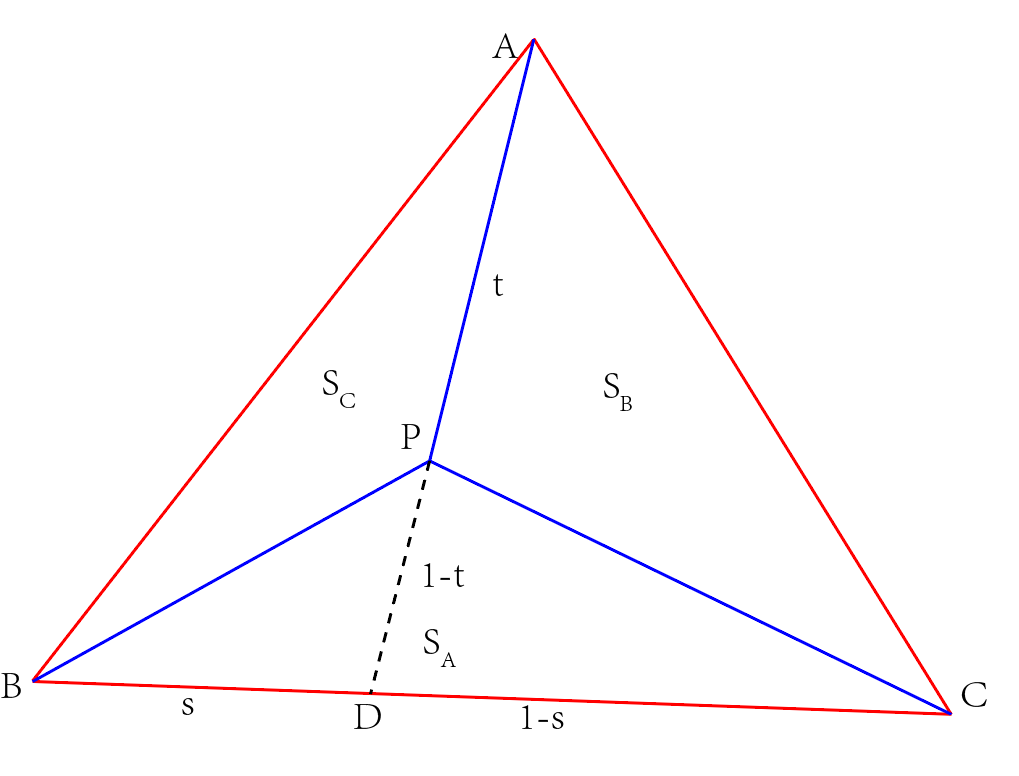
在渲染三角形时，需要根据三角形三个顶点的属性确认内部某一个点的属性。

如上图，根据三角形同底等高，有\({\large \frac{S_{PDB}}{S_{PDC}}=\frac{S_C}{S_B}}\),则

\[{\large \begin{align*} \begin{split} S_{PDB}=\frac{S_C}{S_B+S_C} \cdot S_A \\ S_{PDC}=\frac{S_B}{S_B+S_C} \cdot S_A \end{split} \end{align*} } \]

可以推导：

\[{\large \begin{align*} \begin{split} X_P-X_A&=t(X_D-X_A) \\ t&=\frac{X_P-X_A}{X_D-X_A}=\frac{PA}{AD}=\frac{S_C}{S_C+S_{PDB}}=\frac{S_B+S_C}{S_A+S_B+S_C} \\ X_D-X_B &=s(X_C-X_B) \\ s&= \frac{X_D-X_B}{X_C-X_B}=\frac{BD}{BC}=\frac{S_{PDB}}{S_A}=\frac{S_C}{S_B+S_C} \end{split} \end{align*} } \]

综上：

\[{\large \begin{align*} \begin{split} \frac{I_P}{Z_P}&=(1-t)\frac{I_A}{Z_A}+t\frac{I_D}{Z_D} \\ &=(1-t)\frac{I_A}{Z_A} +t((1-s)\frac{I_B}{Z_B}+s\frac{I_C}{Z_C}) \\ &=(1-t)\frac{I_A}{Z_A} +t(1-s)\frac{I_B}{Z_B}+ts\frac{I_C}{Z_C} \\ &=\frac{S_A}{S}\cdot \frac{I_A}{Z_A}+\frac{S_B}{S}\cdot \frac{I_B}{Z_B}+\frac{S_C}{S}\cdot \frac{I_C}{Z_C} \end{split} \end{align*} } \]