Games 101: 投影矩阵

Overview

本文主要讨论投影矩阵相关问题，主要涉及：

1. 基本变换
2. 正射投影
3. 透视投影

基本变换

绕坐标轴旋转：

\[R_x= \begin{bmatrix} 1 & 0 & 0 &0 \\ 0 & cos(\alpha) & -sin(\alpha) & 0 \\ 0 & sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \qquad R_y= \begin{bmatrix} cos(\alpha) & 0 & sin(\alpha) &0 \\ 0 & 1 & 0 & 0 \\ -sin(\alpha) & 0 & cos(\alpha) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \qquad R_z= \begin{bmatrix} cos(\alpha) & -sin(\alpha) & 0 & 0 \\ sin(\alpha) & cos(\alpha) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

缩放：

\[S(s_x,s_y,s_z)= \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

*行移动：

\[T(t_x,t_y,t_z)= \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

正射投影

正射投影是将长方体\([l,r] \times [b,t] \times [f,n]\) 映射为NDC标准立方体$[-1,1] \times [-1,1] \times [-1,1] $ 先将长方体中心*移到原点，然后缩放，得到投影矩阵

\[{\Large M_{ortho}= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} } \]

透视投影

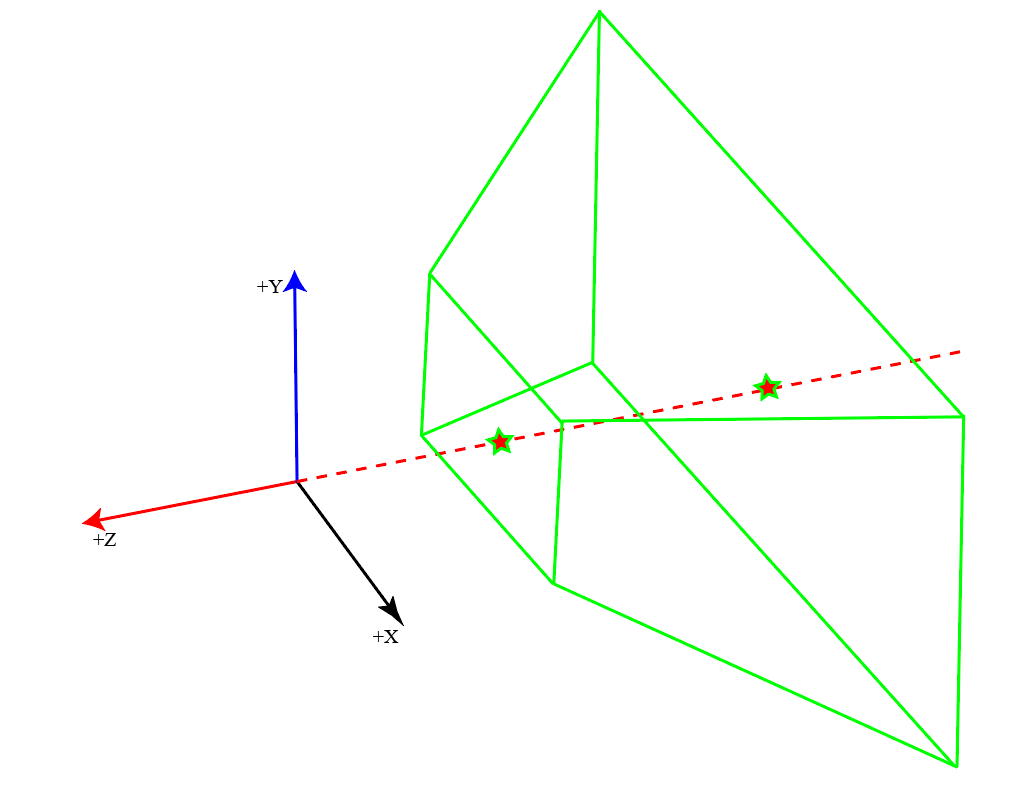
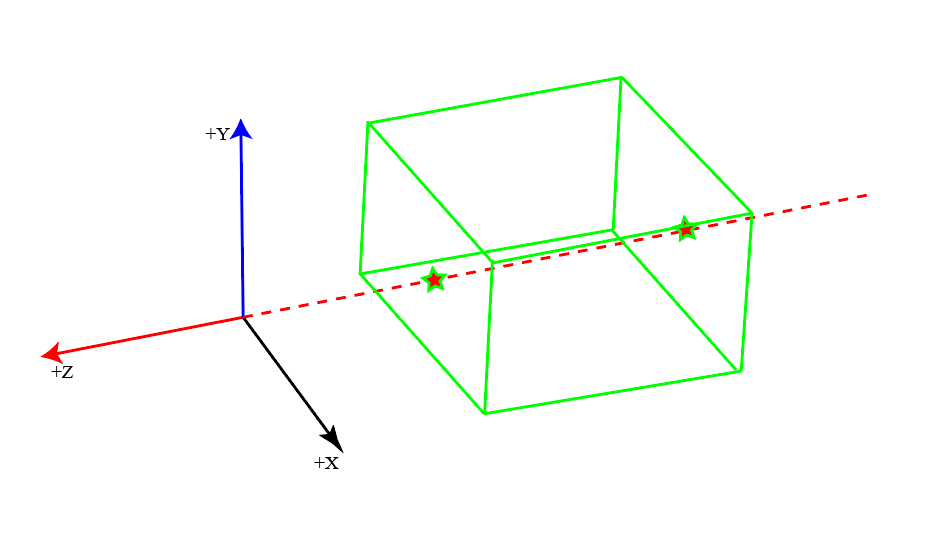
正射投影是将视椎体\([l,r] \times [b,t] \times [f,n]\) 映射为NDC标准立方体$[-1,1] \times [-1,1] \times [-1,1] $ ，先将视椎体压缩为长方体，如下左图变换为右图，然后根据乘以正射投影矩阵，即可得到NDC标准立方体。
注意：视椎体顶点为原点，关于XOZ和YOZ*面轴对称

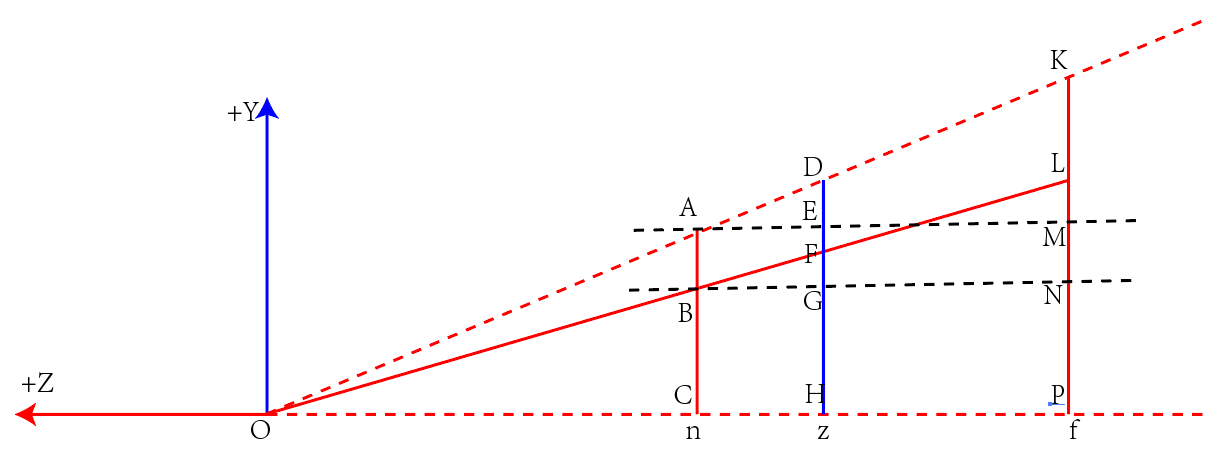
下面讨论将视椎体压缩为长方体，在YOZ*面中,梯形ACPK被压缩为长方形ACPM，如下图所示。

椎体中AK被压缩为长方体中AM. 默认成比例线性压缩(此处不清楚具体原因)，则对于椎体KP上任意一点L，求解其被压缩后的点R,则有

\[{\large \frac{PR}{PL}=\frac{MP}{KP}=\frac{AC}{KP}=\frac{n}{f}=\frac{BC}{PL}=\frac{PN}{PL}} \]

所以压缩后的点R与N点重合,故直线BL压缩为直线BN.
对直线BL上任意坐标点\(F(z_f,y_f)\),压缩后的点必然位于BN上，即任意点\(F\)的纵坐标\(y_f\)压缩为\(y_b\),根据几何相似可得：

\[y_b=\frac{y_f}{z_f} \cdot n \]

同理映射x方向，则映射关系为：

\[\begin{bmatrix} x_f \\ y_f \\ z_f \\ 1\\ \end{bmatrix} -> \begin{bmatrix} \frac{x_f}{z_f} \cdot n \\ \frac{y_f}{z_f} \cdot n \\ unknown \\ 1\\ \end{bmatrix} -> \begin{bmatrix} n \cdot x_f\\ n \cdot y_f \\ unknown \\ z_f\\ \end{bmatrix} \]

压缩矩阵为：

\[ proj= \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & o \\ A_x & B_x & C_x & D_x \\ 0 & 0 & 1 & 0 \end{bmatrix} \]

下面求解第三行的未知数，可以根据以下两个条件求得：

1. **面的坐标点在压缩后不变
2. 远*面的坐标点z方向在压缩后不变

对于条件1,*处*面任一点\(proj \cdot (x,y,n,1)^T=(nx,ny,n^2,n)^T\) ,对任意\((x,y)\)有以下方程成立

\[A_x \cdot x+ B_x \cdot y + C_x \cdot n +D_x \cdot 1 =n^2 \]

可得\(A_x=B_x=0 \quad C_x \cdot n +D_x=n^2\)
注意：对于齐次坐标\((x,y,n,1)^T、(nx,ny,n^2,n)\) 为同一个点
对于条件2：远*面任意一点\(proj \cdot (x,y,f,1)^T=(fx,fy,f^2,f)^T\),则有：

\[C_x \cdot f +D_x \cdot 1 =f^2 \]

联立条件1，可得：
\(C_x=n+f \qquad D_x=-nf\)

综上所述压缩矩阵为：

压缩矩阵为：

\[ proj= \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{bmatrix} \]

透视投影矩阵为

\[{\large \begin{align*} \begin{split} M_{proj}&=M_{ortho} \cdot proj= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{bmatrix} \\ &=\begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{n+f}{n-f} & -\frac{2nf}{n-f} \\ 0 & 0 & 1 & 0 \end{bmatrix} \end{split} \end{align*} } \]