Games 101：绕任意轴旋转

Overview

对于任意坐标\(S_1=(S_x,S_y,S_z)^T\),绕任意轴线\(\vec{n}=(n_x,n_y,n_z)^T\)旋转\(\alpha\)度，推导变换矩阵\(R(\vec{n},\alpha)\)，使得变换后的坐标\(S_2=R(\vec{n},\alpha) \cdot S_1\)
本文使用向量运算，推导该变换矩阵。 注意：轴线经过坐标系原点

基本公式

以列向量表示坐标，将向量乘法转换为矩阵乘法：

对于两个向量点乘：

\[\vec{a} \cdot \vec{b}=a_x\cdot b_x +a_y\cdot b_y +a_z\cdot b_z=\begin{bmatrix} a_x & a_y & a_z \\ \end{bmatrix} \cdot \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix} =A^T \cdot B \]

对于三个向量点乘：

\[\vec{a} \cdot \vec{b} \cdot \vec{c}= \begin{bmatrix} (a_xb_x+a_yb_y+a_zb_z)c_x \\ (a_xb_x+a_yb_y+a_zb_z)c_y \\ (a_xb_x+a_yb_y+a_zb_z)c_z \end{bmatrix}=\begin{bmatrix} b_xc_x & b_yc_x & b_zc_x \\ b_xc_y & b_yc_y & b_zc_y \\ b_xc_z & b_yc_z & b_zc_z \end{bmatrix} \cdot \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}= \begin{bmatrix} c_x \\ c_y \\ c_z \end{bmatrix} \cdot \begin{bmatrix} b_x & b_y & b_z \\ \end{bmatrix} \cdot \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}=CB^TA \]

对于两个向量叉乘：

\[\vec{a} \times \vec{b}= \begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \\ \end{bmatrix}= \begin{bmatrix} a_y \cdot b_z -a_z \cdot b_y \\ a_z \cdot b_x -a_x \cdot b_z \\ a_x \cdot b_y -a_y \cdot b_x \\ \end{bmatrix} = \begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} b_x \\ b_y \\ b_z \\ \end{bmatrix} =A_T \cdot B \]

对于三个向量叉乘(参考Triple_product)：

\[\vec{a} \times \vec{b} \times \vec{c}=\vec{b} \cdot (\vec{a} \cdot \vec{c})-\vec{a} \cdot(\vec{b} \cdot \vec{c}) \]

推导公式

对于原点\(O\)和坐标点\(S_2,S_1\)，记：

\[\large \begin{split} \vec{s_1}=S_1-O \\ \vec{s_2}=S_2-O \end{split} \]

以\(\vec{s_1}\),\(\vec{n}\)向量构成平面not, 建立坐标系ontb ,分解原向量\(\vec{s_1}=\vec{s_n}+\vec{s_t}\)，如下图：

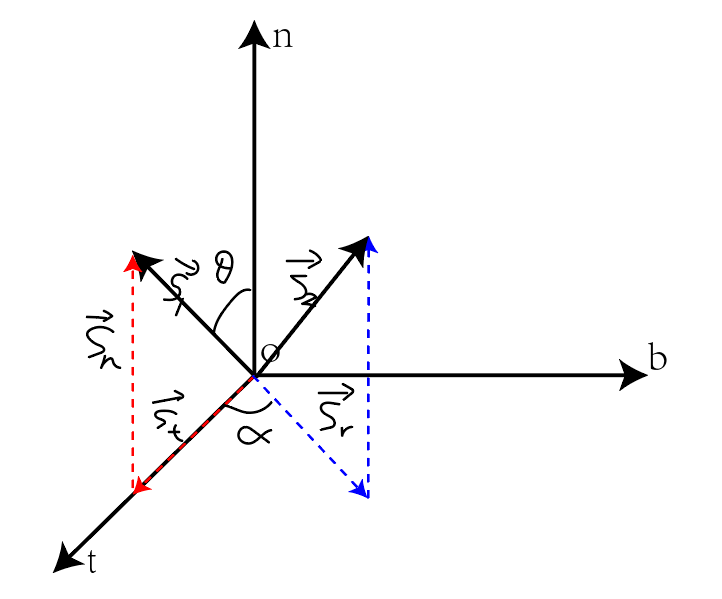
可以推导基本等式：

\[{\large \begin{align*} \begin{split} \vec{n} \times \vec{s_1} &=\vec{n} \times (\vec{s_n}+\vec{s_t})=\vec{n} \times \vec{s_n}+\vec{n} \times \vec{s_t}=\vec{n} \times \vec{s_t} \\ \vec{b} &=\frac{\vec{n}}{\left| {\vec{n}} \right| } \times \frac{\vec{s_t}}{\left| \vec{s_t} \right|} =\frac{\vec{n} \times \vec{s_t}}{\left| \vec{s_t} \right|} \\ \vec{t} &=\vec{b} \times \vec{n}=\frac{\vec{n} \times \vec{s_t}}{\left| \vec{s_t} \right|} \times \vec{n} \end{split} \end{align*} } \]

绕轴线\(\vec{n}\)旋转\(\alpha\)度之后向量\(\vec{s_2}=\vec{s_n}+\vec{s_r}\)， 其中\(\vec{s_r}\)为\(\vec{s_t}\)绕旋转\(\alpha\)度（即$ \left| \vec{s_r} \right| = \left| \vec{s_t} \right| $）

\[{\large \begin{align*} \begin{split} \vec{s_n} &= \left| \vec{s_1} \right| \cdot cos(\theta) \cdot \vec{n}= \frac{\vec{s_1} \cdot \vec{n}}{\left| \vec{n} \right|} \cdot \vec{n}= \vec{s_1} \cdot \vec{n} \cdot \vec{n} \\ \vec{s_r} &= \left| \vec{s_r} \right| \cdot cos(\alpha) \cdot \vec{t}+\left| \vec{s_r} \right| \cdot sin(\alpha) \cdot \vec{b}\\ \large &= \left| \vec{s_t} \right| \cdot cos(\alpha) \cdot \vec{t}+\left| \vec{s_t} \right| \cdot sin(\alpha) \cdot \vec{b} \\ \large &=\left| \vec{s_t} \right| \cdot cos(\alpha) \cdot \frac{\vec{n} \times \vec{s_t}}{\left| \vec{s_t} \right|} \times \vec{n}+\left| \vec{s_t} \right| \cdot sin(\alpha) \cdot \frac{\vec{n} \times \vec{s_t}}{\left| \vec{s_t} \right|} \\ \large &= cos(\alpha) \cdot\vec{n} \times \vec{s_t} \times \vec{n}+ sin(\alpha) \cdot \vec{n} \times \vec{s_t} \\ \large &= cos(\alpha) \cdot\vec{n} \times \vec{s_1} \times \vec{n}+ sin(\alpha) \cdot \vec{n} \times \vec{s_1} \\ \large &=cos(\alpha) \cdot(\vec{s_1} \cdot(\vec{n} \cdot \vec{n})-\vec{n} \cdot(\vec{s} \cdot \vec{n}))+ sin(\alpha) \cdot \vec{n} \times \vec{s_1} \\ \large &=cos(\alpha) \cdot(\vec{s_1} -\vec{n} \cdot(\vec{s} \cdot \vec{n}))+ sin(\alpha) \cdot \vec{n} \times \vec{s_1} \\ \large &=cos(\alpha) \cdot(\vec{s_1} -\vec{s} \cdot \vec{n}\cdot \vec{n} )+ sin(\alpha) \cdot \vec{n} \times \vec{s_1} \\ \vec{s_2} &=\vec{s_n}+\vec{s_r} \\ &=\vec{s_1} \cdot \vec{n} \cdot \vec{n}+cos(\alpha) \cdot(\vec{s_1} - \vec{s} \cdot \vec{n} \cdot \vec{n})+sin(\alpha) \cdot \vec{n} \times \vec{s_1} \\ &=cos(\alpha) \cdot \vec{s_1}+(1-cos(\alpha))(\vec{s} \cdot \vec{n}\cdot \vec{n}) +sin(\alpha) \cdot \vec{n} \times \vec{s_1} \\ \end{split} \end{align*} } \]

将以上向量变换为坐标，可以得到等式：

\[\begin{align*} \begin{split} \large S_2 &=cos(\alpha) \cdot S_1+ (1-cos(\alpha))NN^TS_1+ sin(\alpha) \cdot N_TS_1\\ \large &=(cos(\alpha)I+(1-cos(\alpha))NN^T+sin(\alpha) \cdot N_T)S_1 \end{split} \end{align*} \]

故：

\[\large R(\vec{n},\alpha)=cos(\alpha)I+(1-cos(\alpha))NN^T+sin(\alpha) \cdot N_T \]